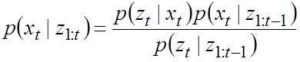Introduction
The huge genomic activity in the last century ignored the complexity and dynamical aspects associated with the homeostasis, the central concept in physiology and medicine. Emulating reductionism, major thrust was imparted to find out and rectify the singular factor associated with a disease process. Undoubtedly, this approach produces a tremendous success towards the development of modern medicine; however, it does not fulfill the expectations in terms of investments that have been made to solve different complex diseases including cancer. This actually drags the scientific community to adopt the systems approach and hence, systems biology (SB) has been accepted with great enthusiasm (Joyner & Pedersen, 2011; Ahn et al., 2006).
Though the philosophical inclination of SB has always been the goal for the biologists, however, the newer incorporation to it is quantitative statement for tracking a disease dynamics (Ahn et al., 2006; Hood 2003). In recent times, depending on the adoption of technology and analytical procedure, two prevailing approaches are being exercised by the SB community, though a third approach is also suggested by several experts of the field (O’Malley & Dupre, 2005; University of Exeter workshop report, 2006).
First one is the top-down approach. This approach identifies the contrasting features between the normal and disease, control and experimental cases at the macroscopic level first, i.e., at the organ and tissue level, then gradually identify the distinguishing characteristics at the cellular and molecular level (Katagiri, 2003; Wilson 2007). This approach is aligned with the age old discipline of Physiology (Fagan, 2004). Historically, this approach follows the foundation laid by the works of William Harvey to Claude Bernard (Dasgupta, 2002; Auffaray & Noble, 2009; Noble, 2008). Even the mathematical formulations have also been carried out by cyberneticists since 1948. The analytical models developed with some functional variables actually revealed the macroscopic behavior of the system and thereby, able to delineate the systems dynamics (Khoo, 2000).
Cancer along with the other disciplines of medicine has followed the top-down approach. This, in turn, leads to the identification of a coherent intracellular signaling pathway for the identification of cancer pathogenesis. During the last few decades the focus of cancer research is concentrated on searching the causative factors that are responsible for transformation and growth of the cancer cells along with different biomolecules involved in the process. Along with these, intercellular communication at the cancer milieu is also at the focus of interest (Dasgupta, 2002; Strange, 2005).
The second one, bottom-up approach has a philosophical notion towards the integration of low level data sets of the cellular components gradually to generate for a multicellular organism. Hence, modelling of intra- and inter-cellular pathway becomes the starting point of bottom-up approach by integrating the low level data (Liu, 2005). Once it has been formed, then only the hierarchical complexity of dynamical model generation could be expected. High-throughput technologies like, microarray and proteomics are used for data acquisition. These are able to generate the global data sets of molecular concentrations at cellular level. However, in most of the cases, analysis is done with a sharp dichotomy between disease and normal, control and experimental states (Henry, 2005; Aebersold, 2005; Church, 2005). This approach is mechanistic from the experimental sense and has the ability to identify the simultaneous relationships between multi-components. If it could be successful, it would definitely serve the objective interest towards the development of therapy at the molecular level. Hence, this approach becomes the central theme of SB venture including cancer SB. Hornberg et al., 2006 made a good review on cancer SB that actually makes an emphasis on the development of the bottom-up approach.
Bottom-up approach focuses its primary interest towards the metabolic and signaling event of a cell. So, molecular depiction of global profiling at the cell level becomes important. Hence, to fulfill its objectivity, bacterial and yeast system or the established cell lines may suffice its need. Though it is assumed that the revealed the cellular system can gradually be integrated to generate the whole system, however, in reality the phenomenon of cancer and its dynamics is represented with an isolated system. Therefore some experts believe that it is another sort of reductionism – called as “high-throughput” reductionism (Katagiri, 2003). Clinical cases are assessed through a population based analysis with one-shot data and for seeking the solution out of the global profiling of population data, pattern recognition becomes the central point of analysis. This approach would basically depict the static state of a disease and in majority of the cases conclusion about the system is drawn when it has already reached a steady state. With respect to cancer, the established relation (based on the dichotomy of state) reflects the epiphenomenon of cancer in majority of cases. Hence a group of scientists are commenting this procedure as ironic as it seeks the mechanistic explanation through heuristics (Bustin & Nolan, 2004; Weston & Hood 2004).
It is interesting to be noted here that in both the above approaches, the overall system behavior is difficult to predict. In the former top-down approaches, there is some loss of information due to disintegration of systems components. Hence, physiological entity among the different systems is lost. Due to under-defined systems’ component, the dynamical aspect of homeostasis was not in focus even in physiological research (Noble 2008), and has followed the conventional research approaches of the life science domain. Contrarily the bottom-up approach adds some assumption in the system analysis while integrating lower level to higher one (Majumder & Mukherjee, 2011).
In a very recent time a group of review articles published with the focal theme on Cancer Systems Biology covered major areas of researches in the above mentioned two aspects (Soto et al., 2011). Articles in the issue have reviewed the mathematical formulation regarding the basic understanding of the dynamical complexity of cancer development and metastasis. Here we focus to those analytical models that can be applied directly to the assessment of therapeutic dynamics in clinic, hence, emphasized on the models that deal with the clinically measured variables and the cost effectiveness (Majumder & Mukherjee, 2011).
In a very recent review article, authors have criticised regarding the clinical feasibility of the conventional top-down and bottom-up approaches under different socio-economic criteria and put another philosophical thought called “Middle-out rationalist approach (MORA)” for the assessment of the outcome of cancer therapy (Majumder & Mukherjee, 2011; Nielsen, 2012). It is needless to point out here that we cannot make any apprehention regarding the cancer development process before the clinical identification; hence, its control is beyond our limit. In this review article we focus to the different analytical approaches that can help us to make an assessment regarding the control of clinical tumors. In the next section, how the existing models help in the development of models for MORA is discussed. Section 3 discusses the advantages and prerequistes for applying MORA approch in clinic. To make an assessment in a mechanistic manner, a careful data handling is needed. Section 4 discusses on the practical procedure of data structuring for handling of clinical data and on the assessment of uncertainty in predictions. The conclusion section makes a summary of the approaches and future directions.
Multiscale Modeling
The undeniable fact is that different clinical data which are used for the assessment of the pathophysiological states of the patients are in different scales. Moreover, the applications of control and systems engineering perspectives are apprehended as a tool in the prediction of the therapeutic outcomes of a disease (Majumder 2009). To target both the aspects multiscale modeling (MSM) approach could be ideal. A considerable number of cancer models are available in several cancers with the adoption of MSM strategy.
Generalized Models
The objective interest of cancer research is to provide a strategy for the therapeutic interventions to the freely growing tumor mass. Hence, several functional variables (measured in different scales) are included in those models. Most of the models are built with clinical or experimental cases and able to validate the disease dynamics at the gross physiological level.
Models of Haematopoietic Dynamics: Cancer of haematopoietic system, considering haematopoiesis at the morphological level, forms the basis of examples discussed here. At an instant time point different cell count, multiplication rate, death rate, differentiation rate, differentiation delay have been considered as system variables – those having the properties of multiscale modeling (Colijn C, Mackey, 2005; Colijn C, Mackey, 2005b; Colijn et al., 2006; Le & Mackey, 2007). The modeling approach has the lacunae of black box modeling and is solved through the use of nonlinear mathematics. Though some molecular level data is superimposed towards the understanding of cellular behavior within gross physiological level undergoing chemotherapy (Michor et al., 2005); however, in those models relationship between the different system components across the hierarchy is not established and confined within a single system i.e., within hematopoiesis system. This modelling effort may limit to assess the drug induced behavior of other physiological systems. Therefore, with those models identification of controlling variable for therapeutic measure is difficult to predict. In a recent effort a dynamical model is developed with the cellular behavior of hematopoietic cells and describes how those cellular behaviors can be assessed in a clinical scenario. This model emphasizes the importance of initial parametric values for the assessment of future dynamics (Dhar et al., 2012).
Angiogenesis Modelling: Using theories of fluid dynamics, tumor along with its angiogenic properties are tested in a time varying system. Model curve is generated for the control of tumor growth from the experimental data with the application of different angiogenic drug to the animal tumor model. In the mathematical part, tumor growth follows Gompertzian growth characteristics. Spontaneous loss of functional vasculature, role of angiogenic signals by the tumor, contribution by the endothelial cells and inhibitory role of angiogenic drug has been considered (Hahnfeldt et al., 1999). With the theory of network flow modeling, pattern formation during the tumor growth is postulated. Chemokinesis of endothelial cells to the tumor site in response to the tumor associated factor, haptotaxis of the endothelial cells’ adhesion to the matrix tissues at the tumor site, varying capillary flow parameters and capillary radii and hence, nutrient supply to the tumor and delivery of the chemotherapeutic drug to tumor has been studied through a system of coupled nonlinear partial differential equations. Authors also simulated the effect of continuous and bolus dosing strategy in control of tumor growth. However, to implement such model, physical structure of the capillary network is essential and for clinical cases this may be difficult to track this at discrete time interval in individual patients (McDougall et al., 2012).
Gerlee and Anderson, 2011 hypothesize the mechanism of maintaining of tissue structure, called ‘structural homeostasis’ with two types of solutions. One is for tissue with high rate of cell turnover (fixed model), like colon tissue continuously exposed to mechanical stress and another is for deeper tissue where cells divide when it is needed (conservative model). Both models are based on hybrid cellular automaton model where each space is considered as cell and an empty space is filled with the growth of the neighboring cell. Cell growth is considered to be dependent on two factors – oxygen concentration and growth factors modeled through reaction diffusion equation while cell death or perturbation is imposed to it by either wound or mutation. The problem of robustness of maintenance of structural homeostasis is set with the parameterization through evolutionary algorithm. Both the models coexist in an organism and quantification of the perturbation may provide a clue to the process of cancer and/or its reversal.
Spontaneous Regression: Using cybernetics and thermodynamics, it has been possible to explain the tumor instability that ultimately causes tumor regression. Biologically, this is known as spontaneous regression of tumor. Metabolic activity of the tumor cells like oxygen tension and nutrients supply to the tumor site, temperature, and immunity has a role in the spontaneous regression of tumor growth (Dutta Majumder & Roy, 2000).
Metastasis and Cancer Invasion: Though in majority of the mathematical models, experimental data are fitted to the Gompertzian growth curve, however, they do not postulate the mechanism. Contrarily in modeling of cancer, metastasis has implications to the mechanisms of cancer growth. These models considered the delicate balance between the proteolytic enzymes and their inhibitors (Perumpanani et al., 1996), and the role of pH in the invasive process (Gatenby & Gawlinski, 1996; Sherratt, 2001). In some aspect these models can be used to understand more qualitative nature of the biological processes. For example, in breast carcinomas, tumor-associated macrophages found to be clustered distinct from vascular hot spots, has been modeled. This reveals that the macrophage clustering, an important regulator of angiogenesis might arise prior to vascularization. Thus, the condition under which prevascularization patterning arise could be determined precisely (Leek et al., 1996; Owen & Sherratt, 1997). Using traveling wave hypothesis it is argued that macrophages play an important role in angiogenesis, metastasis and tumor heterogeneity (Sherratt et al., 1999).
The “evading cell death” as a “hallmark of cancer” (Hanahan & Weinberg, 2001) is challenged in a hybrid cellular automaton (CA) model. The model considers a tumor mass having heterogeneous cells of non-cancer stem cells and cancer-stem cells, both cell types have a proliferative, apoptotic, migration capacity and symmetric division rate. The model hypothesizes that increasing the rate of apoptosis, while obviously reducing tumour size in the short-term, actually enhances growth in the long-term. The model also postulates that increasing the apoptosis rate increases the invading and metastatic potentiality of tumor cells. This capacity is further enhanced with the increase in symmetric division rate (Enderling & Hahnfeldt, 2011).
The role of tumour microenvironment plays an important role in the transition from benign or premalignant tumour to invasive cancer. Tumor growth induces stiffening to the surrounding tissue that enables them to escape an interaction with tissue macrophages and impede transport. These features are important for the transformation of benign tumor to malignant one and mimicked within the developed analytical framework. This framework is validated with the data of tumor growth in agarose gel inhomogeneities and other microenvironmental growth factors. To address the effect of signalling from stroma to tumor cells, tumor cells behavior within the tumor and the mechanical effect of tumor growth on the tumor surroundings, the framework is developed with a hybrid discrete-continuum system where former two are treated as continuum and outer proliferating layer is solved discretely with a visco-elastic description. The inner part of tumor are considered homogeneous and treated as continuum to capture the molecular, biochemical and cellular properties of cells and signalling from stroma to inner tumor is equated through reaction diffusion equation. This framework is further extended to capture the growth characteristics behavior of ductal carcinoma in situ. This work postulates that the breakdown of myoepithelial junction could be the early indicator of formation of aggressive clone and cancer progression (Kim et al., 2011). These modeling efforts give a numerous insight regarding the dynamical behavior of cancer; however, potentiality of this mathematical formulation in clinic needs to be rationalized.
Cancer Therapy
In literature several analytical models are available regarding therapeutic intervention.
Radiotherapy: Radiotherapeutic potential to colorectal cancer is evaluated in a multiscale model. Mathematical description includes the Boolean description of genetic network consisting of five genes, a discrete model of cell cycle and a fluid dynamic based continuous model for the macroscopic behavior of tumor growth and invasion. Radiotherapeutic intervention to the tumor growth is imparted at the cell cycle phase assuming proliferating cells are sensitive to the treatment. Though clinical studies have recognized p53 status as a major predictor to the response of rectal cancer to irradiation, however simulation results suggested some macroscopic factors such as auto-growth signals such as hypoxia, tumor volume and cellular overpopulation are important determinants. These factors are activated through SMAD/RAS and APC genes respectively and proliferation is inhibited through cell cycle regulation (Ribba et al., 2006). The binary descriptions of the gene activation do not provide the intermediate states of gene expression.
Immuno-Therapy: Tumor-immune cell dynamics have been investigated in several theoretical studies (Adam & Bellomo, 1997). Several authors have incorporated growth factors and modulators into models of the immune response to cancer growth (Albert et al., 1980; Adam, 1993; Kirshner & Panetta, 1998). Model has been developed to show the spatial interactions of tumor associated macrophage, normal cells and tumor cells and it has been postulated that immune cells are capable of first order removal of mutated cancer cells. When it exceeds a critical value cancer regresses (Owen & Sherratt, 1997; Sherratt & Nowak, 1992). The effect of vascularization on tumor-immune system interactions within a multicellular spheroids have also been considered (Adam, 1996), as well as a model of natural killer cell recognition of target cells based on cell adhesion and the delivery of cytotoxic hits (Kuznetsov, 1996). Fas/FasL has been investigated in a model for cytokine-modulated Th1/Th2 helper T-cell differentiation. This study showed that Fas/FasL system is an important factor in stabilizing the two polarized arms of the Th1/Th2 T helper population in response to pathogenic challenge (Yates et al., 2000). Another model has been developed to show that constitutive expression of FasL followed by secretion of FasL by the tumor cells is a potential mechanism of immune evasion. The model predicts that inhibition of matrix metalloproteinase (MMP) by means of therapeutic agent, whose activity has been demonstrated in invasive/metastatic cancer cases, causes Fas sensitive tumor cells to undergo Fas-mediated apoptosis more rapidly compared to Fas-resistant tumor cells (Webb et al., 2002). With theoretical perturbation analysis helps in revealing the bounds of the time interval of soluble Fas ligand production. It has been shown that the number of soluble Fas molecules reaches a high level when the number of membrane bound Fas is low (Webb & Sherratt, 2003).
In another attempt, a two-dimensional system of ordinary differential equations is used to characterize the basic types of phase portraits of the immune system – tumor interactions, and evaluate the role of direct in vivo (acquired and other forms of immunotherapy) and ex-vivo trained passive immunotherapy as well. The dynamics of immune system is modeled with Michaelis-Menten and sigmoid functions and showed that there are no limit cycles in the system and anti-tumor activity by tumor changes all equilibrium points from global to local ones. In the later case, the immune system has no control over the growth of large tumor, and if immunity is weak, the immune system is unable to eradicate even small tumor and provides favourable condition for tumor growth. The patterns of the asymptomatic behavior of the system do not depend on the type of stimulation function, but do depend on its parameter (Forys et al., 2006). Using the prey-predator modeling approach three species system namely, tumour cells, T-cells and macrophages are designed to evaluate the tumour stability. The work significantly proved that predation function is dependent on the ratio of tumor cell density to that of the CTL following Michaelis-Menten kinetics and in absence of active T cell tumor system exhibits unstable behavior. Incorporation of delay which is necessary for the T cell from its resting to active state causes destabilization of the tumor system (Mukhopadhyay & Bhattacharyya, 2007).
Chemotherapy: In cancer chemotherapy conventional way of assessing the efficacy of drug is evaluated through the study of pharmacokinetics (PK) and pharmacodynamics (PD). Its importance in translating to mathematical form is discussed by several authors (Derendorf & Meibohm, 1999; Dokoumetzidis et al., 2001). Different cancer chemotherapeutic drugs are administered to the body with high doses to get complete cure. However, this may produce severe toxic effect to the body due to its detrimental effect on the normal cells of the body. Thus, it is important to design treatment strategies that ensure a desired rate of tumor cell killing without producing any side effect. For this, different constraints mainly hematological parameters have been considered. Attempts have been made to optimize the drug doses by applying the PK and PD model of a specific drug (Iliadis & Barbolosi, 2000; Iliadis, 2005). Contrary to the approach it has been established mathematically that low but dose dense (metronomic chemotherapy, MCT) would be equally effective compared to the conventional maximum tolerable dosing (MTD) strategy (Mukherjee et al., 2006).
Anti-Angiogenic Therapy: Using of multiscale modeling approach with the consideration of several factors at molecular, cellular and tissue level factors correspond to in vitro tubule formation and affirm the importance of anti-VEGF or calcium blocking agent at tumor micro-environment as the ideal tumor therapeutic strategy (Scianna et al., 2011).
Comments on Multiscale Modelling
Advantages of Multi-Scale Modeling: Mapping of individual’s variation with the population behavior may blur the individual’s treatment need at different time instant. Stochastic analysis depending upon the dichotomy of state does not reveal the biological insights about the state transition process. Hence, economization of treatment cost may not be possible and in some cases patients may take unnecessary drug (Ahn et al., 2006). Contrarily multiscale modeling has the capacity to capture the individual’s parametric variations in a dynamical manner, and hence, could be applicable in a case specific manner. But it would be a mistake if we deny the population based study as the population data could guide us in the establishment of the relation between variables and thus, initialization of model building. With the initial data and/or relation, the developed model can be tested to predict the future states of an individual. The output data should be matched with the system behaviour in a dynamical state within a feasible time interval. If any deviation is observed, then corrections are needed at the parametric level. With the corrections in place, future state would be predicted again. Thus, it requires a frequent intervention and should pass through the predict-observe-correct cycle. Presently sequential data are absent in clinical or experimental cases, like toxicity data. In this direction, mathematical model can guide us to overcome those limitations.
The present challenge of MORA view is to transform different variables which are in different unit into the same meaningful platform by adjusting/calibrating them with appropriate conversion factor. For an example, it may be necessary to make a relation between blood flow rate, oxygen concentration at the tissue site from pixel data of an image (captured by magnetic resonance imaging) with microvessel diameter and number of microvessel cells for analytical assessment of cancer system. This is important to make a congruency between the formal and the natural system and combines the complexity and causal relationship of the system behavior (Wolkenhauer, 2001; Wolkenhauer & Mesarovic, 2005). Once a considerable number of dynamical tracings are available then it could reveal the dynamical behavior of the population as well.
Issues with Respect to Realistic Relevance: In bottom-up approaches there is a chance of error as in the data capturing method; it is assumed that all cells are in a homogeneous state (Wolkenhauer, 2007). Though at present time, data capturing from single cell is technically feasible, however, it loses the information of temporal dynamics. The main problem of this approach is the simultaneous incorporation of both the spatial and temporal dynamics of biomolecules. If any technology is available to monitor in in vivo state, then question arise about the data reliability while one perform the dynamics study. Capturing of sequential molecular level data is difficult and not quite cost effective (Bustin & Nolan, 2004; Weston & Hood 2004). Recently multi-scale modeling is used in bottom-up approach to reveal some important knowledge – such as, the thymic competition among T-cells during their development (Cohen & Harel, 2007). However, this ultimately reveals the knowledge at the middle zone of hierarchy.
The available models are validated with experimental results (Liu, 2005) which are basically kinetics data (Dokoumetzidis et al., 2001), though nonlinear dynamical behavior of cancer is acknowledged (Kholodenko et al., 1999; Ferrell Jr. 2002). With the presently available quantitative statement at present (i.e., data capturing procedure or the mathematical models) the phenomenon of cancer cannot be tracked beyond the in vitro procedure (Dasgupta 2002; Henry, 2005; Church, 2005; Kothari & Mehta, 1994; Kothari & Mehta, 1997; Giaever et al., 2002; Guttmacher & Collins, 2002; Chanda & Caldwell, 2003; Munson & York, 2003; Grene & Depew, 2004). If dynamics of a multicellular organism can be predicted by integration of low level data – undoubtedly cost of investigation would be enormous. Chaos theory and nonlinear dynamics revealed that minor variation in the input data (a change after the 5th or 6th position after the decimal) may produce a drastic shift in the output in the long term and minor variation in data capture may indicate a disease state (Dhar et al., 2012; Gleick, 1997; Kaplan and Glass, 1995). This becomes more pronounced with low level i.e., molecular level data while integrating these into the dynamical model. In reality there is a large variation of data in individual patient; so at theory, complexity could not be revealed by just mere adding up of components along the hierarchy. “The end point we care not the protein-protein interaction or how a cell behaves in culture”; hence, the clinical application of knowledge is not very feasible (Henry, 2005; Cohen & Harel, 2007).
Top-down approach may seem to be useful in the first place, since some information is readily available at the top (gross) level. One is provoked to use it, develop diagnostic and analytical tools and then get stuck at some point. Starting with the manageable information one has to make a huge assumption in the missing data parts of interrelations. So decent is not easy. Moreover, it may identify different component at different time dynamics (may be epiphenomenon also). Hence, combination of two approaches is also suggested (Katagiri, 2003).
MORA
As suggested earlier, adoption of middle-out rational approach (MORA) for systems biology is more pertinent for the clinical application (Majumder & Mukherjee, 2011). The bottom-up approach starts from the molecular structure and concentration of different molecular components and moves up to gross function with a hypothesis that these would be repeated at different level of hierarchy. Similarly, top-down approach starts from gross functionality (and hence gross morphology) and moves down to the molecular structure. Thus, it identifies different component at different time dynamics. MORA view is solely concerned with the function; however, for tracking the systems, some variables are important. Hence, it considers only clinically relevant variables for a disease process and in turn, works with few or a number of systems components. This procedure is in contrast to the bottom-up approach but allied with the top-down approach. The selected data may be from different levels of hierarchy hence, may be of molecular, cellular or tissue level data. However, in contrast to the top-down approach these selective data can intermingle with the physiological function in a dynamic manner. The selected data in MORA approach are subjected to multiple inputs to a system and multiple outputs from that system are different functions of the system. The feedback or relational interaction between different variables, if imposed into the system is on the basis of experimentally established relationship (hence, variables are quantifiable data). MORA view is accepting and applying any knowledge that has the realistic relevance.
Models Developed with MORA
Attempt has been made across the systems to consider the pathophysiological constraints in cancer. Heterogeneous tumor system, drug application system, immune system, excretory system and metabolic system, thus, toxicity development – both drug induced and tumor induced have been taken into consideration. Tumor system is consisting of two types of cells – drug resistant and drug sensitive types of cells with respect to a particular chemotherapeutic drug. Each cell type has been considered with different doubling time – growth of the resistant cell type being more than that of sensitive type and different conversion rate between the cell types. Application of drug is considered as the external forcing function that inhibits the growth of the tumor system. Immunity related cell killing has been shown to be advantageous in MCT strategy as it may provide further controllability to the tumour system. With this model rigorous simulations have been done to test the differences between the free growing tumor system and the tumor system under the condition of different chemotherapeutic strategy viz., the conventional maximum tolerable dosing and metronomic chemotherapeutic dosing strategy together with different combinations of multiple drugs, immunotherapy and anti-angiogenic therapy by using anti-VEGF– may be considered separately or all are lumped together as the subtractive term with respect to the total tumour load at a discrete time interval (Mukherjee et al., 2006).
Due to unavailability of discrete data sets of toxicity (at different time interval) in literature, the issue of toxicity is solved through Fuzzy logic based analytical approach. Development of toxicity during the treatment provides feedback to the consecutive drug application decision. It has been hypothesized that MCT will not impose much extra burden (toxicity) on the physiological system though it has been applied for a long time, and if, there is any delay of drug application in MCT due to the pathophysiological constraint (accumulation of toxic metabolites of tumour cells itself or its debris due to its death), MCT still has a better control over the tumour system (Majumder & Mukherjee, 2006a). The delay in drug application has been determined and is governed by the clearance rate of toxicity through the excretory system. With higher clearance rate, delay in consecutive drug application is reduced (Majumder & Mukherjee, 2006b). The threshold of toxicity is another determinant factor for the clearance (Majumder & Mukherjee, 2007). However, retention of drug within the physiological system has an advantage of an extra cell killing efficiency (Mukherjee & Majumder, 2008). Thus, realistically controllability of tumour growth is governed by the dialectical relationship of the patho-physiological constraints and the presence of drug under the condition.
Due to unavailability of sequential clinical data in literature, the model is based on the strong relational aspects under the condition of malignancy and considers the physiological system as an entity. However, it appreciates the data from different levels of information. Implementation of the model relies on different molecular, cellular or functional physiological procedures for the procurement of data. Tumor volume can be identified from the MRI analysis (physiological level data). Identification of cell types (molecular level data), multiplication rate of tumor cells, drug sensitivity can be identified by biopsy followed by in vitro culture (cellular level data). Presence of drug within the system, clearance rate of the drug can be obtained from the information of the amount of administered drug and presence of drug metabolite excreted through urine (biochemical or molecular level data). Amount of metabolite in the discrete time interval as well as clearance rate of the metabolite can be obtained from the measurement of different blood and urinary biochemical parameters like urea, creatine and creatinine (Mukherjee et al., 2006; Majumder & Mukherjee, 2006a; Majumder & Mukherjee, 2006b; Majumder & Mukherjee, 2007; Mukherjee & Majumder, 2008).
In another effort models for tumor growth and invasion based on multiscale modeling has been developed employing selective variables (which are measured in different scales) across the different levels of hierarchy of the physiological system. Such variables are densities of tumor cells, proliferation and apoptotic rate of the cells, concentrations of vital nutrients, different cytokine concentrations such as VEGF, fibronectin (FNT), and tissue mettaloproteinase concentration at the cancer milieu and describe the cells’ collective migration and evolving neovasulature. These input variables are integrated in a nonlinear system using multi-grid points to represent the 3D morphology of tumor shape. As different empirically based observations reveal the growth characteristics of tumor; so this sorts of model has the capacity to correlate the molecular characteristics to morphological representations. Simulations with these models have been done with different in vivo cell line and ex-vivo patients data. The simulated results represent different clinical and experimental autopsied data. However, considerations of energy formulation that accounts for different mechanical forces e.g., the cell-cell, cell-matrix adhesion, elastic effects may limit its clinical implications while tracking the system undergoing any therapeutic scheduling. It is worthwhile to mention that in majority of the clinical cases patients appear with the developed tumor (Frieboes et al., 2007; Wise et al., 2008; Bearer et al., 2009; Cristini et al., 2009; Macklin et al., 2009). For tracking the tumor system during therapy it is necessary to develop model that could match with clinical scenario. Hence, models have been developed with reduced number of grid points in a 2D matrix to check the probabilistic movement of cells. Reduction in number of grid points has the advantage of tracking the system through CT scan followed by biopsy procedure. Through the same model relationship between microvessel growth and growth of tumor cells are established. This model also the relationship between the tumor growth, TAF (tumor associated factor) and fibronectin (FNT) concentrations; and makes a provision for the quantitative assessment of TAF concentration from peripheral blood, Thus allows an apprehension regarding the in vivo tumor growth dynamics from peripheral blood concentration of TAF (Bhattacharya & Majumder, 2009; Majumder, 2010). However, with this modeling approach, initial parametric settings may be difficult as the modeling variables are not suitable with the biopsy examination where tumor cell number along with the microvascular density can be measured with more precision. Therefore, another modeling approach has been done where growth of tumor cells are linked with the number of microvasculature cells (Mukherjee & Majumder, 2010).
Characteristics of MORA View
MORA has the power to intermingle the relational aspect, measurement technology, knowledge and analytical methods to get a better estimation. Application of linear state equations with conditional feedback system would be better suited to establish the dialectical and co-ordinated relationships between multiple variables, assessment of multiple therapeutics and its side-effects, day-to-day (time varying) monitoring and analysis (intermittent monitoring), nonlinear dynamical behaviour of the physiological system, switching decision between different drugs at individual level and the systems boundary condition. Boundary conditions reveal the system’s anticipatory behaviour (Wolkenhauer, 2001; Majumder & Mukherjee, 2007, Mukherjee & Majumder, 2008). This in turn would be able to encompass the limitations of the measuring instruments and avoid the unnecessary cost in measurement.
Systems’ Entity: This approach considers the physiological system as an entity. This is at par with the age old definition of the biological system (Munson & York, 2003; Grene & Depew, 2004). With this, systems hierarchy and functions can be adopted in a coordinated manner.
Incorporation of Isolated Observations: Contrary to other views, MORA view gives an emphasis on three aspects: the dynamical behavior of life processes, the hierarchical complexity of living organism, and epistemological and historical evidences. This can help in understanding the functioning of living system with a low cost. Thus, isolated observation can be tested by incorporation as a component of the difference equation. This also makes a provision of synergistic application of experimental and observational findings.
Qualitative Aspects: Present era of ascendancy in the clinical trials is indeed an era of numerical/statistical reasoning and such mechanistic/deterministic reasoning “leads to theoretical dogma. Evidence based clinical trials seems to make systematic over-simplification.” This, in turn, makes restriction to the clinicians’ ability to tailor a treatment strategy according to the need of an individual and reinforces them to adopt “pre-formulated therapy”. “In clinical practice, many oncologists believe that patients’ interest can be better served by good traditional observational studies and many physiological parameters can be judged with a qualitative approach” (Dasgupta, 2002; Wolkenhauer, 2007). MORA provides the rationality with mathematical basis to encompass all these aspects. The qualitative aspects can be handled through the use of fuzzy logic.
Reductionism: Considering the mathematical feasibility, it is quite difficult to remove the reductionism absolutely as, large model may have an unavoidable consequence with respect to the prediction of a therapeutic outcome. It is important to stress that “the objective of mathematical modeling work is not to generate a large scale computer simulation of a biological process say, metastasis; although such model is feasible in principle, its complexity would make it so sensitive to underlying assumptions as to be of no practical value. It is true that the most effective model has a smaller number of variables” (Sherratt, 2001). Hence, in Systems Medicine the judicious choices of variables is important and it is unnecessary to go for the high-throughput data. Moreover, MORA view tries to solve the human health related problem at the individual level with reduced treatment costs; hence, it is important to track the system behaviour with reduced dimension. By the term ‘reductionism’ concerned community want to refer to the approach of molecule centric determinism.
Assessment of Drug Efficacy: As this approach considers the pathophysiological constraints of individual, efficacy of drug can be assessed at the individual level. This approach may provide the opportunity of reassessing the existing drugs (therapeutic scheduling) and toxicity assessment. Design and modification of therapy with the available drugs at the individual level is another challenge to the systems biologists and should not be overlooked. This is in contrast to the approach of looking for new drug. This also provides the methodology to the pre-clinical pharmacological assessment and clinical trials (Henry, 2003; Majumder & Mukherjee, 2007) or post-clinical care scheduling in different diseases including cancer.
Validation
Still, the models based on MORA view (Mukherjee et al., 2006; Mukherjee & Majumder, 2006a; Majumder & Mukherjee, 2006b; Majumder & Mukherjee, 2007; Mukherjee & Majumder, 2008; Bhattacharya & Majumder, 2009; Majumder, 2010; Mukherjee & Majumder, 2010) have not been tested or validated with clinical cases in a dynamical sense. However, the models developed so far with the MORA view are based on established relational behavior and all parametric values are expressed in percentage with respect to normal population. Hence, the model has the flexibility to fit to the individual cases. Moreover, as the models use difference equations, hence, there are scopes to incorporate extra information, if needed. Different biological conditions can be implemented through conditional feedback. This provides extra flexibility to simulate the complexity and nonlinear behaviour of the system under the condition of malignancy (Wolkenhauer & Mesarovic, 2005; Wolkenhauer, 2007), 90 (Skogestad and Postlethwaite, 2005).
Generally clinical medicine is come to the way after animal testing and previously analytical models cannot be accepted until it is evident with the (animal) experimental data; however, with the objections raised by different animal ethical committee across the globe restrict the use of animal for biological experimentations (Times of India, 2012; Humane Society, 2011; Report from the Commission to the European Parliament, 2011). Undoubtedly for implementing or testing of an analytical model in animal model requires huge number of animal sacrifice. This should force the scientific community to think or emphasize on the biological domain knowledge rather blind animal experimentations in the name of validation, more specifically the clinical relevance of the biological rationality. SB community is now acknowledging the importance of mathematical/analytical model based with rationality (Wolkenhauer et al., 2009).
In a recent effort it has been shown the implementation can be done by altering the calibration of parametric data of the variables of mathematical model (though the model does not consider the hierarchical systems level complexity) with different individual clinical cases of leukemia patients (Michor et al., 2005). We hope in that manner models generated by MORA view could be successful in the clinic scenario. In a recent effort, such modeling scheme is clinically aligned to accommodate morphological data and phenomenological characteristics of the hematopoietic system, thereby different hematological diseases can be assessed with a cost effective manner (Dhar et al., 2012).
Management of Clinical Data for Models with MORA
Like other branches of medicine, cancer treatment should be governed by evidence based decision. Considering physiological homeostasis in a dynamical sense (Noble, 2008), evidence can be sought through in a different way rather than statistical inference. It is needless to point out here that cancer treatment is a prolonged process, and has variations of different variables at the individual level. This may lead to a state of indecision. So, various data from different levels of physiological hierarchy in different individuals should be tested through the dynamical model. At present moment, different researchers have proposed different models for tumor dynamics and cancer treatment. So there is an immense need for the development of a systematic approach for the understanding of the feasibility of different analytical models and decision-making. In the arena of SB, different approaches exist; however, each does not encompass all aspects. Moreover, there is unavailability of enough data sets. This augment is for the indecision towards a successful therapy planning (Baker & Kramer, 2011). Contrarily MORA view accepts any of the views if it is clinically aligned. Hence to implement the MORA view, data structuring needs to be modified/developed.
Decision Support System
A Decision Support System (DSS) is definitely a better approach, and, can provide oncologist a package through which they can get useful suggestion and helpful information to decide a treatment strategy. A DSS is an interactive, computerized information system designed to help decision makers, by providing useful information (compiled from raw data) and helpful suggestions. A DSS to aid cancer treatment may provide information about patients’ patho-physiological condition stored in different stage of treatment. It may also provide suggestion about future treatment. With the stored pathophysiological data and input of the effect of drug is required for providing suggestion.
Number of works done by researchers previously, explains the mechanism of tumor initiation, tumor progression and long term consequences of anti-angiogenenic therapeutic regime have been explored (McDougall et al., 2006; Chaplain et al., 2006; Cristini et al., 2009). The importance of mathematical models in cancer development can be found in a latest review (Byrne, 2010). Similarly, with the application of MORA view, as described earlier, the effectiveness of MCT (another type of anti-angiogenic therapy) in comparison to MTD is evaluated analytically in a number of works (Mukherjee et al., 2006; Majumder & Mukherjee, 2006a; Majumder & Mukherjee, 2006b; Majumder & Mukherjee, 2007; Mukherjee & Majumder, 2008; Bhattacharya & Majumder, 2009; Majumder, 2010). To get a benefit out of the models developed with MORA view, development of a proper DSS is needed.
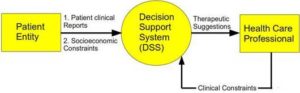
Figure 1: Context Diagram of the System
System analysis needs to be conducted for developing a DSS. A Data Flow Diagram (DFD) approach has been adopted to explain the system analysis. Main challenge in providing such an idea is to capture the data flow among various processes and providing suggestion to the Health Care Personnel (HCP) with the aid of such data. Naive approach of providing HCP with helpful information may be to maintain a large database of patient’s clinical investigation reports. However, that alone will not suffice. Primary approach should be to provide helpful suggestion to HCP for further treatment. The Context Diagram (CD) shows the overall view of the system (Figure 1). This involves a single process and two entities. In the level – 1 DFD, processes and data flow between them are expressed. Seven major processes have been identified for the system as shown in Figure 2.
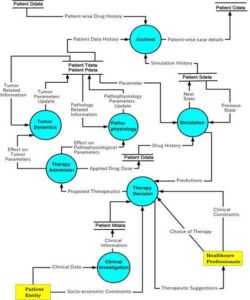
Figure 2: Level 1 Data Flow Diagram of the System
Careful design of such a system will help in long-term treatment of cancer by providing support to HCP and also can bring transparency in the entire treatment process. In the developing countries, where socioeconomic constraints prevent people suffering from cancer to undergo proper treatment, a DSS like the one described above can be a helpful tool to systematically manage the treatment of cancer to reduce the cost. Uncertainty may be handled by introducing a separate process of stochastic filtering. Implementation would mean calibration with respect to real scenarios.
System Requirement and Feasibility
Depending upon the characteristics, DSS may be of various types. Most basic DSS may be a Data analysis system which only provides useful data for decision making. It is the duty of the decision maker to decide about the relevance of the data. DSS may be improved further to extract information needed for decision, but the decision maker has to compare against expectations. Next level of DSS, called The Representation model, can be designed to define expected behavior of a system and compare this to actual one. Further improvement to representation model gives the Optimization model which uses the variations to decide on actions that can optimize future behavior.
The proposed system captures the patho-physiological data at different instants of time and does the necessary quantitative conversions so that the information fits into the model of simulation. Simulation models are based on the literature available on the mathematical models of various aspects of cancer system; like molecular, patho-physiological, biochemical and therapeutics. Depending on the analytical merits of such system models; the simulation results can predict about short-term outcomes of applying certain treatment strategy. Those possibilities in turn may be referred / considered by HCP before administering actual therapy.
Though the models are capable of long-term predictions as well, because of mis-modelling and uncertainties in initial conditions, the error in prediction would grow. The availability of fresh raw data of patient can reduce the growth of error by way of replenishing the initial conditions from time to time. This concept is similar to weather prediction system, where the weather prediction model is run using available short-term system data and initial conditions are replenished accordingly when new measurement is available. Actually, these systems are highly time varying and non – linear in nature, and, therefore sensitive to the initial conditions.
System requirement may also include archival of case studies for patients, so that it becomes useful for the overall progress in health care research. Discussion in preceding sections has established that, it is very much essential to keep records of pathophysiological condition of patients from time to time. Also, HCP tries to assess qualitatively the status of the tumor, for which, they consults patient pathological reports. Computer storage capacity and speed of computation is increasing day by day and also hospitals and clinics are maintaining such treatment details for patients nowadays. So, from that point it is feasible to design such DSS for cancer treatment management.
Proposed System Design
This section describes of the specifications of both the data storage and processes shown in the DFD (Figure 2).
Data storage specifications: storage Patient-Tdata % stores tumor information
{Patient_id, %unique-id for each patient
Time_instant; % sequential time
Cell_types; % identified variety of tumor cell types
mul_rate; % multiplication rate of each tumor cell types
Mut_rate; % mutation rate or conversion rate between the tumor cell types
T_others; % other parameters if any}
Storage Patient-PData %stores patho-physiological information
{Patient_id, time_instant;
Immu_stat; % qualitative, stored as percentage relative to normal population
Tox_lev; % qualitative, stored as percentage relative to normal population
Vasculature_count; % count of vasculature cell
Socio_economic_grade; % qualitative, gradation used to judge feasibility of therapy}
Storage Patient-MData % stores clinical investigation (measured) information
{Patient_id, time_instant; % some data are captured once while some are at different instant of time
Morphological_stage; %qualitative grade of the patient
Biopsy_data; % qualitative, tumor grade (clinical / pathological)
Bio-chemical_data; % blood/urine analysis biochemical parameters expressed in units/litre
Radio_diagnostics; % qualitative, anatomical localization of tumor
Tumour_load; expressed in terms of volume as obtained from radio-diagnostic data
Immunological_data; % immunological status expressed in terms of normal population
Molecular_data1; % mutational information in change in base pair
Molecular_expression; % gene expression profiling in terms of pixcel }
Storage Patient-Ddata % stores drug treatment information
{Patient_id,
Date_of_therapy;
Type_of_therapy % chemodrug – MTD/MCT, Immunomodulatory drug, anti-angiogenic drug, other drug
Drug_type; % generic name of drug
Drug_sensitivity; % tumor cell sensitivity
Drug_dosage; % in units / body surface area or per kg. Body weight
Outcome_therapy % narration based}
To maintain the simulation status of the patient, a data store named Patient_Sdata is used. This basically stores the outcome of simulating different treatment strategies at any given point of time. The comparative assessment of these outcomes is passed on for decision on the therapeutic strategy to be adopted. Details are given in next section where simulation is described as a process in the system.
Combining these data stores, a case history can be generated for the patient. Some basic archival related fields may be maintained. Initial tumour stage, treatment result etc may be summarized. This data store is named as Patient_Cdata in the DFD. Details are described in Archival process.
Process Specifications: The entire system may be implemented by using six processes. Following is the brief overview of the processes that may be used in the desired system.
Process: Simulation – Based on the information received from patient’s current condition and patient’s drug profile data store, simulation suggests treatment strategy to physicians. It accesses patient’s present tumor and pathological condition from Patient data storage, compare with previous conditions, consult the drug history and provide suggestions for further treatment. At the same time, it also keeps track of simulation by updating simulation status. The present model uses a simple difference equation as follows:
x(k + 1) = Fx(k) + Hu(k) —————— (1)
Here, x(k) represents a vector consisting of cell count of different cell types at instant k. Cell types in a tumour are different in the way they respond to the treatment. Some cell types resist the applied drug while some are highly sensitive to the drug. Cell types have different growth rates, different death rates and are inter-convertible through mutation. These properties of cell types are represented through the state transition matrix F. F may become time-varying and in that case will be represented as F(k). Here u(k) represents the drug applied to the system at the instant k. H represents the translation of drug to the cell count. Employing the concept of negative state feedback, the amount of drug is connected to the number of cells killed. Then, we have,
u(k) = −Kx(k) ——————————– (2)
Then, the new F matrix becomes (F −HK) and the tumour dynamics would now depend on the Eigenvalues of (F −HK) rather than F. The values of H and K would come from the administer_ therapy process.
Process: Patho-Physiology – The patho-physiology process get its input from the administer therapy process. This process basically describes the effect of applying drug on the patient. It has been proved that some types of drug are very much effective in killing tumour; but may alter the patho-physiological condition of the patient drastically (Mukherjee et al., 2006; Majumder & Mukherjee, 2006a). The patho physiology process should monitor the present patho-physiological condition of the patient, and should alert the system in case of any danger. Depending on the alert of this process, system may respond by giving some therapy decision (such as: enhanced the clearance rate). For the simulation of this process, mathematical model described in the work done of Majumder & Mukherjee, 2006a can be used. This process contributes in updating patients’ pathophysiology status by updating parameters describing immune status, vessel parameters, kidney conditions etc.
Process: Tumour Dynamics – The tumour dynamics update the tumour related data of the patient. Tumour related data basically consists of the cell count for different cell types in the tumour. The concerned parameters are also maintained here. It receives therapeutic information from the administer therapy process. It access database for related previous data. By running mathematical model for the dynamics of tumour, it updates the patients’ tumor statistics. The parameters used in prediction process, namely, F, H, K etc. are maintained by this process.
Process: Therapy Decision – The therapy decision takes therapeutic suggestions from simulation and propose therapy to the administer therapy process. For applying of chemotherapy, a number of constraints such as risks of applying chemotherapy to patient need to be considered in this stage (Repetto, 2003). For that, it helps the doctor entity by providing the details of therapeutic suggestion. It also takes into account the socio-economic constraints of the patient entity. If the suggestion provided by prediction process does not violate any clinical or socioeconomic constraints,therapy decision propose the suggestion to administer therapy process. Considering various constraints, therapy decision may take some of the following decisions:
- Can arrange for immune boosting.
- Determine chemotherapy dose.
- Suggest anti-angiogenic therapy.
- Suggest surgery in case of high tumour load.
Physician may suggest any combination of the above mentioned strategies.
Process: Administer Therapy – It receives a therapy proposal from the therapy decision. It then applies this proposal and passes on to tumour dynamics and pathophysiology. It also updates the drug profile of the patient. The modelled system dynamics updates to next state based on this admisistered dose. This serves as initial condition for next iteration, unless fresh patient data is captured.
Process: Archival – Process archival collects information from Patient_Xdata (where X=T, S, D, P), data storage, process them and archive to Patient_Cdata storage. It is basically a collection of various case studies. It is designed to extract essential information regarding patient treatment easily. It is not necessary to archive treatment information regularly. Only control points need to be stored where the treatment strategy is changed. The archival process determines the control points based on the date field of the drug profile. It then determines the duration of the treatment and updates the time range. This process continues while a patient is within the system.
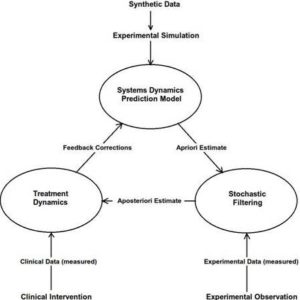
Figure 3: Scheme to Handle Uncertainty
Handling of Uncertainties
Measurement of all system variables is not feasible. Variables for which measurement is possible can be invasive or non-invasive. Invasive methods cannot be applied too frequently. Often non-invasive methods are approximations or indirect measurement, leading to bias and errors contaminated with random noise. Thus, the system observation in continuous mode is mostly not possible. Under such circumstances, we need to rely on predictions based on extrapolation in terms of system models to study system behaviour at all arbitrary time instances.
System models are basically obtained as differential equations describing the rate of change of chosen system variables with time. One can discretize from the continuous domain as well and this is particularly suited to computer based control environment. Such system models are able to predict the system behaviour at arbitrary time steps if all variables are properly initialized. But accurate predictions depend on knowledge about system equations, the system parameters in particular. Since there is continuous random perturbation of the operating environment, there is uncertainty associated with the estimation based on the system model.
In reality, if the system is initialized with reasonable accuracy, the system model can be applied to obtain an apriori estimate of the variables. The error of such estimate with respect to the true system state can be assumed to be a random vector variable with zero mean and a covariance matrix resembling the process noise for linear time invariant systems with additive white Gaussian noise. Now, a small (linear) combination of the system variables is measurable and the measurement vector is again noise contaminated. Preferably the noise model is assumed to be additive white Gaussian. When these noise covariance matrices can be specified and modelled, one can design a stochastic filter, called Kalman filter that removes the noise and generates aposteriori estimate closer to the true value of the state vector (Technical Staff, Analytic Sciences Corporation, 2001; Grewal & Andrews, 1993; Brown & Hwang, 1997).
Increasing the number of measurements improves the aposterior distribution resulting in a sharper peak closer to the true parameter. In absence of adequate measurements, proper system modelling can play a role in refining the estimation (Figure 3).
The theory of stochastic filters originate from Bayes theorem which uses maximum likelihood principle and a generic name Bayesian filter is used to designate such algorithms (Candy, 2009). The time update equations can be used to update the system states at desired time intervals. Depending on the uncertainty associated with the knowledge of system dynamics, the estimated or updated state vector spreads in an uncertain zone around the true value. Available measurement at that time point follows another distribution around the true value. Then the state estimation problem becomes one of maximum likelihood estimation with the apriori estimate following a Gaussian (or some other) probability distribution and the measurement providing a conditional probability around it to formulate the aposteriori estimate.
The model works out the conditional probability of state variables at a given time instant given the measurements available from previous time instants. This probability in turn depends on a system model that connects the state variables from previous to present time instant apart from the measurements. The conditional probabilities are updated following the Bayes’ theorem. We describe below the Bayesian filtering equations:
Predict:
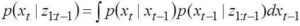
Update:
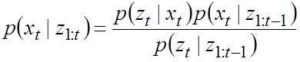
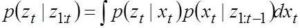
The generic stochastic filtering approach presented here has high computational complexity. The popular engineering approach in this regard has been to use Kalman filter. Kalman filter actually follows the Bayesian concept with the assumption that the error of both process and measurement (with respect to the truth value) follows zero mean white Gaussian noise. Then the propagation of error of the aposteriori estimate with respect to the true value will follow zero mean and a variance that is less than both process and measurement noise covariances. The filter is said to have converged when this error covariance gets close to zero.
However, for nonlinear systems and also wherever the assumptions of white Gaussian noise cannot be applied, more generalized Bayesian filtering algorithm has to be designed. Such filters are named particle filters, where a number of instances (called particles) are generated during each time update, before blending the result with measurement updates (Arulampalam et al., 2002). During each iteration, the particles that survive resemble more closely the true system dynamics at that instant. These filters basically use multiple models and adapt to the closest system at any time instant. This concept of multiple model adaptive estimation (MMAE) is expected to give very good results with biological systems which are difficult to model. Such an exercise of MMAE calls for much higher amount of computational resources (Hanlon & Maybeck, 2000; Hanlon & Maybeck, 2000b).
Conclusion
Bottom-up approach relies on the short time span confined experimental evidence/observation with an assumption of homogeneity of biological system. Hence it ignores the spatio-temporal dynamical information. At the analytical level, they depend on the population based data and statistical tools and at the application front the approach is deterministic. Top-down deals with lesser number of elements and hence identify different element at different time points which may be the epiphenomenon of cancer at different time points. The ultimate focus of this approach at the therapeutic front also leads to determinism.
Contrary to other views of SB, MORA view appreciates the nonlinear dynamical, dialectical and relational behavior among the components of living system and considers the realistic relevance of control. The ever-increasing restrictions that are being imposed on animal experimentations may necessitates the scientific community to think on the rational basis of an analytical model rather than the conventional validation process ground with the snap shot data from an animal experimentation. Therefore, the pendant understanding of a system behavior is leading to start the development of the model with the established inter-relationship between different components of a system and those should be in measurable scales. This approach in turn, helps in prediction about the future state from the model. However, refinement of the model could be done by observations from the reality followed by corrections in parametric values to get a better prediction. Hence a combinatorial intervention is the major ingredient of MORA approach. This would, in turn, help to provide a better understanding about the disease dynamics with a more quantitative statement.
In doing so, multi-scale modeling approach could be the ideal. The advantage of the approach is that (clinical) variables measured in different scales can be incorporated into systems equation. Moreover, qualitative assessment which is still being regarded as the major component in the clinical practice – for the understanding of the well-being of a patient and thereby the quality of life assessment, can be incorporated into systems equations and hence can be judged through the application of multi-scale modeling approach. The another advantage of multi-scale modeling approach is that if any other factor that may be missed out in the presently developed analytical model can be incorporated in future; so that, there is a provision of further refinement of the existing model. Therefore, the implications of multi-scale modeling in SB, particularly in Systems Medicine is undeniable. As far as cancer is concerned, especially in understanding and predicting of the future states or outcome of a therapy, multi-scale modeling methodology is a very powerful approach, however, considering the rationality it should be propelled through domain knowledge.
The information system analysis presented here can handle the complexity of decision support system required for cancer patients. However, the designed system can be successfully implemented only if the data input is clean. Hence, uncertainty handling has to be an integral component of any software designed for providing decision support to the clinicians. This includes absence of data points as well as noise in measured data. The nonlinear nature of systems dynamics makes it difficult to predict systems outcomes in long term but nevertheless measurement taken from time to time gives important replenishment and reduces error in prediction. These features need to be further strengthened so that its relevance in systems biology/medicine is needed to be established firmly.
Conflict of Interest
Authors declare there is no conflict of interest.
(adsbygoogle = window.adsbygoogle || []).push({});
References
Adam, J. A. (1993). “The Dynamics of Growth Factor-Modified Immune Response to Cancer Growth: One Dimensional Models,” Mathematical & Computational Modelling 17: 83-106.
Publisher – Google Scholar
Adam, J. A. (1996). “The Effects of Vascularization on Lymphocyte-Tumor Cell Dynamics: Qualitative Features,” Mathematical Computational Modelling 23:1-10.
Publisher – Google Scholar
Adam, J. A. & Bellomo, N. (1997). A Survey of Models for Tumor-Immune System Dynamics. Birkhäuser, Boston.
Publisher – Google Scholar
Aebersold, R. (2005). “Molecular Systems Biology: A New Journal for New Biology?,” Molecular Systems Biology 1(Editorial):2005.0005.
Publisher – Google Scholar
Ahn, A. C., Tewari, M., Poon, C. S. & Phillips, R. S. (2006). “The Limits of Reductionism in Medicine: Could Systems Biology Offer an Alternative?,” Plos Medicine 3:709-713.
Publisher – Google Scholar
Albert, A., Freedman, M. & Perelson, A. S. (1980). “Tumors and the Immune System: The Effects of a Tumor Growth Modulator,” Mathematical Bioscience 50:25-58.
Publisher – Google Scholar
Arulampalam, M. S., Maskell, S., Gordon, N. & Clapp, T. (2002). “A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking,” IEEE Transaction of Signal Processing 50(2): 174–188.
Publisher – Google Scholar
Auffray, C. & Noble, D. (2009). “Origin of Systems Biology in William Harvey’s Masterpiece on the Movement of Heart and Blood in the Animals,” International Journal of Molecular Science 10: 1658-1669.
Publisher – Google Scholar
Baker, S. G. & Kramer, B. S. (2011). “Systems Biology and Cancer: Promises and Perils,” Progress in Biophysics & Molecular Biology 106: 410-413.
Publisher – Google Scholar
Bearer, E. L., Lowengrub, J. S., Frieboes, H. B., Chuang, Y.- L., Jin, F., Wise, S. M., Ferrari, M., Agus, D. B. & Cristini, V. (2009). “Multiparameter Computational Modeling of Tumor Invasion,” Mathematical Oncology 69:4493-4501.
Publisher – Google Scholar
Bhattacharya, S. & Majumder, D. (2009). “An Analytical Approach for Tracking the Tumor Systems Dynamics,” IEEE Proceedings of World Congress of Nature & Biologically Inspired Comptuting, (2009), Pp. 92-97, IEEE Catalogue No. CFP0995H-CDR, ISBN: 978-1-4244-5612-3, Library of Congress: 2009907135.
Publisher – Google Scholar
Brown, R. G. & Hwang, P. Y. C. (1997). ‘Introduction to Random Signals and Applied Kalman Filtering,’ John Wiley and Sons, New York, Canada.
Google Scholar
Bustin, S. A. & Nolan, T. (2004). “Pitfalls of Quantitative Real-Time Reverse-Transcription Polymerase Chain Reaction,” Journal of Biomolecular Techniques 15:155-166.
Publisher – Google Scholar
Byrne, H. M. (2010). “Dissecting Cancer through Mathematics: From the Cell to the Animal Model,” Nature Reviews Cancer 10: 221-230.
Publisher – Google Scholar
Candy, J. V. (2009). Bayesian Signal Processing: Classical, Modern and Particle Filtering Methods, John Wiley and Sons and IEEE, Hoboken, New-Jersey, Canada.
Publisher – Google Scholar
Chanda, S. K. & Caldwell, J. S. (2003). “Fulfilling the Promise: Drug Discovery in the Post-Genomic Era,” Drug Discovery Today 8:168-174.
Publisher – Google Scholar
Chaplain, M. A. J., Mcdougall, S. R. & Anderson, A. R. A. (2006). “Mathematical Modeling of Tumor-Induced Angiogenesis,” Annual Review of Biomedical Engineering 8: 233-257.
Publisher – Google Scholar
Church, G. M. (2005). “From Systems Biology to Synthetic Biology,” Molecular Systems Biology 1(Editorial):2005.0032.
Publisher – Google Scholar
Cohen, I. R. & Harel, D. (2007). “Explaining a Complex Living System: Dynamics, Multi-Scaling and Emergence,” Journal of Royal Society Interface 4: 175-182.
Publisher – Google Scholar
Colijn, C., Fowler, A. C. & Mackey, M. C. (2006). “High Frequency Spikes in Long Period Blood Cell Oscillations,”Journal of Mathematical Biology 53: 499-519.
Publisher – Google Scholar
Colijn, C. & Mackey, M. C. (2005). “A Mathematical Model of Hematopoiesis: II. Cyclical Neutropenia,” Journal of Theoretical Biology 237: 133-146.
Publisher – Google Scholar
Colijn, C. & Mackey, M. C. (2005). “A Mathematical Model of Hematopoiesis–I. Periodic Chronic Myelogenous Leukemia,” Journal ofTheoretical Biology 237:117-32.
Publisher – Google Scholar