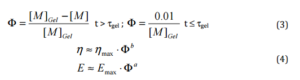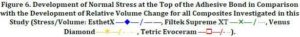Introduction
For nowadays tooth restorations, a great variety of materials can readily be used. Amongst them, light curable composites are suitable for many different applications and are not limited to cavity filling. Dental composites fulfill high aesthetic demands and their properties have been improved significantly over the last few decades. Their assessment however should include their resistance to mechanical loading and their mechanical burden on the necessary adhesive material by induced shrinkage stress. Loading stresses arise also in the adhesive material due to heterogeneous compliance. To achieve a suitable restoration the mechanical properties of the replaced tooth material should be considered. Human teeth have a compliant dentin core. Barak et al (2009) mentioned that this core supports an abrasion resistant tough outer enamel layer connected with a soft zone that hinders the delamination from the enamel. A mechanically suitable restorative material withstands stress and strain deformation without overloading its adhesive bonding and the surrounding natural tooth structure. There are typically two possibilities to meet the challenges of durable replacement and adequate load transfer to the root, as long as practitioners are still limited to using artificial homogeneous restoration material. One choice would be to use a material with superior strength and adapt the tooth basis to a shape that limits adhesive bonding to compressive situations. But the minimal invasive procedures require mimicked tooth material for high C-factors, otherwise the mechanical mismatch of compliance will induce excessive loading of the weakest component — the bonding. Braga et al (2013) mentioned a higher C-factor will lead to higher stress. The setting of the material is another important aspect that influences the quality of the bonding. Despite intensive research, light cured composites still undergo polymerization shrinkage that induces internal stresses in a cavity as was mentioned by Watts et al. (2003), Lu et al. (2004) and Stansbury et al. (2005). The shrinkage is of a hydrostatic nature, but since the ratio of free surface to bonded surface is small the deviatoric material can only compensate shrinkage with the similar ratio. Therefore stresses built up, that result from hindered shrinkage and viscoelastic shear flow. The goal of material development is to sustain a material with high strength that does not overload the critical bond to the tooth. To prevent failure after restoration suitable model experiments have to be conducted. In fact this is a challenging task, since material strength and polymerization strength are usually optimized separately. Following this need we developed a testing approach for dental composites which includes a coupled experimental and numerical method. Resulting with a successful model we are able to numerical estimate loading and shrinking stress of arbitrary cavity geometries, preparation techniques and mastication assumptions. The resulting stress distribution is very inhomogeneous, dependent on the cavity geometry and on its position. The character of the stress transfer to the adhesive bond changes continuously from normal dominant to shear dominant fractions. The level of adhesive strength, set by a preparation in optimal laboratory conditions, indicates that highest local shrinkage stress requirements could be met. In a research study Sano et al. (1994) pointed out that local stress can easily exceed mean strength due to small defects in the bonding zone or if the full adhesive strength was simply not achieved due to a contaminated bonding area as was mentioned by Sunico et al. (2002). The mechanical strength necessary to withstand internal stress and chewing load of composites is typically measured by three-point bending tests, a suitable method with easily achievable specimen geometry. Under bending load, the strength of a brittle material is determined by fracture at a certain tensile stress. Since chewing also induces excessive compressive stresses, other mechanical testing methods should be taken into account for restorations in load bearing areas. Relying on uniaxial composite strength tests does not take the complexity of the inner heterogeneous stress and strain behavior into account. The composite viscoelastic and shrinkage behavior results from heterogeneous material deformation tangential and normal to the filler surface causing loading of the adhesive bond of the filler and polymer. In conclusion the multiaxial strength of the composite should be incorporated for a comprehensive study by a variety of testing geometries. De Groot et al. (1987) and others already introduced the phenomenological Drucker Prager multiaxial failure criteria that was originally used for concrete but can similarly be applied on precursor ceramics after hot and dry pressing. In contrast to a principal stress criteria, as should be used for brittle homogeneous material in absence of shear strain, the Drucker Prager criteria is based on a critical von Mises to hydrostatic stress ratio. Maybe the simplest way to describe the effect inshort, the von Mises stress should be used for tests on a pure viscoelastic polymer material itself and the superposition with the hydrostatic stress includes the effect of adhesively incorporated particles as was investigated by Lohbauer et al. (2006). The aim of this paper is to present experimental und numerical methods to compare a simplified but comprehensive mechanical short term behavior of four dental composites. This behavior includes multiaxial mechanical resistance to load and strain as well as mechanical loading of the adhesive bond during setting. The loading of the adhesive bond has to be numerically calculated and the necessity of a simulation with or without material flow was investigated. Since there is no standardized way for curing a composite in a cavity, first simulations on the impact of layering technique or slanting of edges were tested.
Materials and Methods
Materials
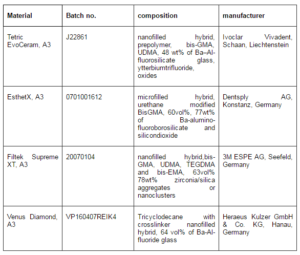
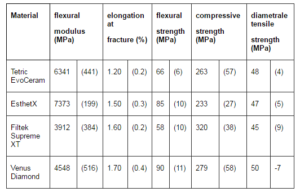
The materials used in this study are commercially available, light – activated resin composites (see table 1). For photo-initiation, a Translux Energy (Heraeus Kulzer GmbH & Co. KG, Hanau, Germany) halogen light source was employed.
Table 1: Composite Resins Used in this Study
Experimental Setup of Strength Measurements
For each test 10 specimens were incrementally cured and then treated with 300-grit sand paper on the basis of EN ISO 4049. The experimental procedure was as follows: Three-point flexural strength was measured according to EN ISO 4049 at loading speed of 0.75 mm/min. The flexural modulus was estimated by linear regression at strains from 0.01 to 0.02. The compressive strength was determined with cylinder shaped specimen Ø = 4mm, l = 8mm at a (facial) loading rate of 29 N/min and the diametral tensile strength was measured with cylinder shaped specimen Ø = 6mm, d = 3mm at a loading speed of 5300 N/min until fracture. The loading speed at chewing is debatable but much higher than for the standardized flexural experiment.
Experimental Procedure for Parameter Estimation of the Curing Model
The experimental setup was designed to fit in a servo-hydraulic testing machine. For each composite 5 disc shaped specimens (height 2.5 mm, diameter 5 mm) were prepared and loaded longitudinally to the cylinder axis in compression. A strain-optimized load-step-recovery series was chosen with increasing step length to produce low but sufficient strain steps of ~0.5% in order to obtain a linear material behavior as well as a good signal-to-noise ratio. For these conditions, the loads had to be increased in magnitude and in duration. By this strategy the additive strain behavior of the composite can be divided during a load step: shrinkage, elastic, viscous and viscoelastic behavior (i.e. a behavior which can be described by a Kelvin-Voigt model) due to their phenomenology. A detailed description was given by Koplin et al. (2009).
Curing Model
The kinetic behavior of curing dental composites has been described by Koplin et al. (2008) using a macroscopic polymerization model, based on the mixed termination model that was mentioned in the review of Andrzejewska (2001) (1). During polymerization the evolution of the »participating monomer« concentration [M(t)] passing the concentration level [M] t at the end of photo-initiation and the evolution of »radical-activated centers« is determined by the initiation, propagation and termination steps of the reaction. As a simplification a »participating monomer« concentration level of zero is reached, when the material is vitrified and the left monomer immobilized or trapped. The coefficients kp(propagation) and ktb (bimolecular termination) are diffusion-controlled. These coefficients change during the polymerization process partially due to the change in dominance occurring between different diffusion processes. The coefficient ktm is a more structure dependent coefficient (monomolecular termination) and was fixed to a probable value. The resultant volume shrinkage Dv was assumed to be linearly connected to the concentration of already converted participating monomer reaching the final value Dv (2).

This kinetic model includes descriptions of the initiation phase as well as the dark phase but does not include the auto-acceleration. The three-dimensional behavior of the composite is simulated using the four-parameter viscoelastic model with a volumetric shrinkage component (figure 1).
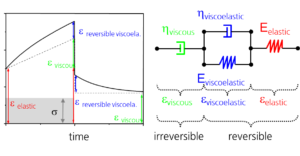
Figure 1. The Constitutive Four Parameter Viscoelastic Model is Symbolically Illustrated as a 1D Additive Strain Model Including a Volumetric Shrinkage Component
This model predicts the evolution of various material parameters (i.e. increase of stiffness and viscosity) during the polymerization reaction, based on the progress of the polymerization reaction. As a result, an integral description of the mechanical behavior during the curing process is obtained. As a simplification measure, the mathematical dependence of the material properties on the degree of crosslinking (3) was expressed as exponent a,b,c for each constitutive element of the viscoelastic model (4) f after the gel-point tgel.
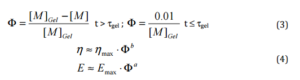
Cavity Simulations
The finite-element based simulations were conducted on ABAQUS software by Simulia using an implicit solver and user defined material behavior. Knowing that an inclusion of full complexity of a tooth restoration would encrypt fundamental results of stress and strain distributions by trying to parameterise tooth behavior and true geometric situations, it was simplified. Instead of that the strategy was chosen to simplify wherever possible and detail whenever necessary. Following this strategy, two different cylindrical shapes (fig. 2; A: r=5mm, h= 10mm; B: r=4mm, h= 4mm) with an averaged tooth-like material behavior for enamel (E=75 GPa and n=0.3), dentin (E=16 GPa and n=0.3), and a softer transition zone (E=6 GPa and n=0.3) were chosen. Cavity B was chosen to result in comparable curing conditions as were chosen by the authors before, but at the same time providing a more relevant simplification for detailed simulations by using cavity A. Since the material behavior of the tooth and composite was modeled with linear stress dependence, the entire size is scalable leaving stress and strains unaltered. The results can therefore be used on small cavities in small teeth as well as bigger cavities in bigger teeth, as long as aspect ratios are similar. But in fact the tooth behavior is highly orthotropic, individually and spatially distributed, as well as size-dependent as was mentioned by Ang et al. (2010). The simplifications were done on literature data for validated finite-element models by Barak et al. (2009). The outer geometry was set containing a cavity with nearly cylindrical geometry (A: r=2.1mm, h=1.5mm or B: r=1.3mm, h=1.75mm) which then was filled by curing the composite (figure 2).
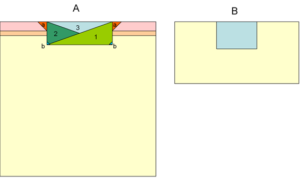
Figure 2. Longitudinal Section of Cylindrical Cavity Geometries Used in this Study
Results
Strength
Table 2: Strength Values of the Composites Used in this Study
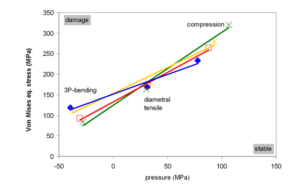
All results are summarized in table 2. The material does not only fail under pure uniaxial tensile loading but also under uniaxial compressive and triaxial loading, following the phenomenological theory of Drucker Prager. The different testing geometries induce different ratios of von Mises equivalent stress to hydrostatic stress. The Mises equivalent stress is useful to describe plastic and strain driven failure that is equivalent to uniaxial loading and is therefore useful for most polymers. By increasing the hydrostatic stress, higher von Mises stress can be sustained. The plotted lines (see fig. 2) split stress states to their consequences if leading to damage or not. The results show in bending a high critical von Mises stress for EsthetX and Venus Diamond. In bending von Mises stress as well as hydrostatic stress have damaging effects leading to lowest strength values for all materials. Venus Diamond has a higher mean strength according to the fitted Drucker-Prager criteria between uniaxial tensile and compressive loading (figure 3).

Parameter of a Curing Model
The moduli relating strain and stress for an isotropic material can be expressed by the moduli obtained through 1D loading tests and the Poisson constants for all four of the constitutive elements of the viscoelastic model (see table 3). They increase to a maximum value for the experiment after 300s. E0, h0 determine the elastic behavior, h2, n2 determine the viscous behavior and E1, h1, n1 determine a reversible behavior that is known as Kelvin-Voigt behavior. The aesthetic hybrid EsthetX, being the only microfilled composite, having no nanosized filler fraction and classical polymeric matrix shows the highest volume shrinkage. It also has the highest viscosity. This clearly indicates a different composition to achieve – for example a similar elastic modulus of the composite after curing. For Venus Diamond the highest elastic modulus and the lowest volume shrinkage were measured. A comparable low volume shrinkage was found for Tetric EvoCeram. A higher initial polymerization rate during the initiation phase can be found for EsthetX and Tetric EvoCeram by this resulting in a lower [M] t . The input of a single parameter on the internal stress development will be discussed later with the cavity simulations. A comparison of the overall viscoelastic moduli, by assuming additive strain components, gives a qualitative similar ranking of the observed three-point flexural moduli (see figure 4). The observed elastic moduli clearly differ, since the observation frequency for the final loading step is 1/40 s-1 and by this roughly 10 times slower than the inverse rate for the bending method.
Table 3: Parameter of the Curing Model for All Resins Used in this Study



Cavity Simulation
In order to simulate the build-up of internal stresses during the curing of a dental filling, two different cylinder shapes (fig. 2) with an averaged tooth-like material were chosen. Each contains a cavity with nearly cylindrical geometry which then was filled with a curing composite. The highest stress occurs for both cavities (fig. 5 based on fig.2 A) at the top of the adhesive bond at the restorative surface. There, the normal stress component is more than twice as high as the shear stress component.
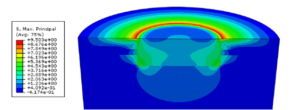
Figure 5. Resultant Maximal Principal Stress after 300s of Curing for Cavity a and Venus Diamond
Simulation of a Restoration during the Curing Process
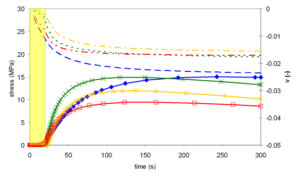
The normal stress (fig. 6) at the critical area at the top of the adhesive bond obtained by this restoration simulation is shown to be highest for the lowest filled composite EsthetX. But by comparing the tendency to build up lower shrinkage stress, Tetric EvoCeram is superior and Venus Diamond comes in the second place. A maximum of the stress is formed after ~2 minutes, except for EsthetX. The rate of the increasing stress is highest for Filtek Supreme XT.
Parameter Study
A variational study for the parameter of Venus Diamond was done by calculating the increase in one parameter by 10% and recording the change for the highest stress in % at the same position as above (see table 3).
Simulation of Different Cavity Aspects
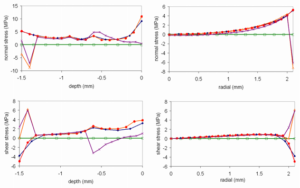
An easy and straightforward incremental layering approach was chosen (fig. 2 A) to simulate the resulting curing stress. The formerly identified localized region of highest stress at the top of the adhesive zone (fig. 5) was chosen to investigate this specific incremental layering effect. 200 seconds delay from the initiation of one increment to the other was chosen, and after a maximum value was reached the plot of the development of stress was truncated to simplify the resulting diagram (fig. 7).
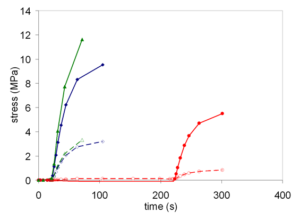

Whether a slanting technique leads to decreased stresses, was investigated by the finite element simulations for slanted and normal cavities (fig. 2 A, part a). The 45° slanted edge results in a dramatic decrease of the high localized stress (fig. 8) but leads to other effects. The chosen ordinate either corresponds to the depth starting from the surface of the cavity or the radial position at the bottom of the cavity. The typical stress vector on the adhesive zone basically points to a position slightly below the geometrical center of the cavity. By allowing an increase of material flow and a decrease of stress by slanting this edge (fig. 2 A, part a) high shear stress at the lower corner of the slanted edge is the logical consequence. The slanting of the edge at the bottom of the cavity that could also be called a rounding of the edge (fig. 2 A, part b) transforms the former high shear stress to higher normal stress. Concerning the internal stress an occurring benefit of this technique is unlikely. The resultant plots additionally verify that the 2D axisymmetric simulations give similar results as the 3D simulations.

Discussion
The approaches that can be found for the kinetic model of the curing differ from each other. Often the effect of auto-acceleration is included but the dark phase is not. An interesting review article has been given by Watts (2005). The first combining approach for a numerical kinetic model that includes initiation phase, auto-acceleration, temperature as well as spatial components seems to have been given by Matias et al. (2009) for photo-fabrication processes. A methodological approach that allows the necessary parameter estimation for this challenging model is still missing. Based on these findings the authors chose an approach estimating the development of mechanical parameter in correlation with the underlying monomeric conversion by its volumetric change rather than parameters determined at specific states. The practicability of this approach was recently affirmed by the explorative research on multiple correlations on material parameters by Li et al. (2009). The constitutive viscoelastic material model for curing dental composites can be simplified to a four-parameter model as was mentioned by Watts (1994), El-Hejazi et al. (1999), Vaidyanathan et al. (2001) and Vaidyanathan et al. (2002) consisting of three additive strain behavior that can be measured by sequential partial stress-relaxation experiments: elastic (E0, n0), viscous (h2, n2 ) and viscoelastic behavior (E1, h1, n1) (i.e. a behavior which can be described by a Kelvin-Voigt model).
The results for the mechanical strength reflect the complexity of the different compositional approaches for the four composites. A simple answer seems to be nonexistent for questions like: what is the material with the best mechanical properties or least stress transfer to the bonding. A benchmark does imply that the examination should be based on clearly defined variables. Problematic is for example that the mechanical strength results show an excellent flexural strength for EsthetX and low value for Filtek Supreme XT, but the results for the compressive strength are reversed. All four show a similar diametral tensile strength. By choosing the testing geometry, one should consider the scope of application that the composite is designed for. Therefore, the question that has to be answered is whether compressive, tensile or multiaxial loading is relevant. If a mean strength was calculated with respect to the Drucker Prager analysis than Venus Diamond would have the best mean mechanical properties. For an analysis of the tendency to build curing stress it is difficult to recognize a priori in which a combination of model parameters will result in a minimal shrinkage stress. The parameter study with respect to simulated values of Venus Diamond shows that single parameters like shrinkage, elastic modulus etc. are not sufficient in predicting the behavior since at least nine parameters show a strong influence on the resulting shrinkage stresses (parameter variation of 10% is followed by stress increase above 1 %; see results table 3). The parameter study was not extended to consider the interference of the parameters since all parameters could have a relevant influence on each other. Tetric EvoCeram has the lowest tendency to build up shrinkage stress and one can conclude that this is due to its low volume shrinkage, moderate elastic modulus and high proportion of monomer conversion during the initiation. An observed high conversion of monomer at the beginning leaves time for a relaxation of stress when conversion is slower in comparison to other materials. The resultant shrinkage stress, that has to be withstood by the adhesive bonding, is very inhomogeneous and varies strongly in its ratio of normal to shear components. Normal and shear strength components of an adhesive bonding depend strongly on the complex adhesive treatment and on the inhomogeneous tooth material. Material flow is driven by the hydrostatic shrinkage stress. At the top of the adhesive bond the hindered material flow to the center of the cavity induces high normal stress. By this it hinders partially the material flow from the free surface to the center inducing high shear stress as well. The relaxational flow and the presence of a free surface in the middle prevent the accumulation of higher stress. In consequence the lowest and the highest residual stresses occur at the surface. At the bottom of the cavity, the stress increases due to the hindered material flow. However, this increase is relatively small when compared to the higher stress found at the surface. The resultant mean adhesive stress is on a comparable level with the results of Yamamoto et al. (2009) ranging from 4.2 MPa to 7.0 MPa. Micro tensile bond strength may reach ~30 MPa for dentin or ~ 23 to 34 MPa for enamel as was found in the research study by Meerbeek (2011). By slanting the edge, the adhesive area is increased as well as material flow is allowed towards the center. In doing that the normal stress is drastically reduced but the high shear stress is accumulated at the newly generated edge. The positive effect of this type of slanting can only be judged by knowing the shear and normal strength of adhesives at the enamel and dentine. The slanting technique at the bottom of the cavity seems to have mostly negative effects with respect to solely shrinkage stress, since high localized normal stress is induced. The original sharp edge at this point does not lead to a high localized stress peak. This is due to the fact that the average normal to the fillet adhesive surface is not orthogonal to the stress vector. Following common knowledge that an increased ratio of free to bonded surface area increases material flow and therefore, decreases the shrinkage stress, incremental techniques are often applied for deeper cavities. The incremental layering technique seems to be a powerful method to prevent an overload of the adhesive bond at the geometrically disadvantageous positions. The technique leads to lower stress and disrupts the cylindrical symmetry resulting in a higher loaded side in the part of the last layer. In this special case the localized stress could be reduced to 50 % by layering, and certain aspects should be further on considered. Quite often cavity simulations are done neglecting the material flow of dental composites. It can clearly be seen, that a corrected effective volume shrinkage can mimic the adhesive stress to a certain degree quite well, but they lead to false conclusions for sharp geometrical features e.g. at the edge at the bottom of the cavity.
Conclusion
The multiaxial mechanical load on restored teeth should be thoroughly investigated and used in rating procedures for mechanical performance of composite restaurations. As a simple choice the Drucker Prager criteria is a feasible tool for including the critical multiaxial stress of these composites for failure assessment.
The magnitude of the shrinkage stress cannot be predicted by a single model parameter and flowability should be included in the simulation of the adhesive bond. The slanting technique can be useful for the prevention of highly localized normal stresses at the top of the bonding by allowing an increased shear relaxation at this position and increasing the bonding area to enamel. Slanting at the inner edge has no positive influence on internal stress. In a nutshell the FE-simulations prove to be a necessary choice to understand the complex interferences for the mechanical behavior and development of restorations under loading or during curing.
Acknowledgment
This work was partially funded by “Heraeus Kulzer GmbH, Division Dentistry”. The role of the funding source was the delivery of the material Venus Diamond, the assignment and funding of the comparative study for dental composites.
References
Andrzejewska, E. (2001). “Photopolymerization Kinetics of Multifunctional Monomers,” Progress in Polymer Science, 26, 605-665
Publisher – Google Scholar
Ang, S. F., Bortel, E. L., Swain, M. V., Klocke, A. & Schneider, G. A. (2010). “Size-Dependent Elastic/Inelastic Behavior of Enamel Over Millimeter and Nanometer Length Scales,” Biomaterials, 31(7), 1955-63
Publisher – Google Scholar
Barak, M. M., Geiger, S., Chattah, N. L. T., Shahar, R. & Weiner, S. (2009). “Enamel Dictates Whole Tooth Deformation: A Finite Element Model Study Validated by a Metrology Method,” Journal of Structural Biology, 168(3) 511-20
Publisher – Google Scholar
Braga, R. R., Koplin, C., Yamamoto, T., Tyler, K., Ferracane, J. L. & Swain, M. V. (2013). “Composite Polymerization Stress as a Function of Specimen Configuration Assessed by Crack Analysis and Finite Element Analysis,” Dental Materials, 29, 1026—1033
Publisher – Google Scholar
De Groot, R., Peters, M. C. R. B., De Haan, Y. M., Dop, G. J. & Plasschaert, A. J. M. (1987). “Failure Stress Criteria for Composite Resin,” Journal of Dental Research, 66(12), 1748-1752
Publisher – Google Scholar
El Hejazi, A. A. & Watts, D. C. (1999). “Creep and Viscoelastic Recovery of Cured and Secondary-Cured Composites and Resin-Modified Glass-Ionomers,” Dental Materials, 15,138-143
Publisher – Google Scholar
Koplin, C., Jaeger, R. & Hahn, P. (2008). “Kinetic Model for the Coupled Volumetric and Thermal Behavior of Dental Composites,” Dental Materials, 24, 1017—1024
Publisher – Google Scholar
Koplin, C., Jaeger, R. & Hahn, P. (2009). “A Material Model for Internal Stress of Dental Composites Caused by the Curing Process,” Dental Materials, 25(3), 331-338
Publisher – Google Scholar
Li, J., Li, H., Fok, A. S. L. & Watts, D. C. (2009). “Multiple Correlations of Material Parameters of Light-Cured Dental Composites,” Dental Materials, 25, 829-836
Publisher – Google Scholar
Lohbauer, U., Frankenberger, R., Krämer, N. & Petschelt, A. (2006). “Strength and Fatigue Performance versus Filler Fraction of Different Types of Direct Dental Restoratives,” Journal of Biomedical Material Research, Part B: Applied Biomaterials, 76B, 114-120
Publisher – Google Scholar
Lu, H., Stansbury, J. W., Dickens, S. H., Eichmiller, F. C. & Bowman, C. N. (2004). “Probing the Origins and Control of Shrinkage Stress in Dental Resin Composites. II. Novel Method of Simultaneous Measurement of Polymerization Shrinkage Stress and Conversion,” Journal of Biomedical Material Research Part B, Applied Biomatarials; 71, 206-213
Publisher – Google Scholar
Matias, J. M., Bartolo, P. J. & Pontes, A. V. (2009). “Modeling and Simulation of Photofabrication Processes Using Unsaturated Polyester Resins,” Journal of Applied Polymer Science, 114, 3673-3685
Publisher – Google Scholar
Meerbeek, B. V., Yoshiharaa, K., Yoshida, Y., Minec, A., Munck, J. D. & Landuyt, K. L. V. (2011). “State of the Art of Self-Etch Adhesives,” Dental Materials, 27(1), 17—28
Publisher – Google Scholar
Sano, H., Shono, T., Sonoda, H., Takatsu, T., Ciucchi, B., Carvalho, R. & Pashley, D. H. (1994). “Relationship between Surface Area for Adhesion and Tensile Bond Strength- Evaluation of a Micro-Tensile Bond Test,” Dental Materials, 10, 236-240
Publisher – Google Scholar
Stansbury, J. W.,Trujillo-Lemon, M., Lu, H., Ding, X., Lin, Y. & Ge, J. (2005). “Conversion-Dependent Shrinkage Stress and Strain in Dental Resins and Composites,” Dental Materials, 21, 56-67
Publisher – Google Scholar
Sunico, M. C., Shinkai, K., Medina, III V. O., Shirono, M., Tanaka, N. & Katoh, Y. (2002). “Effect of Surface Conditioning and Restorative Material on the Shear Bond Strength and Resin-Dentin Interface of a New One-Bottle Nanofilled Adhesive,” Dental Materials, 18, 535-542
Publisher – Google Scholar
Vaidyanathan, J. & Vaidyanathan, T. K. (2001). “Flexural Creep Deformation and Recovery in Dental Composites,”Journal of Dentistry, 29, 545-551
Publisher – Google Scholar
Vaidyanathan, T. K., Vaidyanathan, J. & Cherian, Z. (2002). “Extended Creep Behaviour of Dental Composite Using Time-Temperature Superposition Principle,” Dental Materials, 19(1), 46-53
Publisher – Google Scholar
Watts, D. C. (1994). “Elastic Moduli and Visco-Elastic Relaxation,” Journal of Dentistry, 22, 154-158
Publisher – Google Scholar
Watts, D. C. (2005). “Reaction Kinetics and Mechanics in Photo-Polymerized Networks,” Dental Materials, 21, 27-35
Publisher – Google Scholar
Watts, D. C., Marouf, A. S. & Al-Hindi, A. M. (2003). “Photo-Polymerization Shrinkage-Stress Kinetics in Resin-Composites: Methods Development,” Dental Materials, 19, 1-11
Publisher – Google Scholar
Yamamoto, T., Ferracane, J. L., Sakaguchi, R. L. & Swain, M. V. (2009). “Calculation of Contraction Stresses in Dental Composites by Analysis of Crack Propagation in the Matrix Surrounding a Cavity,” Dental Materials, 25, 543-550
Publisher – Google Scholar