Introduction
Mathematics appears to be a difficult subject that students were found to be disinterested and not motivated; consequently perceived it negatively. Numerous efforts including adopting innovative approaches and tools are constantly employed to help address the difficulties in mathematics learning. Various technology-based learning methods/tools such as videos learning (Esteban, Gonzalez, & Tejero, 2000), computers (delMas, Garfield, & Chance, 1999), computer algebra system Mathcad (Zand & Crowe, 2001), wiki-based website (Peterson, 2009) and World Wide Web (WWW) (Schwarz & Sutherland, 1997; West & Ogden, 1998) have been adopted to motivate and develop students’ interest and consequently enhance performance. Griffith (1998) maintains that technology helps students to develop conceptual understanding and problem-solving abilities.
Research evidence in favor handheld technology, such as graphing calculator (GC) as an effective teaching and learning tool to improve performance, specifically in mathematics, is growing. The integration of GCs evidently yields positive effects (Seth & Willis, 2004), which among others include, gains in students’ learning outcomes, particularly in the learning of functions (Vonder, 1992), better understanding of the concept of Mathematics, a more student-centered learning and higher order thinking (Simonsen & Dick, 1997).
Literature Review
Understanding and applications of concepts and principles to solve problems (Ding, Anis, & Suriani, 2003; Luitel, n.d.) are essential in Mathematics, in general, and Probability and Statistics, in particular. Problem solving, as Noraini (2003) explains, “encompasses both applying mathematics to the solution of problem arising from the environment, and puzzling over and reasoning about questions that have arisen within a mathematical context”. Therefore, without the understanding of mathematical concepts, the principles and the problems related to them, it would be rather difficult to utilize them in solving problems. According to Waits and Demana (1999), and Dossey, Mullis, Lindquist and Chambers (1988), most students view mathematics as a subject that involves numerous “tricks”, memorizing of rules to “compute or solve” problems, and tedious and boring work, especially “when they only remember the endless drill exercises – the “do it until it hurts” kind”. Hence, it is not surprising that students who only memorize tend to be uncertain of how and when to apply their knowledge in solving mathematical problems.
To most students, Probability is viewed as an abstract field, i.e. rather difficult to imagine the scenarios described in the problem statements. Honeycutt & Pierce (2007) confer that “compounding the problem is the abstract nature of probability and statistics.” Munisamy and Doraisamy (1998) state, the probabilistic reasoning appears to be a difficult skill to acquire among most of Malaysian students and hence it is not surprising that they tend to perceive learning Probability as difficult. Honeycutt and Pierce (2007) and Kissane (1997) maintain that, in most instances, they tend to merely “focus on the use of an algebra of probabilities, with little intuitive feeling for the content, which tend to result in mis-concepts and eventually to errors in calculations.” Castro (1998) and John (2004) concur that most mistakes in the calculations of probability are due to the failure in conceptual understanding. Students tend to have underlying difficulties with rational number concepts, which are used in calculating, reporting and interpreting probability (Behr, Leshm, Post, & Silver, 1983). This could also be due to students having difficulty in grasping the vocabulary of probability, which consequently results in it being too abstract for most students. Students tend to give it a cursory reading of context, and merely focus on the numbers and key words in the problem statements. In reviewing some of the research findings, Bergeson’s (2000) concludes that students have difficulties in solving the word problems in mathematics.
The problems in Probability involve the laws of Probability and contain many abstract expressions, complex terms, and nested relationships that student find it difficult to understand, visualize and master the concept (Stephen & Robert, 1997). In addition, the terminology in Probability differs from the terms used everyday. Most students have difficulties distinguishing them. Bennie’s (1998) reports on the “Likelihood Scale” activity that he had conducted. Students were asked to place on a likelihood scale for the event “15% of Astros are blue. You Choose a blue Astro from a full pack with your eyes closed”, students indicated that it was “likely” as it could occur, rather than indicating it with the term “very unlikely” as expected for this event to happen. This could be due to ‘the outcome approach”, which as Konold (1991) maintains, students think that they are being asked whether an event will happen, rather than “quantifying” how likely the event is, i.e. to express the chance that the event will happen numerically, or the “quantification” problem as stated by Honeycutt and Pierce (2007). They are unable to “see” or “visualize” the result of a single trial as one of many such trials in an experiment, but regard it in isolation. They may have taught that they are to predict the outcome on a single trial, and do not express it in terms of relative frequency of occurrence for an event (Madsen, 1995). Thus, it could be the language problem, as pointed by Konold (1991), i.e. this problem is related to the interpretation of the word ‘probable’ as ‘likely to occur’. Therefore, a large proportion of students tend to find probability, especially conditional probability, difficult (UMTC2003, 2003). Consequently, it is not surprising, Probability is perceived conversely by students.
This misperception and negative perception ought to be corrected. Gal and Ginsburg (1994) expound that a Probability and Statistics course should allow the demand for further statistics instruction as well as facilitate statistical thinking in order to learn more Probability and Statistics without fear or pessimism. Students should show appreciation towards Probability and Statistics, think statistically or probabilistically, know when to apply and how knowledge of Probability and Statistics applies and relate to their professions and daily life. They ought be more positive and not perceive mathematics as only “a fixed static body of knowledge”, rather view it as an activity that requires their active participation in order to identify, investigate, explore, and communicate ideas attached to mathematical situation (Moreno-Armella & Cinvestar, 1999). Students’ interest/motivation towards Statistics and Probability, self-concept/confidence in Statistics and Probability, willingness to think statistically in everyday situations and appreciate the relevancy of on Probability and Statistics to their lives ought to be enhanced.
In addressing the challenge of developing a more positive attitude towards Probability, researchers have been examining/adopting various tools, including graphing calculators. Studies have found that students place high value to mathematics when GC is incorporated in their learning. They reacted positively and favored the use of GC in learning Mathematics, and found that it was easy to be used (Ha, 2008; Hasan, Azizan, & Kassim, 2005; Mohd Ayub, Ahmad Tarmizi, Abu Bakar, & Mohd Yunus, 2008; Noraini, 2004; Seth & Willis, 2004; Waits & Demana, 1994). GC enables students to focus on mathematics concepts and brings real world data into the classroom, in which GC helps them in the “visualization” of mathematics concepts (Martinez-Cruz & Ratliff, 1998) that eventually enables them to grasp and understand mathematical concepts better (Nik Rafidah, Zarita, & Safian, 2008; Noraini, 2006; Ron, 2004). A broader and better understanding and appreciation of specific topics, such as calculus, linear algebra, differential equations, and statistics, respectively from students have been reported too (Rosihan & Kor, 2004; Zarita, Husna, & Suraiya, 2004). A “crunching machine”, GC hastens the computational process, enables more examples to be shown faster and from the easier questions to the more complicated ones, as well as enhances students’ mathematics understanding (Ong, 2004). Bouck (2009) highlights that feature of GC encourages students to attempt/solve more mathematics problems.
Regrettably, there is limited research which focuses on the effects of GCs at the higher learning institutions and in Probability, particularly in developing countries. Its adoption in Malaysian mathematics curriculum and classrooms (Muhd Khairiltitov, 2003) too is at its infant stage. Being a relatively new educational technology, which has yet to be adopted widely in Malaysia (Sundram, 2008), research on its incorporation in Mathematics classrooms in Malaysia is thus inevitably limited too.
This study researched on pre-university students’ perception of the incorporation of GC in Probability classrooms. The adoption of GCs aimed at reducing students’ anxieties in learning Probability. It also aimed at enhancing the quality of mathematics education so that students would not face the risks of being left behind or marginalized by their peer in developed countries.
Methodology
This study is an experimental research which involves the incorporation of GC in learning Probability, a new learning method that students have no prior experience. GC instructional worksheets, which were prepared as modular lessons, were used during the intervention period.
A group of 32 students (24 males and 8 females) at a private university in Malaysia, who were in the foundation program, were involved in this study for one trimester of 14 contact weeks. They comprised a multiracial composition of Malay, Chinese Indian, and a small number of international students, ranging from 17 to 21 years old.
In order to measure the students’ perception of using GC in Probability classroom, a questionnaire, i.e. “Questionnaires on Students’ Perception on the use of Graphing Calculator in the learning and teaching Probability (QSP)” which consists of 22 likert-scale questions, ranged from ‘strongly disagree’, ‘disagree’, ‘neither agree nor disagree’, ‘agree’ to ‘strongly agree’, was employed. It is a paper-and-pencil questionnaire and is an adaptation of Noraini et al.’s (2003) questionnaire. Data collected from the QSP aimed at measuring six specific aspects: ‘Calculator usage’, ‘Quality of output from the calculator’, ‘Understanding of Probability concepts’, ‘Student’s confidence in problem solving’, ‘Communication’ and ‘Student’s attitude towards learning Probability’.
At the beginning of the trimester, four sessions of GC workshops were conducted to enable the students to explore the buttons on the GC in order to master its important key features. The GC intervention was conducted from week 4 to week 12. A general lesson would begin with the delivery of the theories, followed by GC aided instructional activities. GC instructional worksheets were distributed at each lesson. Students had the opportunities to interact and discuss with peers in carrying out the GC tasks. The instructor guided, facilitated and provided suggestions, if necessary, during the discussions. As students gained competency in mastering GCs and simultaneously in their comprehension of the lessons, the instructor relinquished the scaffolding process.
In week 13, the QSP was administered to the students. Students were informed of the confidentiality of their responses in the QSP.
Statistical analysis, i.e. descriptive statistics was applied to the QSP data.
Results
The results of students’ perceptions toward the incorporation of GC in learning Probability, with particular focus on the six aspects are shown in Table 1 and Figure 1. Similar to previous studies (Ha, 2008; Hasan, et al., 2005; Mohd Ayub, et al., 2008; Noraini, 2004; Seth & Willis, 2004; Waits & Demana, 1994), this study found that the students’ perception towards the use of GC in their learning of Probability is favorable. All aspects scored averages of 4.05 and above. The aspect of “Quality of output from the calculator” scored the highest mean of 4.64.
Table 1: Mean and Standard Deviation of the Six Aspects
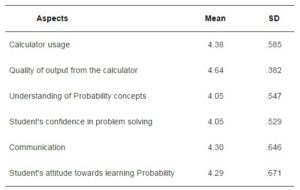
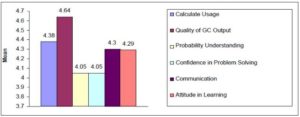
Fig 1: Students’ Perception on Six Aspects
To gain better insight into the nature and causes of the overall results on students’ perceptions towards the use of GC in learning Probability, the pattern of differences, of the overall mean and standard deviation for the six main aspects were further analyzed.
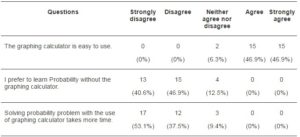
As shown in Table 2, it is obvious that students not only preferred learning probability with GC, they also found that with GCs, it was less time consuming to solve probability problems. The majority of the students, i.e. 93.8%, either agreed or strongly agreed that GCs are easy to use in learning Probability. Almost an equally large proportion of the students, i.e. 87% (40.6% strongly disagree and 46.9% and disagree) did not prefer to learn probability without the GC. 90.6% disagreed that solving probability problems with the use of GC is time consuming.
Table 2: Students’ Perception on the GC Usage
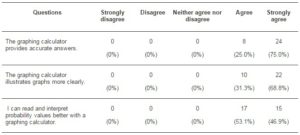
As seen in Table 3, all the students perceived that the output of the GCs are of quality, i.e. in terms of accuracy of answers, clear illustrations of graphs and ease of interpretation of value. However, they varied in their views in terms of levels of agreement. A higher proportion strongly agreed on the accuracy, i.e. 75%, followed by clear illustration, i.e. 68.8%. 46.9% strongly agreed that they could read and interpret the probability value clearly with GC.
Table 3: Students’ Perception on Quality of Output from GC
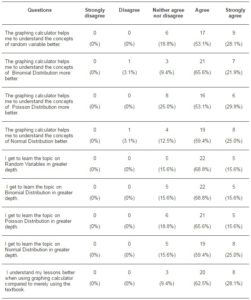
Further analysis on how GC helps in understanding the probability concepts was also made. As seen in Table 4, more than 80% of the students agreed that GCs helped them in understanding the concepts of the four topics better. No student disagreed that they did not get to learn the four topics in greater depth. Approximately 90% of them agreed that they understand their lessons better with the use of GC, compared to the use of textbooks. Only a small proportion of the students, i.e. 9.4% were unsure whether they understood their lessons better, when using GC compared to mere textbooks.
Table 4: Students’ Perception on How GC Helps to Understand Concepts
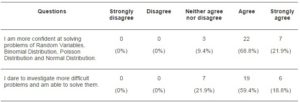
In terms of level of confidence in problem solving using GC, no student showed less confidence at solving problems of the four topics. As seen in Table 5, it is obviously the level of confidence in learning the topics had risen. Only 9.4% of the students have had indicated their views on whether GC has helped in increasing their confidence at solving the problems in the four topics taught. Conversely, 90.7% of students (68.8% agreed and 21.9% strongly agreed) concur that they were more confident to solve the problems of the four topics. In terms of whether the GC had increased students’ “daringness” to investigate more difficult problems, the results show that more than 70% of the students did, i.e. 59.4% agreed and 18.8% strongly agreed that they dared to investigate more difficult problems and be able to solve the problems.
Table 5: Students’ perception of their Level of Confidence
This study also found that the students’ communication abilities had improved. As presented in Table 6, 90.7% of the students have indicated that the GC had helped them in their discussions in the lecture/tutorial room. The GC had encouraged more than 80% of the students to interact with their instructor and friends. They had held many discussions on getting the solutions for the problems given on the instructional activities. They had also compared the answers from screen of the GC among themselves because it is a tool to explore more difficult problems and investigate many ‘what if’ situations.
Table 6: Students’ Perception on their Communication Abilities

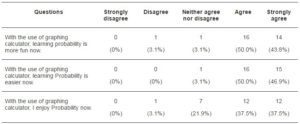
Lastly, almost all the students (94%) with exception of two students felt that learning Probability with GC is fun (Table 7) and in this fun learning environment, they were less anxious and felt that learning probability is much easier with the GC. 97% agreed that GCs creates an environment which enables them to learn Probability more easily. 75.0% enjoyed learning Probability now
Table 7: Students’ Attitude towards Learning Probability When Using GC
Discussion and Conclusion
The findings of this study clearly found favorable responds towards the use of GC as a tool that they were experiencing for the first time in learning Mathematics and specifically Probability. The majority of the students preferred learning Probability with the aid of GC. They found it to be a useful and user-friendly tool, which enabled them to perform several types of calculations, unlike other calculators. It enabled them to go beyond the seemingly impossible calculations. They did not find it to be complicated or difficult to use, rather easey to use and less time consuming. A large proportion of them expressed satisfaction with the quality of output produced from GC, which enhanced their understanding of the concepts, and consequently their level of confidence in solving probability problems. GC also provided a platform for active participation and interaction with instructor as well as peers. With increased understanding of concepts, levels of confidence and level of satisfaction, it is not surprising to observe a positive attitude towards learning Probability.
The outcomes of this study are consistent with the literature of GC. Students in this study too found GC to be a ‘crunching machine’ which hastens the process of solving complex mathematics problems. As Oldknow (1999) and (Shore, 1999) has pointed out, the ‘new found’ tool made the seemly ‘routine’ calculation ‘fun’, less time consuming, easier and faster to work on. As ‘visualizers’ and ‘graphic artists’, particularly in the performance of normal distribution, students were more focused and more observant. The graphing zoom-in feature enabled students to zoom-in on solutions of problems that were impossible to find using algebraic methods. The possibility of magnifying graphs at any given point and its multiple representations enabled students to visualize problems by monitoring the progress in problem solving, examining and exploring the mathematical patterns.
GC formed a ‘thinking tool’ in this study. It enabled students to develop conceptual understanding and problem-solving abilities in mathematics, particularly of the four topics addressed in this study, i.e. Random Variable, Binomial Distribution, Poisson Distribution and Normal Distribution. It gave room for the exploration of problem solving and in fact students ventured in more challenging problems confidently. With guidance from the instructor on the interpretation and analysis of the answers obtained from GC, the students had gained better and more meaningful understanding of concepts. Consistent with the literature, positive attitudes and motivation to learn Probability is also not surprising as most of the students found the learning with GC is fun, easy and enjoyable to work on.
The findings of this study are clearly consistent with the literature and hence add on to the body of knowledge and support for the incorporation of GCs in mathematics classrooms. With the increasing adoption of handheld technology, a better understanding and implementation of effective handheld technology will enhance the use and educational value of such educational technology. In general, this study clearly shows that the students significantly benefited as GC had played a vital role in improving their understanding and level of confidence in mathematics. It also proves to be a great learning tool in solving mathematic problems as well as in improving attitudes and communication abilities.
The positive perception of the students in this study is a clear indication that GC ought to be widely adopted by Malaysian mathematics educators. They ought to seize the vast potential of GCs that has much to offer in developing a positive attitude and motivation to learn Mathematics, which appears to be a difficult subject by most Malaysian students. This tool ought to be incorporated into the Malaysia educational system and more specifically, into the mathematics education. The Malaysian Ministry of Education ought to advocate, encourage and facilitate the use of GCs in institutions of learning.
Acknowledgement
We would like to thank StatWorks (M) Sdn Bhd for the GC loan, Noraini et al.’s (2003) for the adaptation of the instrument, and the Foundation Center for the permission of conducting this study to foundation students.
(adsbygoogle = window.adsbygoogle || []).push({});
References
Abdul Rahman, N. R. N., Zainuddin, Z. & Uda, S. (2008). “Using Graphic Calculators in Teaching and Learning Functions and Graphs at Matriculation Level,” Paper presented at the 3rd National Conference of Graphing Calculators.
Publisher – Google Scholar
Ali, R. M. & Kor, L. K. (2004). ‘Students’ Reactions to Learning Mathematics with Graphing Technology,’ Paper presented at the 2nd National Conference on Graphing Calculators.
Google Scholar
Behr, M., Leshm, R., Post, T. & Silver, E. (1983). ‘Rational Number Concepts,’ In Leshm.R. & Landau (Eds.), Acquisition of Mathematics. Concepts and Processes (pp. 264-344).
Google Scholar
Bennie, K. (1998). “The “Slippery” Concept of Probability: Reflections on Possible Teaching Approaches,” Paper presented at the 4th Annual Congress of the Association for Mathematics Education of South Africa (AMESA), Pieterseburg.
Publisher – Google Scholar
Bergeson, T. (2000). ‘Using Research to Shift from the ‘Yesterday’ Mind to the ‘Tomorrow’ Mind: Teaching and Learning Mathematics,’
Bouck, E. C. (2009). “Calculating the Value of Graphing Calculators for Seventh-Grade Students With and Without Disabilities,” Remedial and Special Education, 30(4), 207-215.
Publisher – Google Scholar
Castro, C. S. (1998). “Teaching Probability for a Conceptual Change,” Educational Studies in Mathematics, 35, 233-254.
Publisher – Google Scholar – British Library Direct
DelMas, R. C., Garfield, J. & Chance, B. L. (1999). “A Model of Classroom Research in Action: Developing Simulation Activities to Improve Students’ Statistical Reasoning,” Journal of Ststistics Education, 7(3).
Publisher – Google Scholar
Ding, H. E., Anis, S. & Suriani, M. (2003). ‘Action Research on Teaching and Learning Using Graphing Calculator,’ Paper presented at the 1st National Conference on Graphing Calculators, Malaysia.
Dossey, J. A., Mullis, I. V., Lindquist, M. M. & Chambers, D. L. (1988). ‘The Mathematics Report Card: Are We Measuring Up?,’ New York: Educational Testing Service.
Google Scholar
Embse, C. V. (1992). ‘Concept Development and Problem Solving Using Graphing Calculators in the Middle School,’ In J. T. Fey & C. R. Hirsch (Eds.), Calculators in Mathematics Education. Reston, Va: National Council of Teachers of Mathematics.
Google Scholar
Esteban, S., Gonzalez, M. P. & Tejero, L. (2000). “Videos as a Learning Support to Improve Mathematics Education. I. Advantages and Methodology,” Paper presented at the International Conference on “Mathematics for Living”, Jordan.
Publisher – Google Scholar
Gal, I. & Ginsburg, L. (1994). “The Role of Beliefs and Attitudes in Learning Statistics: Towards and Assessment Framework,” Journal of Statistics Education, 2(2).
Publisher – Google Scholar
Griffith, L. K. (1998). ‘Impact of Technology on Pedagogy,’ In E. D. Laughbaum (Ed.), Hand-Held Technology in Mathematics and Science Education: A Collection of papers (pp. 76-77). Columbus, OH: The Ohio State University.
Ha, T. Y. (2008). “Technology-Integrated Mathematics Eductaion (TIME): A Study of Interactions between Teachers and Students in Technology-Integrated Secondary Mathematics Classrooms,” University of Hawai’i.
Publisher – Google Scholar
Hasan, H. B., Azizan, M. B. & Kassim, S. B. (2005). “The Use of Graphic Calculators in Malaysian Secondary Schools: Students Perception and Teachers’ Constraints,” Paper presented at the 10th Asian Technology Conference in Mathematics.
Publisher – Google Scholar
Honeycutt, B. B. & Pierce, B. A. (2007). “Illustrating Probability in Genetics with Hands-On Learning: Making the Math Real,” The American Biology Teacher, 69(9), 554-561.
Publisher – Google Scholar – British Library Direct
Idris, N. (2004). “Exploration and Entertaining Mathematics: Why Graphic Calculator?,” Paper presented at the 2nd National Conference on Graphing Calculators.
Publisher – Google Scholar
Idris, N. (2006). “Exploring the Effect of TI-84 Plus on Achievement and Anxiety in Mathematics,” Eurasia Journal of Mathematics, Science and Technology Education, 2(3), 67-78.
Publisher
John, S. (2004). ‘Difficulties Encountered by College Students in Solving Probability Problems,’ Unpublished Master Project Paper/Research Report, Malaya University, Malaysia.
Kissane, B. (1997). “The Graphics Calculator and the Curriculum:The Case of Probability,” In N. Scott & H.Hollingsworth (Eds.), Mathematics: Creating The Future (pp. 397-404). Melbourne: Australian Association of Mathematics Teachers.
Publisher – Google Scholar
Konold, C. (1991). “Understanding Students’ Beliefs about Probability,” In E. V. Glaserfeld (Ed.), Radical Constructivism in Mathematics Education (pp. 139-156). Amsterdam, Kluwer.
Publisher – Google Scholar
Lancaster, R. (2004). “Twenty Years of Changes in Pedagogy and Content that Ultimately Gave Students a Richer and Deeper Understanding of Mathematics,” Paper presented at the Proceedings of the 2nd National Conference on Graphing Calculators.
Publisher
Luitel, B. C. (2003). (n.d.). ‘Developing and Probing Understanding,’ Retrieved November 6, from http://www.ses.curtin.edu.au~/understanding.htm
Madsen, R. W. (1995). “Secondary Students’ Concepts of Probability,” Teaching Statistics, 17, 90-93.
Publisher – Google Scholar
Martinez-Cruz, A. M. & Ratliff, M. I. (1998). “Beyond Modeling World Records with a Graphing Calculator: Assessing the Appropriateness of Models,” Mathematics and Computer Education, 143-153.
Publisher – Google Scholar
Mohd Ayub, A. F., Ahmad Tarmizi, R., Abu Bakar, K. & Mohd Yunus, A. S. (2008). “A Comparison of Malaysian Secondary Students Perceived Ease of Use and Usefulness of Dynamic Mathematical Software,” International Journal of Education and Information Technologies, 2(3), 194-201.
Publisher – Google Scholar
Moreno-Armella, L. & Cinvestar, M. S.-T. (1999). ‘The Use of Hand Calculators as Cognitive Tools in Mathematical Problem Solving,’ In E. D. Laughbaum (Ed.), Hand-Held Technology in Mathematics and Science Education: A Collection of papers (pp. 117-121). Columbus, OH: The Ohio State University.
Muhd Khairiltitov, Z. (2003). ‘Abstract: Penggunaan Kalkulator Grafik Di Sekolah-Sekolah Di Malaysia: Penerokaan dan Cabaran,’ Paper presented at the 1st National Conference on Graphing Calculators.
Munisamy, S. & Doraisamy, L. (1998). “Levels of Understanding of Probability Concepts among Secondary School Pupils,” International Journal of Mathematical Education in Science and Technology, 29(1).
Publisher – Google Scholar – British Library Direct
Noraini, I. (2003). ‘Communication in Mathematics: Usage of Graphing Calculator,’ Paper presented at the 1st National Conference on Graphing Calculators.
Noraini, I., Tay, B. L., Goh, L. S., Nilawati, M., Ding, H. E., Aziah, A. A., et al. (2003). ‘KaGUM Project 2001:A Graphing Calculator-Based Instruction and Its Impact on the Teaching and Learning of Mathematics,’
Ong, S. H. (2004). ‘Penggunaan Kalkulator Grafik Dalam Pengajaran Pengamiran Dan Graf Fungsi,’ Paper presented at the 2nd National Conference on Graphing Calculators.
Peterson, E. (2009). “Using Wiki to Enhance Cooperative Learning in a Real Analysis Course,” Primus, 19(1), 18-28.
Publisher – Google Scholar
Schwarz, C. J. & Sutherland, J. (1997). “An On-Line Workshop Uisng a Simple Capture-Recapture Experiment to Illustrate the Concepts of a Sampling Distribution,” Journal of Statistics Education, 5(1).
Publisher – Google Scholar
Seth, D. L. & Willis, L. (2004). ‘Graphic Calculator Explorations to Enhance Mathematics in Public High Schools,’ Paper presented at the 2nd National Conference on Graphing Calculators.
Shore, M. A. (1999). “The Effect of Graphing Calculators on College Students’ Ability to Solve Precedural and Conceptual Problems in Development Algebra,” West Virginia University, Morgantown,West Virginia.
Publisher
Simonsen, L. M. & Dick, T. P. (1997). “Teachers Perceptions of the impact of Graphing Calculators in the Mathematics Classroom,” Journal of Computer in Mathematics and Science Teaching, 16, 239-268.
Publisher – Google Scholar – British Library Direct
Sundram, M. (2008). “Designing Examination Questions by Incorporating the Use of Graphing Calculator,” Paper presented at the 3rd National Conference of Graphing Calculators.
Publisher – Google Scholar
Tomlinson, S. & Quinn, R. (1997). “Understanding Conditional Probability,” Teaching Statistics, 19(1).
Publisher – Google Scholar – British Library Direct
UMTC2003. (2003). ‘Brief 6: The Probability Problem. Paper presented at the Undergraduate Mathematics Teaching Conference,’ Birmingham, UK.
Waits, B. K. & Demana, F. (1994). “The Calculator and Computer Precalculus Project (C2PC): What Have We Learned in Ten Years?,” In E. D. Laughbaum (Ed.), Hand-Held Technology in Mathematics and Science Education: A Collection of Papers (pp. 12-32). Columbus, OH: The Ohio State University.
Publisher – Google Scholar
Waits, B. K. & Demana, F. (1999). ‘Calculators in Mathematics Teaching and Learning: Past, Present, and Future,’ In E. D. Laughbaum (Ed.), Hand-Held Technology in Mathematics and Science Education: A Collection of Papers (pp. 2-11). Columbus, OH: The Ohio State University.
West, R. W. & Ogden, R. T. (1998). “Interactive Demonstrations for Statistics Education on the World Wide Web,” Journal of Statistics Education, 6(3).
Publisher – Google Scholar
Zand, H. & Crowe, W. D. (2001, 15-19 December, 2001). “Distance Learners and a CAS-based Mathematics Course: Evaluation and Its Problems,” Paper presented at the the 6th ATCM Conference.
Publisher – Google Scholar
Zarita, Z., Husna, H. & Suraiya, K. (2004). ‘Ecological Modeling with the TI-92 Plus Graphics Calculator [Abstract],’ Paper presented at the 2nd National Conference on Graphing Calculators.










