Introduction

In education, the most three common academic timetabling problems are school timetable, university timetable and exam timetable. According to Bardadym (1996), university timetables are more complex compared to school timetables which have equal time slot and it is weekly repeated during a semester. Time slot for university timetable is not equal in length, some subjects are taught every week in weekdays, some of them are only taught during weekends, others are only taught in the first seven weeks of the semester, etc. At the end of each semester or trimester, most educational institution must prepare a set of examination schedules for their students. Usually, a timetable that has been used previously will be recycled and reused again. Some minor adjustments may need to be made and this can be done manually to ensure that the new exam timetable is acceptable.

According to Norberciak (2006), exam timetabling approach is divided into four classifications which are cluster or decomposition methods, sequential methods, constraint-based approaches and meta-heuristic methods. Three studies by Burke et al. (1994a); Burke and Newall (1999); Qu and Burke (2007), discussed the exam timetable using cluster or decomposition methods while Burke et al. (1998c) have proposed sequential methods for exam timetabling problem. Two studies by Deris et al. (2000); Kambi and Gilbert (1996), found that constraint-based approaches are suitable for exam timetabling problem.

Exam timetabling is the sub class of timetabling problem which its events take place in the university. Exam timetabling refers to the process of assigning exam entities to particular slots and rooms in the timetable. Students are required to be seated for one exam in the specific room during a specific time slot. Exam timetabling is one of NP-hard problems; therefore, creating an exam timetable is difficult to be done manually due to the complexity of the problem. These problems arise due to some reasons such as dual academic calendar, increasing student enrolments, limitations of resources,-… etc.

Constraints involved in this problem can be divided into two categories; hard constraints and soft constraints. Hard constrains are unacceptable problems which cannot occur at any percentage in order to consider the timetable as feasible. Normally, exam timetable will satisfy all hard constraints but the problem is how to measure it is a good timetable. Thus, soft constraints will be used as the measurement which will evaluate either the timetable is good and practical or not. According to Burke et al. (2004), soft constraints can be considered as preferences which will fulfil some of the user requirements to maximize the perfection of the timetable. In general, not every soft constraint can be satisfied.

Burke et al. (2004) also found that hard constraints and soft constraints are very subjective to define and it depends on the requirements of the universities. In some cases, constraint on room availability is unnecessary because that university has a large amount of rooms that can be used for exam. The constraints such as some exams must occur before other exams may not be relevant in some universities due to the fact that all exams have the same level and not a pre-requisite exam. According to Burke et al. (1996), for some exam timetabling problems, it is difficult to find a feasible solution at all. Whereas for other problems, there is a large number of feasible solutions and the focus of the problem solving is very much directed to the minimizations of soft constraint violations. 

The Study

Starting from Jun 2010 session, MMU has changed their academic calendar to dual calendar. Faculty and Centre for Diploma (CDP) used the same academic calendars while FOSEE used a different academic calendar. At the end of every trimester, Examination Unit (ERU) needs to prepare exam timetable for faculty, CDP and FOSEE.

The current practice for creating exam timetable in FOSEE, MMU only considers the hard constraints and ignores the soft constraints. For example, if the duration of the exam is seven days, the system will make sure that entire exams involved for current trimester will be spread out within that duration without utilizing the resources allocation, reducing student constraints or minimizing the invigilator constraints. With this practice, the invigilator normally needs to invigilate at least three exams and sometimes the exam will take place in a large room even though the number of students is rather small. Lecturers also face problems like they need to invigilate and mark the exam paper at the same time within the required time.

This study focuses on real exam data for foundation student in FOSEE, MMU, Malaysia. The exam timetabling problem for trimester 2, 2009/2010 session consists of planning 39 different subjects in seven days using eight venues with different capacity. This exam data involves five foundations with two intakes of students. In addition, each day there are only two slots available which are morning session and afternoon session. As mentioned before, the heuristic approaches will be applied to these data in order to reduce the exam duration and to guarantee that all exams are scheduled accordingly. Objective function will be used to figure out whether the proposed exam timetable is feasible or not compared to the previous exam timetable. A recent study by Cupic et al. (2009) found that the objective function of timetabling refers to the weighted penalty, which is assigned to soft constraints that are not satisfying.

Therefore, clustering heuristic will be applied in this study to split exams into groups and conflict between exams which is represented by conflict matrix. The objective function will be used to determine the solution quality for exam timetabling problem. While the graph colouring heuristic will be used to determine the number of exam slots for this problem.

Examination Timetabling Heuristics

Stating the constraints is very important as generally the hard constraints will find out the incompatible exam slot, and soft constraints will determine the solution quality of exam timetable.  As supported by Gogos et al. (2010), solution quality is normally interpreted as timetables which have sufficiently long periods between exams for each student. The main problem in exam timetabling is to assign exams to specific time slot which must satisfy the hard constraints with the objective of minimizing the soft constraints violation. 

There are several hard constraints that must be satisfied in this problem which are:

1. exam constraint – there is only one exam for each subject 
2. student conflict – a student cannot take two exams at the same time or slot 
3. seating restriction – the number of students seated for an exam cannot exceed the room capacity

And the soft constraint for this problem is:

1. a student should not have more than one exam per day

In exam timetabling problem, the objective functions will be used to measure how well the soft constraints are satisfied. This is important to determine the solution quality of the exam timetable as Penalty = 1 will be given if the soft constraints are unsatisfied.

After stating the constraints, decomposition of subject will take place. Foundation students in MMU will enrol different subjects based on their foundation and intake. These students then will be streamed into a specific group; therefore a large number of students can be dealt with as a single entity with a certain number of students. Students will be grouped based on their foundation and intake. Besides, the subjects will be divided into small groups called clusters which are based on the foundation and intake. Each cluster will be assigned with different colour representing their group. With this method, the problem size becomes smaller and it would be easier to determine the conflict matrix between the subjects based on the colouring approach.

These are the four steps that have been applied to decompose the entire subjects into cluster:

1. subjects will be divided into specific foundation 
2. subjects will be divided into specific intake 
3. assigning specific colour for each cluster 
4. sorting all the subjects in the cluster based on student enrolment 

One of the constraints in the decomposition of subject is that are some subjects that involved students from combination of foundation or intake or both. A special cluster will be created for a group with more than one colour which represents a subject with various characteristics.

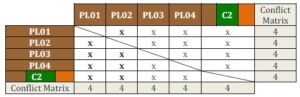
The next step is to determine the conflict matrix between the subjects. One of the most important aspects in exam timetabling problem is the conflict matrix which represents the hard constraint or a pair of clashing exams. The arrangement of the conflict matrix helps in determining the constraints that none of the students must attend more one exam at the same time or slot. Two subjects will clash if there is at least one student registered for both subject. Usually, the conflict matrix table is created to check whether two exams are clashing or not based on the student’s course registration in each trimester.

In Table 1 below, the ‘x’ represents those pairs of clashing exams based on their group colour.  For example, law students registered for five subjects are represented by PL01, PL02, PL03, PL04 and C2. All subjects have been assigned with exam code instead of using the subject name.  For example PL01; PL = foundation law, 0 = intake trimester 1 and 1 = subject.

Table 1: Conflict Matrix for Foundation in Law Clusters 

Once the conflict matrix is formed, graph colouring approach will be used to determine the exam selection. This method is used to find out the orders in which exams are selected. Through this approach, each exam is represented by different vertices where the edges between vertices represent the exam conflict. Colouring the graph is the process of allocating the different colour to each vertex so that two adjacent vertices will have different colours and each colour is equivalent to one period or slot in the exam timetable.

The objective of graph colouring is to find the minimum number of colours applied on the vertices of a graph so that none of vertices has the same colour. The chromatic number of a graph is the least number of colours it takes to colour its vertices so that adjacent vertices have different colours. Based on the literature, graph colouring is considered a NP-complete problem due to the fact that there is no efficient polynomial-time algorithm that can find the chromatic number for the graph.

Another way of checking the conflict matrix is to view it from a graph perspective. From a graph perspective, the total number of edges for the vertex equals to the conflict matrix for each subject in the matrix. The example refers to subject PL01. This subject belongs to cluster PL represented by brown colour. The total conflict matrix for this subject is four (refer Table 1); therefore, the total edges for the vertex in the graph colouring should be also four.

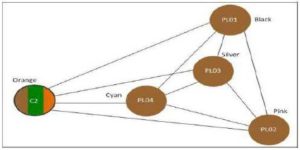
 Figure 1: Graph for PL01

Figure1 proved that conflict matrix in Table 1 can be used to find total number of edges in graph colouring. Vertex PL01 is coloured by brown because it represents cluster group colour while vertex C2 represents combination three colours due to the students who come from different foundation or intake register in this subject. Five vertexes represent that this law student (cluster PL) enrol in five subjects and these subjects cannot be scheduled at the same time slot due to the hard constraint condition.

Based on the literature, vertices with the same edge must be represented in different colours. These colours refer to graph colour and not a group colour. These processes will continuously select a vertex and assign it a new colour such that no two adjacent vertices have the same colour. A solution exists if the colour is equal to the number of vertexes in the cluster. Figure 1 has five vertexes with the same edge and the colour should be five colours which represent five different exam slots which are orange, cyan, silver, pink, and black.  However, the total conflict cannot be applied for special cluster due to combination of characteristic.

Result and Analysis

Decomposition subject will be done to reduce the problem size and determine the conflict matrix between the subjects. This method helps to define whether the subject can be a slot or be assigned in the same slot or not in the exam timetable.

For this study, all the 39 subjects will be grouped into eight different clusters which significantly have the similar characteristics based on their foundation and intake. Each of the clusters will have a group of subjects and will be represented by a unique group colour.

Once all subjects have been grouped in their designated clusters, they will be sorted according to the numbers of student enrolment. Then, each of these subjects will be assigned with a special code. For example PM01; is a subject for foundation management student which can interpret as PM = foundation management, 0 = intake trimester 1, 1 = subject and orange colour = group colour. Foundation in management, information technology and engineering has two intakes of students whereas foundation in law and life sciences only involve one intake.

Table 2: Cluster Group for Foundation with Two Intakes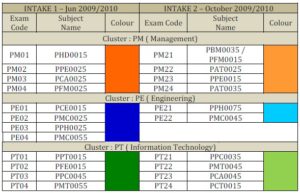

Table 3: Cluster Group for Foundation with One Intake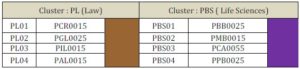

But after the decomposition of subjects, only 30 subjects are able to be grouped in these clusters since it is only suitable for the subject offered for one foundation and one intake but not for various foundation or intake. For example subject PEN0025 – English 1 is enrolled by student from foundation in management, information technology, engineering and life sciences for intake 1. In order to solve this problem, a special group called special cluster has been created for subject with combination foundation and intake. 

Subject for special cluster has one of the following characteristics:

1. enrolled by students from different foundations
2. enrolled by students from different intakes
3. enrolled by students from different foundations and different intakes

Conflict between subjects will be determined by using conflict matrix table. The maximum number of conflicts is 23 for subject C1. Subject C1 is a special cluster where it consists of the combination of students from four different groups.  While for normal cluster, the maximum number of conflicts is eight for subjects under PM and PE cluster. Based on conflict matrix, it shows that nine colours are used in the graph colouring to represent nine slots that should be used for this problem.

Table 4 below shows the entire nine colours and the subject for each colour with the student enrolment.

Table 4: Summary of Graph Colouring and Subject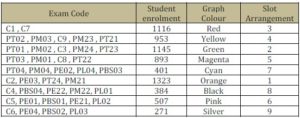

After all subjects have been grouped to the specific colour, they will be sorted according to the number of student enrolments. The exam with the highest number of student enrolments should be scheduled first.

Table 5: Slot Arrangement Based on largest Enrolment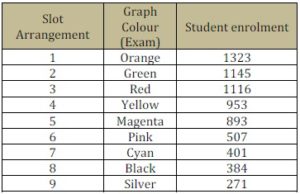

Period Selection Using Nine Slots

The constructive heuristic with the largest enrolment will generate initial solution by sequentially selecting an exam and assigning the exam to a feasible slot without violating any hard constraints. This algorithm begins with an exam with the highest enrolment and assigns it to the first available slot. If a slot is not available, the exam is put into the next available slot. A slot is feasible if it fulfils the soft constraint where a student should not have more than one exam per day. In this heuristic, the potential penalty of assigning exam to each period is calculated and the period with minimum penalty is selected.

Below are the steps involved in period selection using nine slots:

1. First, assign the orange exam slot to slot 1 (Monday morning) because it has the highest number of student enrolments. 
2. Then, the green exam slot should be assigned to slot 2 but it will violate the soft constraint, therefore, it should be moved and assigned to Slot 3 (Tuesday morning). 
3. The red exam slot should be assigned to slot 4 but it will violate the soft constraint too, therefore, it should be moved and assigned to Slot 5 (Wednesday morning).
4. Next, the yellow exam slot has to be assigned to slot 6 but it will violate the soft constraint, therefore, it should be moved and assigned to Slot 7 (Thursday morning).
5. The magenta exam slot should be assigned to slot 8 but it will violate the soft constraint, therefore, it should be moved and assigned to Slot 9 (Friday morning).
6. The pink exam slot cannot be assigned to slot 2, 4, 6 and 8 due to the soft constraint.  At this stage, penalty of assigning exam to each slot is calculated and the period with minimum penalty is selected.  Therefore penalty for slot 2 = 4, slot 4 = 4, slot 6 = 5 and slot 8 = 4.  Pink exam slot will be assigned to slot 2 since it is the first slot to consist with minimum penalty. 
7. Then, the cyan exam slot cannot be assigned to slot 4, 6 and 8 due to the soft constraint. Therefore penalty for slot 4 = 3, slot 6 = 4 and slot 8 = 3.  Cyan exam slot will assigned to slot 4 since it is the first slot to consist with minimum penalty. 
8. The black exam slot cannot be assigned to slot 6 and 8 due to the soft constraint. Therefore penalty for slot 6 = 6 and slot 8 = 5.  The black exam slot will be assigned to slot 8 since it is the first slot to consist with minimum penalty. 
9. Lastly, the silver exam slot will be assigned to slot 6 with penalty = 4

Table 6: Exam Timetable Using Nine Slots

Through this method, only 16 out of 39 subjects will violate the soft constraint. It also reduced the number of slots compared to the original exam timetable for trimester 2, 2009-2010 which is 12 slots. Even though this method is not an optimization option, but with this feasible solution it will help the management to ensure that all resources such as room and invigilator are well utilized with minimum number of exam slots. These methods give more advantages to the academicians compare to the students due to the decreasing number of exam slots from 12 slots to nine slots only.

Conclusions

This study has proved that through clustering and graph colouring heuristic, the duration of the final exam in FOSEE, MMU can be minimized. The development of exam timetable will be more systematic, effective and efficient. 

The use of clustering heuristic is very important as it decomposes the entire subjects based on their characteristic such as foundation and intake.  While the filtering technique uses conflict matrix table to recheck the clashing of subjects based on cluster colouring. Besides, the graph colouring heuristic is useful to determine the total exam slot needed without any clashing even though this approach is suitable for the problem that focuses on hard constraint.

This study only presents methods or approaches that can be applied for exam timetable without any automated or computerized system. It will be a good idea to include it as an automated system using specific tools and languages as the outputs are more consistent and the experiment can be performed to any problem size.

References

Bardadym, V. A. (1996). “Computer-Aided School and University Timetabling: The New Wave,” In E. K. Burke, & P. Ross, Practice and Theory of Automated Timetabling, 22-45.
Publisher – Google Scholar – British Library Direct

Burke, E. K. & Newall, J. P. (1999). “A Multi-stage Evolutionary Algorithm for the Timetable Problem,” IEEE Transactions on Evolutionary Computation, 63–74.
Publisher – Google Scholar – British Library Direct

Burke, E. K., Eckersley, A. J., McCollum, B., Petrovic, S. & Qu, R. (2004). “Analysing Similarity in Examination Timetabling,” Proceedings of the 5th International Conference on the Practice and Theory of Automated Timetabling, Pittsburgh, USA, 89-106.
Publisher 

Burke, E. K., Elliman, D. G., Ford, P. H. & Weare, R. F. (1996). “Examination Timetabling in British Universities: A survey,” In E. K. Burke, & P. Ross, Practice and Theory of Automated Timetabling, 79-90.
Publisher – Google Scholar – British Library Direct

Burke, E. K., Elliman, D. G. & Weare, R. (1994a). “A University Timetabling System based on Graph Colouring and Constraint Manipulation,” Journal of Research on Computing in Education, 1-18.
Publisher – Google Scholar – British Library Direct

Burke, E. K., Mccollum, B., Meisels, A., Petrovic, S. & Qu, R. (2007). “A Graph-Based Hyper-Heuristic for Educational Timetabling Problems,” European Journal of Operational Research, 176, 177-192.
Publisher – Google Scholar 

Burke, E. K., Newall, J. P. & Weare, R. F. (1998c). “A Simple Heuristically Guided Search for the Timetable Problem,” International ICSC Symposium on Engineering of Intelligent Systems (EIS98), 574–579.
Publisher – Google Scholar 

Cowling, P. I., Ahmadi, S., Cheng, P. C. & Barone, R. (2002). ”Combining Human and Machine Intelligence to Produce Effective Examination Timetables,” The 4th Asia-Pacific Conference on Simulated Evolution and Learning (SEAL 2002), Singapore, 662-666.
Publisher – Google Scholar 

Cupic, M., Golub, M. & Jakobovic, D. (2009). “Exam Timetabling Using Genetic Algorithm,” Proceedings of the 31st International Conference on Information Technology Interfaces (ITI 2009), Croatia, 357-362.
Publisher – Google Scholar 

Deris, S., Omatu, S. & Ohta, H. (2000). “Timetable Planning using the Constraint-based Reasoning,” Computers & Operations Research, 27, 819-840.
Publisher – Google Scholar – British Library Direct

Eley, M. (2007). “Ant Algorithms for the Exam Timetabling Problem,” Practice and Theory of Automated Timetabling VI: Selected Papers from the 6th International Conference, 364– 382.
Publisher – Google Scholar – British Library Direct

Gogos, C., Alefragis, P. & Housos, E. (2010), “An Improved Multi-staged Algorithmic Process for The Solution of The Examination Timetabling Problem,” Annals of Operations Research.
Publisher – Google Scholar 

Kambi, M. & Gilbert, D. (1996). “Timetabling in Constraint Logic Programming,” Proceedings of INAP-96: Symposium and Exhibition on Industrial Applications of Prolog, Tokyo.
Publisher – Google Scholar 

Malkawi, M., Hassan, M. A.- H. & Hassan, O. A.- H. (2008). “A New Exam Scheduling Algorithm Using Graph Coloring,” The International Arab Journal of Information Technology, 80-87.
Publisher – Google Scholar 

Norberciak, M. (2006). “Universal Method for Timetable Construction Based on Evolutionary Approach,” World Academy of Science, Engineering and Technology, 91-96.
Publisher – Google Scholar

Qu, R. & Burke, E. K. (2007). “Adaptive Decomposition and Construction for Examination Timetabling Problems,” Multidisciplinary International Scheduling: Theory and Applications (MISTA’07), 418-425.
Publisher – Google Scholar 

Rahman, S. A., Bargiela, A., Burke, E. K., Ozcan, E. & McCollum, B. (2009). “Construction of Examination Timetables Based on Ordering Heuristics,” 24th International Symposium on Computer and Information Sciences, 680-685.
Publisher – Google Scholar 

Schaerf, A. (1999). “A Survey of Automated Timetabling,” Artificial Intelligence Review, 87-127.
Publisher – Google Scholar – British Library Direct

Sheibani, K. (2002). “An Evolutionary Approach for the Examination Timetabling Problems,” In E. Burke, & P. D. Causmaecker, Practice and Theory of Automated Timetabling: 4th International Conference, Belgium, 387-396.
Publisher – Google Scholar 

White, G. M. & Xie, B. S. (2001). “Examination Timetables and Tabu Search with Longer-term Memory,” Practice and Theory of Automated Timetabling III: Selected Papers from the 3rd International Conference, 85–103.
Publisher – Google Scholar – British Library Direct

Wren, A. (1996). “Scheduling, Timetabling and Rostering — A Special Relationship?,” In E. K. Burke, & P. Ross, Practice and Theory of Automated Timetabling, 46-75.
Publisher – Google Scholar – British Library Direct