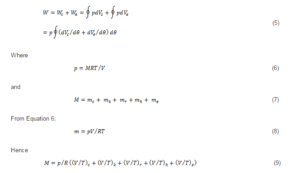Challenges in Developing a Domestic Solar Thermal Electricity System Using a Stirling Engine

Introduction

Nowadays the use of renewable energy sources is rapidly increasing in its importance. This is mainly due to the fact that certain countries are now bound by legislations to reduce carbon emissions and reduce their dependency on fossil fuels. For example member states of the European Union are bound by EU directives which specify the percentage amount of the final energy consumption that should be produced from renewable sources by the end of 2020. Small countries such as Malta, have limited open area at ground level that can accommodate large grid connected concentrated solar power or large photovoltaic systems. However, considerable space exists on domestic and industrial roof tops. In Malta most buildings have flat roof tops making them quite versatile for installation of these renewable energy systems.  The current trend is to cover these roof top areas with photovoltaic (PV) panels. This is due to the photovoltaic panels’ reliability and reasonable efficiency. A PV system consists of a number of PV modules where each module consists of a number of solar cells, when incident solar radiation shines on a solar cell, the photon is absorbed and electron-hole pairs are generated. This will generate a flow of direct current that is fed to an inverter, where this is converted into an alternating current and consequently consumed or fed into the grid. The three main types of PV module technologies amongst the various available are monocrystalline silicon, polycrystalline silicon and thin film. The main differences between the performance is that the efficiency of the monocrystalline and the polycrystalline decreases as the temperature of the panel increases; while the efficiency of thin film remains fairly stable. On the other hand the efficiency of monocrystalline and the polycrystalline is approximately 2.5 times higher than that of thin film, making them the most suitable technologies when the area available is limited. The output of a PV system decreases with the age of the system. From the technologies available today, the one should expect the output to reduce to 90% after 10 years of operation and to 80% after 25 years of operation. PV systems are still limited in their efficiency and although their price has significantly descreased it is interesting to test the undiscovered potential of micro-scale concentrated solar power heat engines. Such a heat engine system may result in a better solution in terms of cost and efficiency.

Solar-powered Stirling engines can potentially be alternative candidates for micro-scale solar systems for domestic use. Currently, Stirling engines are mainly powered by concentrating solar energy at the focal point of parabolic dishes. For these systems, the minimum size of the dish is about 3.75m in diameter. This size of dish is quite prohibitive to be installed on a domestic rooftop. Problems that can be encountered include wind loading, aesthetics and acquiring local planning permits for such installations. This paper describes the proposed development of a system utilising parabolic troughs as energy collectors. A heat transfer fluid passes through the receivers which are located in the troughs’ focal line.  The energy absorbed by the heat transfer fluid is then used as a heat source for the Stirling engine. There are a number of advantages for such a system; one of these advantages is that the size of parabolic troughs is quite similar to that of photovoltaic panels. Therefore, they are less subjected to wind loading and are aesthetically more pleasing. Another advantage of such systems is the potential for energy storage to cover periods of indirect sunlight. The major challenge of the proposed micro scale concentrated solar power system is the relatively low temperature (250-350°C) that can currently be reached by small aperture parabolic troughs. Thus, a Stirling engine which gives a reasonable power output and efficiency at this temperature range has to be developed. Nearly all Stirling engines available on the market operate at a temperature higher than 650°C (D.Thimsen, 2002). Moreover, in order to be competitive, the efficiency and cost of the complete system has to be at least in the same level as the photovoltaic panels.

A Stirling engine is a heat engine that subjects the working fluid to a closed loop cycle. An external heat source is used to supply heat to the engine. This results in a relatively silent engine in comparison with IC engines since no explosive combustion is occurring. Another advantage of the Stirling engine is that less ‘toxic’ exhaust is emitted by the engine. Furthermore, the Stirling engine requires low maintenance and creates minimal vibrations. This makes the engine a good candidate for installing on the roof tops. Studies were conducted to analyse what Stirling engines are available on the market and whether they operate at the temperature of 250 to 350°C reached by small aperture parabolic solar troughs. In these studies the authors were analysing engines that deliver 3kW of shaft power or less. From this investigation it was concluded that the majority of the existing engines are prototypes and few are ‘commercially’ available. Furthermore, the majority of the engines surveyed operate at a temperature above 500°C. The engines surveyed were developed by: Genoa Stirling, which has a variety of 3 engines ranging from 350W, 1kW and 3kW and working temperature of 750°C (Genoastirling, 2011); Sun Power, who offer a 1kW free piston engine (SunPower, 2012); Whispergen, offer a 1 kW kinematic Stirling engine which is used in micro combined heat and power unit (Whispergen, 2012); Infinia who offer two engines (1kW and a 3kW) both free piston  (Infinia, 2012) and Microgen  who developed a 1kW free piston engine. (Microgen, 2012), Only one engine was found to operate at temperature below 300°C. This latter engine is still in the testing phase and was  being developed by Cool Energy (Coolenergy, 2012). From the market survey it was concluded that it is clear that a Stirling engine operating at a low/medium temperature range is not readily available, and this leaves scope for development of such an engine.

Thermodynamics of the Stirling Engine

The thermodynamic cycle of a Stirling engine is illustrated in Figure 1. It consists of two constant volume processes and two isothermal processes. Heat is supplied to the working fluid as the fluid expands isothermally from point 3 to point 4 at a fixed temperature. The rejection of heat occurs during the process from point 1 to point 2 where the fluid is compressed isothermally at the lowest temperature of the cycle. The two reversible constant volume processes (i.e. process 4 to 1 and process 2 to 3) connect the two isothermals. The rejected heat during process 4 to 1 is used as a heat input to the fluid during process 2 to 3. Assuming that this phenomenon is ideal and reversible, the cycle may be said to operate at the Carnot efficiency. In order to achieve the Stirling cycle, a 100% efficient regenerator is required. The regenerator consists of a matrix/mesh of material which isolates the heat source from the heat sink, but at the same time allows the temperature to change gradually during the constant volume processes (McConkey and Eastop, 1993). The theoretical efficiency of a Stirling engine is that of the Carnot cycle, but in reality a well-designed engine can only reach between 40 to 70% of the Carnot efficiency (Walker, 1980).

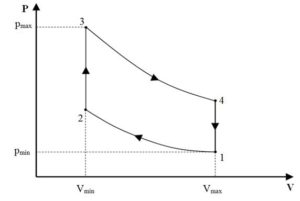
Figure 1- p-v Diagram of an Ideal Stirling Engine

Stirling engines are classified in three mechanical arrangements, alpha, beta and gamma. The alpha arrangement consists of two pistons placed in separate cylinders that are connected in series via a heater, regenerator and cooler. The beta and gamma arrangements consist of a displacer and a power piston. The displacer and the power piston in beta arrangement share the same cylinder; while in the gamma arrangement they have  separate cylinders (Urieli and Berchowitz, 1982), (Bapat, 2008). The main advantage of the alpha arrangement is the simple way in which it can be designed into a compact multiple cylinder engine which results in a high power output (Urieli and Berchowitz, 1982). In case of the beta arrangement, the advantage is that it has minimal dead volume, while the gamma configuration has rather large dead volumes which cause a reduction in power output cylinders (Urieli and Berchowitz, 1982).

In order to develop a low/medium Stirling engine, different analytical mathematical models can be used. Such models are discussed in this paper. Before discussing the mathematical models, the compression ratio which is a vital parameter is going to be defined.

The compression ratio is the ratio of the maximum volume to the minimum volume. According to Kolin (Kolin, 1991), in the case of the Stirling engine, the compression ratio varies between 1 and 2. Walker argues that the maximum compression ratio in such an engine can reach 2.5 (Walker, 1980). Trying to increase the compression ratio may result in having inadequate void volume in the heat exchanger. This may result in an inadequate heat transfer surface area and/or high pressure drops due to excessive aerodynamic drag losses (Walker, 1980). The compression ratio is given by the following equations:

In order to predict the performance of a Stirling engine, various mathematical models can be implemented. Usually the most popular models are subdivided into three orders; the first, second and third orders.

The first order model uses the Schmidt analysis in order to obtain initial sizing of the engine and includes experience factors to make up for the assumptions taken (Martini, 1980). This analytical approach is used at a preliminary stage in the design since it incorporates several assumptions such as isothermal working spaces and ideal heat exchangers. The Beale analysis method is another type of first order model used for preliminary engine design (Martini, 1983).

The second order model uses the Schmidt analysis, Finkelstein’s Adiabatic model or Philips’ semi-Adiabatic model and also considers engine losses (Martini, 1983).

The third order model is more extensive and is based on numerical analyses. This latter model is the most accurate of the three (Martini, 1980).

In the work for this paper, the first order model was used for the initial design of a model Stirling engine utilising atmospheric air as the working fluid. Microsoft Excel ® (2007) was used to mathematically model the relationships between the ratio of the displacer and power piston diameters (D_D/D_p), and phase angle (α) at different temperatures (ΔT) both against the work output per cycle. The Stirling engine efficiency was calculated using the Reitlinger theory. The Schmidt analysis which is based on the isothermal model is the simplest model, but is very helpful during the initial stages of the development of a Stirling engine. Using this analysis and if various losses are included, a reasonable accuracy in predicting the output power is achieved. The Schmidt model itself cannot predict the actual engine efficiency (Urieli and Berchowitz, 1982). The following are assumptions considered in the Schmidt analysis:

1. The working fluid in the expansion space and the heater is at the upper source temperature; whereas the working fluid in the compression space and the cooler is at the lower sink temperature.
2. Volumes of the working space vary sinusoidally.
3.  The expansion and compression processes are isothermal.
4. The heat exchangers and the regenerator are 100% effective.
5. There is no leakage of the working fluid i.e. constant mass of working fluid is assumed.
6. The equations of state for a perfect gas apply.
7. The rotational speed of the engine is uniform.
8. Steady state is established.
9. The potential and kinetic energy of the working fluid are neglected.
10. No pressure drops occur along pipes and ducts.

The Stirling engine is modelled by having individual components connected in series, these components are the compression space (c), the cooler (k), the regenerator (r), the heater (h) and the expansion space (e) (Figure 2 (D.G. Thombare, 2006)). The components considered in this model are treated as a homogenous entity where ‘m’ is the mass of the working fluid, ‘T’ is the absolute temperature and ‘V’ is the absolute volume of air in each component. (Urieli and Berchowitz, 1982)

Figure 2- Stirling Engine Model (Thombare, 20016)

Over one complete cycle the work done is given by Equation 5 (Martini, 1980) (Kolin, 1991):

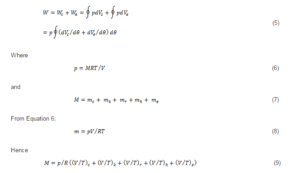
Where the temperature of the regenerator T_r can be defined in various ways according to the analytical correlation used. These definitions may be:

The work done over one complete cycle can be evaluated by both analytical correlations and/or by numerically methods. When solving numerically it can be shown that when the crank angle (θ) increment is 0.25°, there will be an error of 0.0003% in comparison with the analytical correlation developed byMayers’ (Martini, 1980). From the above analysis the power output can be calculated for a given R. P. M. In order to achieve more realistic results, the result can then be multiplied by experience factors such as those shown in Table 1 (Martini, 1980).

Table 1: Power Experience Factors (Martini, 1980)

Another method to establish the power output is by using the method developed by William Beale who based his method on experimental data available from various engine (Urieli and Berchowitz, 1982) s. Beale’s method resulted in equation 18 in which the Beale number, Be,  can be obtained from (Martini, 1983)..

The efficiency given by the first order model is equivalent to that obtained by Carnot. Again as in the case of the power output equation and in order to be more realistic, this efficiency is multiplied by some experience factors. Michels (Martini, 1980) points out that the brake efficiency is in the range of 46-69% of that given by Carnot’s equation, while Finegold and Vanderbrug concluded that the maximum brake efficiency is 52% of the Carnot one. The latter based their factor on the Philips Ford 4-215 engine. Martini (Martini, 1980) indicates that the maximum net brake efficiency is in the range of 38 — 65 % of the Carnot efficiency.

The Reitlinger theory provides another equation for calculating the Stirling engine efficiency. This is given in Equation 19. The Reitlinger theory considers also the efficiency of the regenerator, η_r (Kolin, 1991). When the regenerator efficiency η_ris equal to unity, then the engine’s efficiency becomes equal to that of the Carnot cycle.

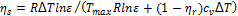
Schmidt Cycle Performance Analysis 

In this study a Schmidt cycle analysis was carried out for a gamma type engine having a fixed dead volume. Both a numerical approach and an analytical approach were used. Figure 3, Figure 4 and Figure 5 show the work done per a cycle at a temperature difference of 250°C, and at a fixed stroke of 24mm for three different phase angles i.e. 75°, 90° and 105°, respectively plotted against different diameter ratios, D_D/D_p.

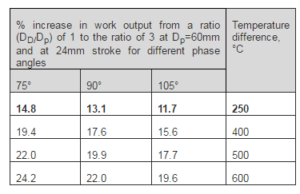
Note that the graphs are given for power piston diameter of 60, 80, 100, 150 and 200mm. From these graphs it can be noticed that when the power piston diameter increases, the work output also increases. This is due to more swept volume. The work output per a cycle for a fixed power piston diameter, D_p also increases as the ratio of the pistons (D_D/D_p) increases. But this is not as effective as increasing the power piston diameter. This gain is shown as a percentage in Table 3. One can note that the higher the temperature difference is, the higher will be the percentage increase in work output. Additionally the 75° phase angle exhibits the largest percentage gain in work output. This was followed by the 90° phase angle. Furthermore, the increase in the work per a cycle with respect to the diameter ratio is followed with a decrease in efficiency since the compression ratio is reduced (Figure 9).

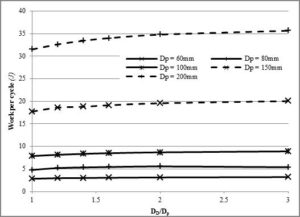
Figure 3- Work Done Per Cycle against Diameter Ratio at ΔT = 250°C (T_c = 50°C), Α = 75° and Stroke = 24mm 

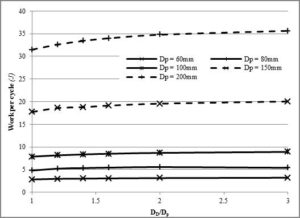
Figure 4- Work Done Per Cycle against Diameter Ratio at ΔT = 250°C (T_c = 50°C), Α = 90° and Stroke = 24mm 

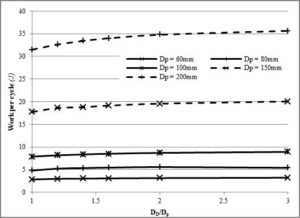
Figure 5- Work Done Per Cycle against Diameter Ratio at ΔT = 250°C (T_c = 50°C), Α = 105° and Stroke = 24mm

Table 2: Percentage Gain in Work Output from Diameter Ratio (D_D/D_p) Of 1 To 3

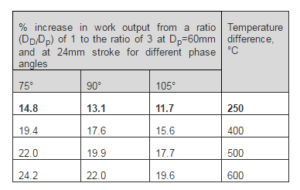
Furthermore, a case study was considered. For an operating temperature of an engine of 300°C and assuming a 50°C cold sink i.e. 250°C temperature difference, the compression ratio according to the empirical formula (Equation 7) shall be 1.23 if the stroke of the displacer and power piston is equal to 24mm, the ratio D_D/D_p should be equal to 2.1.

This compression ratio (ε=1.23) and temperature difference (250°C) give an efficiency of nearly 7% calculated using the Reitlinger equation with no regenerator. Note that the Carnot efficiency for a temperature difference of 250°C is 43.6%. From figure 4, for a 60 mm power piston diameter at 90° phase angle at 24mm stroke, the work per cycle is 3.18J for D_D/D_p =1.8 and 3.23J for D_D/D_p =2.1.

Figures 6, 7 and 8 illustrate the work per a cycle against the diameter ratio (D_D/D_p) at phase angles of 75°, 90° and 105° respectively at a fixed D_p=60mm and fixed stroke equal to 24mm for various temperature differences. It shows that the higher the temperature difference is, the higher is the work output. From these graphs it can be noticed that an enginewith ε=1.23 designed for low temperature differences, has the potential to produce more work output if higher heat sourcetemperatures are available. The percentage increase in work output for an increase in temperature difference for the subject case study (i.e. D_D/D_p= 2.1 at 90° phase angle at 24mm stroke) is shown in Table 3.

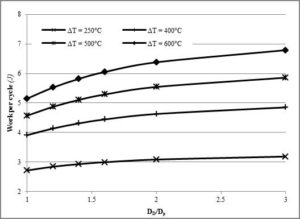
Figure 6- Work Per a Cycle against Diameter Ratio At Α = 75° and Stroke = 24mm for Various ΔT (250°C, 400°C, 500°C, 600°C) (T_c = 50°C)

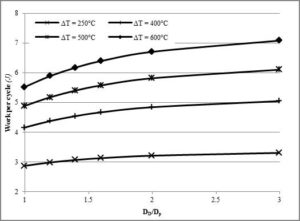
Figure 7- Work Per Cycle against Diameter Ratio at Α = 90° And Stroke = 24mm for Various ΔT (250°C, 400°C, 500°C, 600°C) (T_c = 50°C)

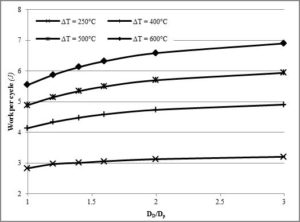
Figure 8- Work Per Cycle against Diameter Ratio at Α = 105° And Stroke = 24mm for Various ΔT (250°C, 400°C, 500°C, 600°C) (T_c = 50°C)

Table 3: Percentage Increase in Work Output W. R. T. Temperature Difference

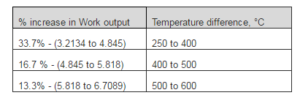
Figure 9 shows the variation of the Reitlinger efficiency with no regenerator plotted against the diameter ratio at different temperature differences. One can notice that the efficiency is more dependent on the diameter ratio, hence the compression ratio rather than the actual operating temperature difference. When increasing the operating temperature, one can expect an increase in work output but not an increase of the same magnitude in efficiency. This is especially the case at  large diameter ratios (D_D/D_p). Note that the operating temperature for the case study was 300°C at ΔT of 250°C (Excluding the use of the regenerator).

Figure 9- Reitlinger Efficiency with No Regenerator against Diameter Ratio (D_D/D_p) At Varies Temperature Difference

The analysis applied in the above case study is limited by the fact that the heat exchangers were assumed to be isothermal; whereas in reality they are more adiabatic. The various energy loss compnents, including the losses in fluid friction, mechanical losses, pressure drops, reheat loss and heat transfer losses were also ignored. This means that for the case study the output power is only a function of the volume, pressure and temperature difference.

In order to keep the optimum power output from an engine it should have some way of controlling the power output, these may be (Martini, 1980):

a)Increasing dead volume.

b)Varying the displacer/piston stroke.

c)Adding or removing working gas.

d)Changing the phase angle.

e)Temporary connecting the working space to a buffer space.

f)Varying the mean pressure within the expansion and compression space by varying the mass of the working fluid.

g)Increasing/decreasing the amount of heat input. 

Parabolic Trough and Heat Transfer Fluid Challenges

Market Availability

The solar energy collector plays an important part in the micro scale concentrated solar power system. During this study, surveys regarding the availability of parabolic troughs for domestic purposes (aperture diameter less than 1.6m) indicate only a couple of companies that can supply such collectors. To the authors’ best knowledge; the companies that can supply these parabolic troughs are Sopogy (Sopogy, 2011) and I.T collect (IT.Collect, 2011). Sopogy produces three different troughs, the Sopoflare which operates at a temperature of 121°C (aperture 0.76m), Soponova which operates at 270°C (aperture 1.65m) and Sopohelios which operates at 326°C (aperture 2.09m). I.T Collect produces a smaller scale trough operating at 250°C (aperture 0.5m). Both companies include single axis tracking in their product. A fundamental element of a parabolic trough system is the heat transfer fluid. When it flows through the receiver it absorbs the solar thermal energy concentrated by the collector. The fluid has an important role in a system because it determines important parameters such as operating temperature and the thermal storage technology that can be used.

Heat transfer fluid for concentrating solar power can be categorised as follows (Figure 10, Raada, J.W. and Padowitz, D. (2011):

1. Synthetic oil
2. Traditional salt
3. Advanced Heat transfer fluid (HTF)

Figure 10- Heat Transfer Fluid Categories with Respect to Their Operating Temperature (Raada, J. W. and Padowitz, D. (2011))

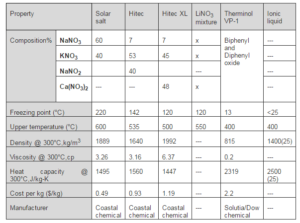
The most popular heat transfer fluid that is being used in concentrating solar power plants is synthetic oil. This high temperature oil is an organic substance consisting of a eutectic mixture of Biphenyl (C₁₂H₁₀ 26.5%) and diphenyl oxide (C₁₂H₁₀O 73.5%) having an operating temperature range between 12°C and 390°C. Two major companies that develop this type of heat transfer fluid are Soltuia Theminol and DOW under the trade names of VP-1 and Dowtherma-A, respectively (DOW, (2012)), ((Therminol, (2012)). The main limitations of such fluid are the cost, the operating temperature range and the relatively high vapour pressure. The latter limitation restricts the possibility for thermal storage medium because it will require special designed pressure vessels. A brief list of properties with respect to the mentioned brand names is found in Table 4.

Another category of heat transfer fluid is the traditional molten salts which are commercially available under the brand Hitec (Raada, J.W. and Padowitz, D. (2011)). The constituents of molten salts are a binary and also a ternary mixture of nitrates (NO₃) or/and nitrites (NO₂). Three types of molten salts are:

i.Solar salt (60%NaNO₃,40%KNO₃),

ii. Hitec (7%NaNO₃,53%KNO₃, 40%NaNO₂) and

iii. Hitec XL (7%NaNO₃,45%KNO₃, 48%Ca(NO₃)₂)

The three salts mentioned above exhibit many desirable heat transfer quantities at high temperature. They have high density, high heat capacity, high thermal stability, very low vapour pressure (ease of thermal storage) and low viscosity (low enough for sufficient pumpability) (Raada, J.W. and Padowitz, D. (2011)). Additionally, they are less expensive, non flammable and more environmental friendly when compared to synthetic oil. A drawback of such heat transfer fluid is their high freezing point which is typically in the range of 120-220°C (melting 240°C), depending on the mixture (Raada, J.W. and Padowitz, D. (2011)). This limit leads to an additional expenses resulting from further requirements such asanti-freeze systems and thicker insulation. Moreover, the fact of having a higher operating temperature implies an extra expense in specific materials, although it results in higher conversion efficiency. A patent for an advanced heat transfer fluid was made by Raade and Padowitz (Raada, J.W. and Padowitz, D. (2011)). They developed a fluid with a low melting point of 65°C and a thermal stability to at least 500°C. Furthermore, ionic liquid is being studied as another potential candidate for an advanced heat transfer fluid. A comparison of synthetic oil (VP-1), molten salts and Ionic liquid (omimBG4) (al., 2002) is illustrated in Table 4.

Table 4: Properties of Synthetic Oil, Molten Salts and Ionic Liquid (Raada, J. W. and Padowitz, D. (2011)), (Kearney, D. W.  (2001))

Introducing thermal energy storage in a system is not a new concept, but if a system is utilizing synthetic oil at an elevated temperature it exhibits high vapour pressure. Thus, in order to contain the oil, a pressure vessel would be required. This may be feasible for a domestic purpose system since the vessel capacity does not need to be too large as in the case of Megawatt-scale plants. Furthermore, the purpose of the storage pressure tank is mainly to cover periods of indirect sunlight rather than to operate during sunset hours. On the other hand, although molten salts have a negligible vapour pressure, they have a high freezing point which would add to the complexity of the plant. Such complexities include auxiliary heaters in the system.
 
Conclusions

The study reveals that developing a micro scale concentrated solar power system utilising a Stirling engine as the prime mover for electricity production offers a number of challenges. These challenges include the design of a low/medium temperature engine in order to match the power output to the available temperature source, the limited availability of solar energy collectors that can deliver heat to the engine by means of a heat transfer fluid at a temperature of at least 350°C and the feasibility of a thermal storage system to cover periods of low solar radiation levels. The largest challenge in the whole project is developing a low to medium temperature engine that can deliver electrical power at the best possible efficiency. One of the main drawbacks of a low/medium temperature engine is that it needs to be relatively large in size in order to generate enough energy to present a challenge to PV technology. The problem of size is also applicable to the sizing and procurement of the parabolic troughs that concentrate the sun’s energy on to the heat transfer fluid. This study has indicated areas of research aimed at developing a domestic solar thermal electricity system using a Stirling engine. As indicated in this paper there is a lack of information with respect to low/medium temperature Stirling engines especially when combined with parabolic trough collectors. A complete feasibility study of the system can only be performed once the Stirling engine acting as the prime mover is further developed using the best possible available technology. Each engine component, mainly the regenerator and heat exchangers, must be developed to their maximum efficiency. The design of these components is quite complex since the fluid flowing through the system is unsteady. Heat flow within the regenerator. and between the external heat source and heat sink in the heat exchangers depends on engine speed. Consequently, an iterative analysis is required. With the currently available mathematical models for brake power and efficiency prediction, it is evident that different engine configurations  (beta, gamma and alpha) require different experience or correlation factors in order to predict accurate values. This makes it quite challenging to design an engine solely on theoretical analysis in which a number of uncertainties are inevitable. The major implication of this study is that a joint theoretical and experimental approach is necessary in order to develop a domestic solar thermal electricity system using a Stirling engine coupled to parabolic trough collectors.

Nomenclature

References 

Bapat, S. L. (2008). ‘Stirling Engine, Indian Institute of Technology,’ Bombay, Presentation.
 
Coolenergy, (2011). ‘Solar Application,’ [Online], [Retrieved December 2011], http://www.coolenergyinc.com.
Publisher 
 
Daniel M. Blake et al. (2002). “New Heat Transfer and Storage Fluids for Parabolic Trough Solar Thermal Electric Plants,” 11th SolarPACES International Symposium on Concentrating Solar Power and Chemical Energy Technology.
Publisher – Google Scholar
 
DOW, (2012). DOW Chemical, [Online], [Retrieved January 2012], http://www.dow.com.
Publisher 

Eastop T. D. & McConkey, A. (1993). ‘Applied Thermodynamics for Engineering Technologists,’ 5th ed, Longman Group.
Google Scholar
 
Genoastirling, (2012). ‘The Engines,’ Available, [Online], [Retrieved February 2012], http://www.genoastirling.com.
Publisher 
 
Infinia, (2012). [Online] Available at: www.infiniacorp.com.
Publisher 
 
ITCollect, (2011). ‘Der Intelligente Kollektor,’ [Online], [Retrieved December 2011], http://www.it.collect.de.

Kearney, D., Herrmann, U., Nava, P., Kelly, B., Mahoney, R., Pacheco, J., Cable, R., Potrovitza, N., Blake, D. & Price, H. (2002). “Assessment of Molten Salt Heat Transfer Fluid in a Parabolic Trough Solar Field,” Journal of Solar Energy Engineering, 125 (2) 170-176.
Publisher 
 
Kearney, D. W. (2001). “Engineering Evaluation of a Molten Salt HTF in a Parabolic Trough Solar Field,” NREL Contract No: NAA-1-30441-04.
Publisher 
 
Kolin, I. (1991). ‘Stirling Motor: History – Theory – Practice,’ Dubrovnik University.
Google Scholar
 
Martini, W. R. (1980). ‘Stirling Engine Design Manual,’ 1st ed, Washington.
Google Scholar
 
Martini, W. R. (1983). Stirling Engine Design Manual, 2nd ed, Washington.
Publisher – Google Scholar
 
Microgen, (2012). Microgen Engine Corporation, [Online], [Retrieved February 2012], http://www.microgen-engine.com.
Publisher 
 
Raada, J. W. & Padowitz, D. (2011). “Development of Molten Salt Heat Transfer Fluid with Low Melting Point and High Thermal Stability,” Journal of Solar Energy Engineering, 133 (3) (6 pages).
Publisher – Google Scholar
 
Sopogy, (2011). ‘Solar Power Technology,’ [Online], [Retrieved November 2011] http://www.sopogy.com.
Publisher 
 
SunPower, (2012). Sun Power High Performance Free-Piston Stirling Engines, [Online], [Retrieved January 2012],http://www.sunpower.com.
Publisher 
 
Therminol, (2012). Heat Transfer Fluids, [Online], [Retrieved January 2012], http://www.therminol.com.
Publisher 
 
Thimsen, D. (2002). ‘Stirling Engine Assessment,’ Energy International, Inc., Bellevue, Technical Report 2002.
Google Scholar

Thombare, D. G. & Verma, S. K. (2008). “Technological Development in the Stirling Cycle Engines,” Renewable and Sustainable Energy Reviews, 12 (1) 1-38.
Publisher – Google Scholar
 
Urieli, I. & Berchowitz, D. M. (1982). Stirling Cycle Engine Analysis, Adam Hilger Ltd.
Publisher – Google Scholar 
 
Walker, G. (1980). Stirling Engines, Oxford University Press.
Publisher 
 
Whispergen, (2012). ‘Stirling Engine,’ [Online], [Retrieved January 2012], http://www.whispergen-europe.com.