N-Pentane – Limonene Mixtures as Working Fluids for Organic Rankine Cycles

Introduction

Operation of binary-cycle power plants depends on different factors such as the chemical and physical features of the geothermal fluid used in the primary energy-conversion stage, nature of the working fluid in the secondary stage, equipment, and local environmental features of the plant site.

The selection of the working fluid is of utmost importance in designing an organic Rankine cycle (ORC). Fluid properties such as thermodynamic, chemical stability, safety and environmental aspects must be considered.

The use of zeotropic mixtures rather than single component working fluids has long been considered, mainly from a thermodynamic point of view (Iqbal, et al. 1976, Iqbal and Starling 1976, Angelino and Colonna di Paliano 1998, Wang, et al. 2010, Aghahosseini and Dincer 2013, Weith, et al. 2014), but also from the stand point of thermo-economics (Calm and Hourahan 2011, Heberle and Brüggemann 2016, Sarkar 2016, Astolfi et al. 2017).

ORC rigs are closed loops, but nevertheless daily losses of the organic fluid occur. For example, Moya and DiPippo (2007) have reported that 29 kg of n-pentane (n-C₅H₁₂) are lost to the environment daily, in the Unit 5 bottoming binary plant at Miravalles geothermal field in north-western Costa Rica. One thought of identifying a renewable source for an organic liquid that would offer trade-offs between thermodynamic performance and environmental suitability, when forming part of zeotropic n-C₅H₁₂ – “other component” working mixtures that offer a significant eco-friendly benefit.

Limonene was determined as a possibility, due to the local production of orange essential oil from which the diterpene limonene could be isolated on an industrial basis. Besides potential new value chains, it is expected that the use of n-C₅H₁₂ – limonene mixtures implies neither significant externalities associated to stratospheric ozone depletion nor contribution to global warming. In ecological eventualities such as massive spills, this renewable substance is readily biodegradable (41% – 98% degradation by biochemical oxygen demand in 14 days) under aerobic conditions in a standard test (Filipsson, Bard and Karlsson, 1998).

Modelling the performance of the working fluid mixtures in a certain setup can certainly give answers to technical scenarios, but we present here simple laboratory evaluations useful to carry out, prior to extensive computer modelling about mixed ORC working fluids.

Statement of the Proposal

It is important to have data that allow numerical estimations of condensation temperatures of gas-phase mixtures, to intuit whether at the outlet of a turbine, the fluid may behave as dry, isentropic or wet because the first two conditions pose a minimum problem in preventing erosion and damage of turbine blades, due to liquid droplet impingement in the blades during expansion.

A model calculation can be carried out by assuming the mixed liquids obey Trouton’s rule (entropy of vaporisation, Δ_vapS ~ 90 J K^-1 mol^-1):

The value of enthalpy of vaporisation (Δ_vap H) can be obtained from the thermal cubic-expansion coefficient (α) of the liquid mixtures, through the so-called soft-solid model for liquids (Castellón-Elizondo, et al. 2006). For simple molecules, the following relation between α and Δ_vapH holds:

Acceptable estimations for Δ_vapH are obtained in kJ mol^-1. Once T_boil is obtained for every mixture, it can be taken as the low temperature of the heat sink. Thus, Carnot efficiency is calculated as

η (Carnot) can be used as benchmark, before extensive thermodynamic model calculations are carried out.

Materials and Methods

Materials

n-Pentane, isopentane and limonene were obtained from Sigma-Aldrich, and used without any further treatment.

Physical properties of mixtures

α values were determined from the densities of the mixtures (ρ) at different temperatures by pycnometry, as described in standard textbooks of experimental analytical or physical chemistry. The best regression linear equations of lnρ vs. T give α = – (¶lnρ/¶T)_p. Measurements were done by triplicate, and average quantities include standard deviations from the mean.

Rates of evaporation were determined gravimetrically by following mass (m) loss of samples contained in open Petri dishes under controlled laboratory conditions at 22 °C and 87 kPa, and in the absence of air currents. The loaded dishes were placed on an analytical balance pan, and the mass losses followed along time. The balance lateral lids were closed, leaving the upper lid open to prevent saturation of the space over the liquid. For mixtures, the time – mass data were conveniently fitted to cubic polynomials, and initial rates of evaporation calculated as:

Results and Discussion

Volatility considerations

Leakage of organic working fluids poses a steady environmental risk, although substances such as n-C₅H₁₂ (normal boiling point = 36 °C) or isopentane (i-C₅H₁₂, normal boiling point = 26 °C) have relative low environmental effect (global warming potential = 5) (Calm and Hourahan, 2011) and null ozone depletion potential. The incorporation of limonene (normal boiling point = 176 °C) in the composition of working fluid aims to the reduction of the magnitude of leakage. Thus, the first issue to be considered is the volatility of mixtures at room temperature, say laboratory conditions at 22 °C.

The rate of isothermal evaporation of pure liquids follows zero-order kinetics, and is described at the molecular level by the Hertz-Knudsen equation:

where p_v is the vapour pressure of the liquid substance, M its molar mass and the rest of symbols have their usual meaning. κ is the so-called evaporation coefficient, a correction for non-ideal chemical behaviour. Hołyst et al. (2015) have challenged the H-K equation on grounds that “… may not appropriately grasp the physical mechanism of evaporation”. The authors propose that a very small difference between the vapour pressure and the liquid pressure is the most probable driving force for evaporation of liquids. Their model implies that the pressure difference equals to the momentum flux of the leaving molecules (momentum associated to the molecules leaving the liquid surface whilst the phase change takes place). Nevertheless, their mechanistic proposal is corresponding to the straightforward molecular interpretation of the H-K equation.

Liquid-mixture evaporation deviates from linear kinetics. The rate of evaporation decreases as the less volatile components accumulate in the remaining liquid phase. Thus, a kinetic parameter such as initial rate of evaporation expressed in mass units such as kg s^-1 m^-2 must be used, because the gaseous phase is composed of the different chemical species and the rate changes during the process.

Figure 1 shows the time profile for the evaporation of n-C₅H₁₂ and a mixture with the alkane mass fraction (x) of 0,43.

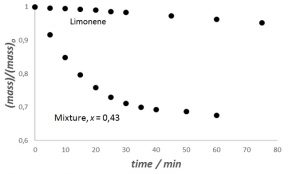
Figure 1: Time profile for the evaporation of limonene and a 43% (by mass) mixture

of n-C₅H₁₂ –

limonene, at 22 °C and 87 kPa

Non-ideal mixtures (Raoult’s law not obeyed) may show evaporation rates (vapour pressures) that are faster or slower than either of the pure components. Table 1 and figure 2 give the evaporation rates of mixtures, obtained by differentiation of the best cubic-fit polynomial for the mixtures studied, as explained above.

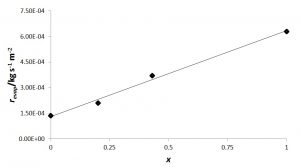
Figure 2: Evaporation rates of n-C₅H₁₂ – limonene mixtures as function of mass fraction of the alkane at 20 °C and 87 kPa atmospheric pressure 

Table 1: Evaporation rates of n-C₅H₁₂ – limonene mixtures as function of mass fraction of the linear alkane at 20 °C and 87 kPa atmospheric pressure

A linear dependence is observed that fits acceptably (r_p² = 0,99) the regression equation

r_evap / kg s^-1 m^-2 = 1,3 × 10^-4 + 5,0 × 10^-4 × n-C₅H₁₂ mass fraction                                      (6)

Since i-C₅H₁₂ is more volatile than the linear hydrocarbon isomer, one thought interesting to measure the evaporation kinetics of i-C₅H₁₂ – limonene-rich mixtures, to learn whether a linear x – r_evap relationship also existed. Table 2 gives the results for eight such mixtures.

Table 2: Evaporation rates of i-C₅H₁₂ – limonene mixtures as function of mass fraction of the branched alkane at 22 °C and 87 kPa atmospheric pressure

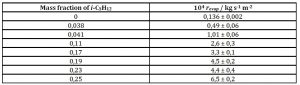
A linear dependence is also observed that fits acceptably (r_p² = 0,94) the regression equation

r_evap / kg s^-1 m^-2 = -7,8 × 10^-6 + 2,3 × 10^-3 × i-C₅H₁₂ mass fraction                                        (7)

The empirical result suggests that both mixtures behave next to ideally, despite the differences in molecular size and shape of the components. Non-associated liquids form approximately ideal mixtures if their Hildebrand solubility parameters differ by small amounts (Hildebrand and Scott, 1964). The values for i-C₅H₁₂, n-C₅H₁₂ and limonene are 13,8 (J cm^-3)^½, 14,4 (J cm^-3)^½ and 16,4 (J cm^-3)^½, respectively. The values are close enough to render the chemical behaviour as ideal-like. Thus, if the degree of ideality of these mixtures is considerable, an approximately linear relationship is expected to exist between vapour pressure and composition (compliance with Raoult’s law). Since the evaporation rate varies proportionally to the vapour pressure of the liquid, the linearity observed between r_evap and composition is understood.

According to the regression equations, for a n-C₅H₁₀ – limonene mixture with 20% of limonene, there is a 16% decrease in the rate of evaporation at 22 °C and 87 kPa, relative to the pure hydrocarbon. For the case of i-C₅H₁₀, a 20% decrease in r_evap is to be observed, under the same conditions.

Another advantage of limonene is its flash point (Fp) of 48 °C, relative to the same parameter for n-C₅H₁₂ (-49 °C) and i-C₅H₁₂ (-51 °C).

By interpolation, r_evap can be calculated as 5,3 × 10^-4 kg s^-1 m^-2 for a mixture of n-C₅H₁₂ containing 20 % limonene. Our experimental value for n-butyl acetate at 22 °C and 87 kPa of 4,89 × 10^-5 kg s^-1 m^-2 yields r_evap (AcOBu = 1) = 11. This value allows the estimation of Fp equal to -18 °C (Mata-Segreda, 2017 unpublished results). For the case of an i-C₅H₁₂ analogous mixture, the expected value is -14 °C. This effect shows a safety advantage for the mixtures, over the use of pure alkanes.

Thermal Efficiency

Enthalpies of vaporisation can be estimated from the coefficient of thermal cubic expansion of liquids, as indicated in the Materials and methods section.

Figure 3 and table 3 give the enthalpies of vaporisation as function of composition for n-C₅H₁₀ – limonene mixtures, by using the general relationship between α and Δ_vapH indicated by equation (2). Table 4 gives the enthalpies of vaporisation for i-C₅H₁₀ – limonene mixtures.

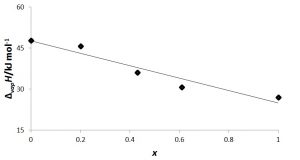
Figure 3: Enthalpies of vaporisation of n-C₅H₁₂ – limonene mixtures as function of mass fraction of the alkane at 22 °C and 87 kPa atmospheric pressure 

Table 3: Enthalpies of vaporisation of n-C₅H₁₂ – limonene mixtures as function of mass fraction of the alkane at 22 °C and 87 kPa atmospheric pressure 

As expected from the previous kinetic results shown above, this linear regression also gives a relationship between heat of vaporisation and composition, at an acceptable degree of significance (r_p² = 0,96):

Δ_vapH / kJ mol^-1 = 48 – 23 × n-C₅H₁₀ mass fraction                                                             (8)

The values for pure n-C₅H₁₂ and limonene are somehow deviant from the data obtained from the well-known collection of Chickos and Acree, Jr. (2003): 26 kJ mol^-1 and 46 kJ mol^-1, respectively but the aim of this experiment holds from a semiquantitative point of view.

Table 4 gives the corresponding values for the i-C₅H₁₀ – limonene mixtures.

Table 4: Enthalpies of vaporisation of i-C₅H₁₂ – limonene mixtures as function of mass fraction of the alkane at 22 °C and 87 kPa atmospheric pressure

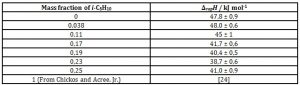
The linear relationship is also qualitatively satisfactory (r_p² = 0,96) for i-C₅H₁₂:

Δ_vapH / kJ mol^-1 = 47 – 23 × i-C₅H₁₀ mass fraction                                                              (9)

Taking the Miravalles Unit 5 as model (Moya and DiPippo, 2007), Carnot efficiencies are calculated for 20% limonene mixtures by using the temperature of the residual brine (heat source) as 147 °C, and the lower temperatures are the corresponding boiling point of the mixtures.

If n-C₅H₁₂ is used at a level of 80% by mass, Δ_vapH = 29,6 kJ mol^-1, T_boil = 329 K and η (Carnot) = 0,22. The case for i-C₅H₁₂ results as Δ_vapH = 28,8 kJ mol^-1, T_boil = 320 K and η (Carnot) = 0,24.

The Carnot efficiency of Miravalles Unit 5 is set by the heat-source temperature of 147 °C and the waste heat given off at 38 °C. Thus, η (Carnot) = 0,26, but the actual thermal performance is 15%, due to the internal irreversibilities of the rig. Nevertheless, the use of limonene in mixtures of either of the two pentanes suggests that a complete thermodynamic analysis is valuable to carry out.

Conclusion

Mixtures of n-C₅H₁₂ or i-C₅H₁₂ with up to 20% of limonene by mass may be considered for extensive thermodynamic evaluation as working fluids in ORC operations, because their volatility implies acceptable Carnot efficiencies as benchmark for further thorough model studies. Environmental and safety aspects of their use and storage are better than for the two pure hydrocarbons.

Acknowledgements

The authors wish to thank Evaristo Rodríguez (ICE) for his interest on this study. MS-G acknowledges an internship at IC-ICE.

References

Aghahosseini, S. and Dincer, I. 2013. Comparative performance analysis of low-temperature organic Rankine cycle (ORC) using pure and zeotropic working fluids. Applied Thermal Engineering 54, 35-42.

Google Scholar

Angelino, G. and Colonna di Paliano, P. 1998. Multicomponent working fluids for organic Rankine cycles (ORC). Energy 23, 449-463.

Google Scholar

Astolfi, M., Martelli, E. and Pierobon, L. 2017. Thermodynamic and technoeconomic optimization of organic Rankine cycle systems. In E. Macchi and M. Astolfi, eds. Organic Rankine cycle (ORC) power systems. Technologies and applications, Elsevier/Woodhead Publishing: Amsterdam, chapter 7.

Calm, J. M. and Hourahan, G. C. 2011. Physical safety, and environmental data for current and alternative refrigerants. 23^rd International Congress of Refrigeration, 21-26 August, Prague, ID:915.

Google Scholar

Castellón-Elizondo, E., Lutz, G. and Mata-Segreda, J. F. 2006. The soft-solid model for liquids. Application to biodiesel and other materials of technological interest. Journal of Physical Organic Chemistry 19, 744-747.

Google Scholar

Chickos, J. S. and Acree, Jr., W. E. (2003). Enthalpies of vaporization of organic and organometallic compounds, 1880-2002. Journal of Physical Chemistry Reference Data 32, 519-878.

Google Scholar

Filipsson, A. F., Bard, J., and Karlsson, S. (1998). Concise international assessment chemical assessment document 5. Limonene. Published under the joint sponsorship of the United Nations Environment Programme, the International Labour Organisation, and the World Health Organization, and produced within the framework of the Inter-Organization Programme for the Sound Management of Chemicals.

Heberle, F. and Brüggemann, D. 2016. Thermo-economic analysis of zeotropic mixtures and pure working fluids in organic Rankine cycles for waste heat recovery. Energies, 9, 226-242.

Google Scholar

Hildebrand, J. H., Scott, R. L. 1964. The solubility of nonelectrolytes (3^rd edition), Dover, p. 211.

Hołyst, R., Litniewski, M. and Jakubczyk, D. (2015). A molecular dynamics test of the Hertz-Knudsen equation for evaporating liquids. Soft Matter 11, 7201-7206.

Google Scholar

Iqbal, K. Z., Fish, L. W. and Starling, K. E. 1976. Advantages of using mixtures as working fluids in geothermal binary cycles. Proceedings of the Oklahoma Academy of Science 56, 110-113.

Google Scholar

Iqbal, K. Z. and Starling, K. E. 1976. Use of mixtures as working fluids in ocean thermal energy conversion cycles. Proceedings of the Oklahoma Academy of Science 56, 114-120.

Google Scholar

Mata-Segreda, J. F. 2017. The concentration of vapour of flammable and combustible liquids over the liquid surface increases with temperature. Since flash point (Fp) is the minimum temperature at which vapours kindle prompted by an ignition source, there should be a negative correlation between this parameter and vapour pressure. By extension, such relationship may be extended to r_evap. An empirical relationship is known indeed between Fp and log r_evap: Durkee II, J. B. 2014. Cleaning with solvents: Science and technology, WA/Elsevier: Amsterdam, chapter 9, p. 302. Our empirical equation is Fp / °C = 21 – 39 × log r_evap (AcOBu = 1), obtained from the data of 119 organic liquids of different molecular nature.

Moya, P. and DiPippo, R. 2007. Unit 5 bottoming binary plant at Miravalles geothermal field, Costa Rica: Planning, design, performance and impact. Geothermics 36, 63-96.

Google Scholar

Sarkar, J. 2016. Comprehensive study on the role of eco-friendly working fluid properties on ORC performances. International Journal of Thermodynamics 19, 198-204.

Google Scholar

Wang, J. L., Zhao, L. and Wang, X. D. 2010. A comparative study of pure and zeotropic mixtures in low-temperature solar Rankine cycle. Applied Energy 87, 3366-3373.

Google Scholar

Weith, T., Heberle, F., Preißinger, M. and Brüggemann, D. 2014. Performance of siloxane mixtures in a high-temperature organic Rankine cycle considering the heat transfer characteristics during evaporation. Energies 7, 5548-5565.

Google Scholar