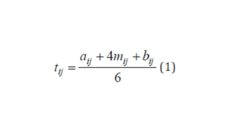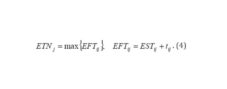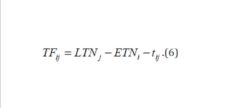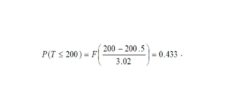Introduction
Project management is nowadays a widely used and discussed discipline. This fact is substantiated by numerous scientific articles, books and publications dealing with these problems (Berganitiños and Vidal-Puga, 2009; ÄŒerná, 2008). This discipline is also included in the courses of numerous faculties focusing on economy both in the Czech Republic (International project management association, 2011) and abroad. Experts are also associated in various professional organizations or associations (Korecký and Trkovský, 2011; Společnost pro projektové řízení ÄŒeská republika, 2011).
Project managers and other members of the project team use different approaches to solve PERT method (Doskočil and Doubravský, 2012; Seal, 2001). These approaches are based on various methods (Hajdu, 2013; Hashemin, Ghomi and Modarres, 2012; Yaghoubi et al, 2011) for calculating the variation of nodes. This fact causes a difference in the results of probabilistic analysis of the project (Doskočil and Doubravský, 2013). Some papers show another approach to analyze the critical paths in a project network with fuzzy activity times. It is a used method of fuzzy numbers (Relich, 2013), where the activity time is represented by a triangular fuzzy number. This method is compared with classical CPM and PERT methods.
The paper deals with a PERT method. This method is signed as stochastic method. Its aim is an identification of critical path in a chart. The chart represents a model of a project. The implementation of the PERT algorithm is based on the critical path method-CPM (Trietsch and Baker, 2012). The paper focuses on the comparison of two different approaches (deterministic approach, Monte Carlo method), calculation of probability analysis and their influence on the calculation of the planning time of the project and their probabilities.
Materials and Methods
PERT Method
Three estimates of activity duration were provided: optimistic, most likely and pessimistic. Subsequently, activity duration mean times (1) were computed according to the following formula (Relich, 2010; Plevný and Žižka, 2005):
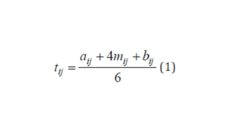
Where:
tij — activity duration,
aij — optimistic estimate of activity duration,
mij – most likely estimate of activity duration,
bij — pessimistic estimate of activity duration.
Variances (2) and standard deviations (3) of activity duration were also calculated. The following formulas were used for their calculation:

For the purposes of the time analysis, basic characteristic times were calculated in accordance with traditional approaches. For more detailed information see related publications (ÄŒerná, 2008; Wisniewski, 1996).
Using incidence matrix, the earliest times for each node (4) were calculated as follows:
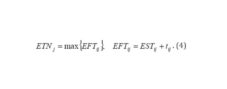
Where:
ETNj – Earliest Time of Node,
EFTij – Earliest Finish Time of Activity,
ESTij – Earliest Start Time of Activity,
tij – Activity Duration.
The latest times for each node (5) were calculated as follows:

Where:
LTNi – Latest Time of Node,
LFTij – Latest Start Time of Activity,
LFTij – Latest Finish Time of Activity,
tij – Activity Duration.
The total float of activity (6) from ith node to jth node was calculated as follows:
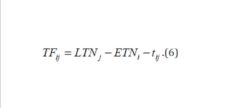
Where:
ETNi – Earliest Time of Node,
LTNj – Latest Time of Node,
tij – Activity Duration.
Monte Carlo Method
Monte Carlo method is a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo method is often used in simulations of mathematical and economical systems (it is used to model phenomena with significant uncertainty in inputs, such as the calculation of risk in business). This method is most suited to calculation by a computer (Salling and Leleur, 2011). It can be used when it is infeasible to compute an exact result with a deterministic algorithm (Vose, 2008).
Results
Case study describes a project which includes 18 subactivities. The details of the activities and their predecessor relationships are presented in column 1 and 2 of Tab. 1. The details of the activities and time estimates, i.e. optimistic (aij), most likely (mij) and pessimistic (bij) of activity duration are shown in row 3, 4 and 5, see Tab. 1.
Table 1: Representation of the project (Source: Edited by (Rais and Doskočil, 2011))

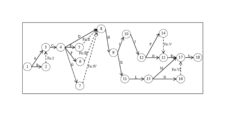
The graphical representation of predecessor and relationships of project (the network chart) is shown in Fig. 1. Network chart consists of 18 nodes, 18 real activities and 6 fictions activities. All calculations were computed using own programs creating in MS Excel.
Figure 1: Network chart (Source: Own work)
Approach I: PERT Method
Table 2 presents information about the project, see column 1—3. The calculated expected value of the activities is in column 4 and their variances are in column 5. Column 6 to 10 represents information about the times characteristics of activities.
Table 2: Calculation of Activity Duration Mean Time and Activity Variance (Source: Own work)
The last column of table 2 contains the total float of activities, which identifies the critical path. The total float equals zero for the following activities: (1;2), (2;3), (3;4), (4;8), (8;9), (9;10), (10;12), (12;15), (15;17) and (17;18). These activities are therefore critical, and their sequence determines the probable critical path. The estimate of the project duration mean time equals the critical path duration, i.e. 200.5 time unit.
Approach II: Monte Carlo Method
Table 3 presents the solving of the same case study which is calculation using Monte Carlo methods. For each simulation there is time duration of the project in the last row.
Table 3: First 10 simulations of the Monte Carlo method (Source: Own work)
Discussion
In this part the results of probability calculation of completion of the project are presented for PERT method (Mathews, 2005; Novotná, Kříž, 2012) and Monte Carlo method. Planning time 200 (time units) was determined for both approaches.
|
The value of probability for PERT method is:
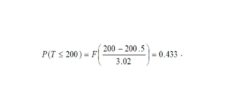
|
The values of probability for Monte Carlo method are seen in Tab. 4.
Table 4: Calculated probabilities and result of the test (Source: Own work)

The values of the calculated probabilities for Monte Carlo method are in 3 row of Tab. 4. In order to compare the values in this row with probability value of PERT method (0.433), the application of the test about parameter p (alternative distribution) would be useful. The null hypothesis of the test may be formulated: Different of probabilities (between PERT method and Monte Carlo method for each simulation, see Tab. 4) is not statistically significant. An alternative hypothesis is as follows: the different of probabilities is statistically significant. For the selected level of importance α = 0.05 the test criterion are calculated, see e.g. 4 row of Tab. 4. As these values are greater than critical value 1.96, we reject the null hypothesis (row 5), and accept the alternative hypothesis. That means that the differences are statistically significant.
Conclusion
The paper deals with a time and probability analysis in stochastic chart PERT. The paper focuses on the comparison of two different approaches (PERT method and Monte Carlo method) calculation for probability analysis. Concretely, the planning time of the project was calculated. A sample network chart was examined and contains 18 nodes and 18 real activities and 6 fictions activities. For the purpose of the analysis, the basic time characteristic were calculated in accordance with traditional approaches related to the PERT method.
The scientific aim of the paper is the comparison of two different approaches calculation of the probability of completion of the project. For this reason, project duration and the standard deviation of the project was calculated by the classical method. Then, the planned date of completion of the project was selected at 200 time units. Based on the duration and the standard deviation of the project, the probability of completion project till 200 time units was determined.
Then the duration of the project was determined using the Monte Carlo method and the probability of completion project till 200 time units was determined. Because the Monte Carlo method belongs to simulation methods, the results were successively obtained for 10, 100, 300, 500, 1000, 5000 and 10000 simulations (iterations). Since the calculation of the probability of project completion to 200 time units is based on using the normal distribution, values were generated using the normal distribution in the Monte Carlo method. The calculated probabilities of project completion were compared using statistical hypothesis testing.
The assumption was expressed: The difference between the results obtained by the Monte Carlo method and PERT method is not significant with increasing number of simulations (iterations). For this reason the hypothesis was formulated: The results (probabilities) are not statistically significant. For testing the significance of difference between the calculated probabilities, the test of parameter p for alternative distribution was used. The null hypothesis was formulated: There is no statistically significant difference between the calculated probabilities, i.e. both approaches are identical from an application point of view. Opposite the null hypothesis, the alternative hypothesis was formulated: there is a statistically significant difference between the calculated probabilities. This null hypothesis was rejected for all testing. It follows that there is a difference between the approaches (it depends whether we use a PERT method or Monte Carlo method).
Acknowledgments
This paper was supported by grant FP-S-13-2148 ‘The Application of ICT and Mathematical Methods in Business Management’ of the Internal Grant Agency at Brno University of Technology.
References
1. Berganitiños, G. and Vidal-Puga, J. (2009), ‘A Value for PERT Problems’, International Game Theory Review, 11(4), 419—436.
Publisher – Google Scholar
2. ÄŒerná, A. (2008), Metody operačního management (Methods of Operational Management), Oeconomica, Praha.
3. Doskočil, R. and Doubravský, K. (2012), ‘Implementation of the PERT Method in MS Excel’, Proceedings of the 18th Inernational Business Information Management Association (IBIMA), ISBN: 978-0-9821489-7-6, 9—10 May 2012, Istanbul, Turkey, 1262—1271.
4. Doskočil, R. and Doubravský, K. (2013), ‘Risk Analysis of Stochastic PERT Graph’, Trends Economics and Management, 7(14), 35—43.
Google Scholar
5. Hajdu, M. (2013), ‘Effects of the application of activity calendars on the distribution of project duration in PERT networks’. Procedia — Social and Behavioral Science, 119, 776—775.
Publisher – Google Scholar
6. Hashemin, S. S., Ghomi, F. and Modarres, M. (2012), ‘Optimal constrained non-renewable resource allocation in PERT networks with discrete activity times’, Scientia Iranica, 19(3), 841—848.
Publisher –
7. International project management association. (2011) [Online], [Retrieved December 6, 2012], http://ipma.ch/.
8. Korecký, M. and Trkovský, V. (2011), Management rizik projektu se zaměřením na projekty v průmyslových podnicích (Management of project risks, focusing on projects in industrial companies), Grada Publishing, Praha.
9. Mathews, P. (2005), Design of Experiments with Minitab, ASQ Quality Press, Milwaukee.
Google Scholar
10. Novotná, V. and Kříž, J. (2012), ‘The Impact of ICT level on the value of regional GDP in the regions of the Czech Republic’, Proceedings of the 19th Inernational Business Information Management Association (IBIMA), ISBN: 978-0-9821489-8-3, 12—13 November 2011, Barcelona, Spain, 516—526.
11. Plevný, M. and Žižka, M. (2005) Modelování a optimalizace v manažerském rozhodování (Modelling and Optimization in Managerial Decision Making), Západočeská univerzita v Plzni, Plzeň.
12. Rais, K. and Doskočil, R. (2011) Operační a systémová analýza I (Operational and System Analysis I), Brno University of Technology, Faculty of Business and Management, Brno.
13. Relich, M. (2010), ‘Assessment of task duration in investment projects’, Management, 14(2), 136—147.
Google Scholar
14. Relich, M. (2012), ‘An evaluation of project completion with application of fuzzy set theory’, Management, 16 (1), 216—229.
Publisher – Google Scholar
15. Salling, K. B. and Leleur, S. (2011), ‘Transport appraisal and Monte Carlo simulation by use of the CBA-DK model’, Transport Policy, 18(1), 236—245.
Publisher – Google Scholar
16. Seal, K. C. (2001), ‘A Generalized PERT/CPM Implementation in a Spreadsheet’, INFORMS Transaction of Education, 2(1), 16—26.
Publisher – Google Scholar
17. Společnost pro projektové řízení ÄŒeská republika (Project Management Company Czech Republic). (2011) [Online], [Retrieved June 15, 2013], http://www.cspr.cz/.
18. Trietsch, D. and Baker, K. R. (2012), ‘PERT 21: Fitting PERT/CPM for use in the 21st century’, International Journal of Project Management, 30(4), 490—502.
Publisher – Google Scholar
19. Vose, D. (2008), Risk Analysis, A Quantitative Guide, John Wiley & Sons.
Google Scholar
20. Wisniewski, M. (1996), Metody manažerského rozhodování (Methods of Managerial Decisions), Grada Publishing, Praha.
21. Yaghoubi, S., Noori, S., Azaron, A., and Tavakkoli-Moghaddam, R. (2011), ‘Resource allocation in dynamic PERT networks with finite capacity’, European Journal of Operational Research, 215(3), 670—678.
Publisher – Google Scholar