Introduction
Pricing models pursue four goals (Jorgensen 1986; Winer, 2005; Rao and Kartono, 2009): (1) they describe in which environment a pricing policy takes place, (2) they explain how pricing policies are shaped, (3) these models offer pricing rules or principles to decision makers, (4) they try to predict sales, pricing policies and the resulting profits in different scenarios.
Most of these models are developed in a static setting. The static setting, though useful, does not capture the richness of real effects (Tirole, 1988). In particular, it can highlight certain equilibria but gives no idea of their stability or speed of convergence. In addition, such models do not characterize the price dynamics and sales of a product during its life cycle (Jorgensen et al., 2007). To address these shortcomings, several models have been developed in management science to explicitly include the dynamic or intertemporal element in the study of pricing policies (Kalish, 1983; Dockner et al., 2000).
The models that best explain pricing originate in three main areas of the literature: dynamic economics, new product diffusion, and non-cooperative game theory. Dynamic economics, whose roots date back to Evans’s (1924) Dynamics of the Monopoly, provided the fundamental models and tools for pricing in an intertemporal framework. The new product diffusion models that were developed in management science, especially since Bass (1969), emphasize the impact of production externalities and diffusion effects on sales of a given product. Non-cooperative game theory makes it possible to model and understand strategic interactions between market players (Jorgensen, 1986).
Pricing models are structured around a product’s life cycle (Dockner et al., 2000). The choice of prices by the firm impacts its sales and therefore its profits (Mahajan et al. 1990; Jorgensen and Zaccour, 2004). Thus, it is interesting to characterize the pricing policies of the profit-maximizing firm, based on assumptions of consumer and firm behavior. In that sense, pricing models pursue a normative goal (Mahajan et al., 2000). Normative rules can be analytically or numerically founded. Analytical results are preferable because they are more general. However, it is not always possible to obtain them due to the problem’s complexity. Simulation may be necessary to understand a model’s characteristics (Jorgensen et al., 2007).
Several articles lay the foundations of dynamic pricing. Evans (1924) is the first study on dynamic pricing. It addresses the existence of an equilibrium. Roos (1925) generalizes the previous work to duopolies. Bass (1969) provides the first diffusion model for durable goods. Robinson and Lakhani (1975) studied dynamic pricing numerically, integrating diffusion effects. Kalish (1983) characterizes analytically the different pricing policies for different types of dynamic effects. Dockner and al. (2000) build on this approach, in an oligopolistic setting. Chatterjee (2009) and Seetharaman (2009) offer reviews of the recent literature on the subject.
In this survey of the literature, we shall detail in the first section the principles of dynamic pricing. In the second section, we shall outline the fundamentals of pricing. The third section presents the monopolistic, and the fourth section the competitive cases. The fifth section identifies the main extensions to these models. The sixth section concludes.
Principles of Dynamic Pricing
Pricing is the process of setting the price for a good or a service. “Dynamic” or “intertemporal” refers to the consideration of time in the analysis. Dynamic pricing therefore concerns the pricing of a product over time.
Dynamic Effects
Learning
As more and more units of a certain product are produced, observation shows that current productivity is linked to past production. In other words, productivity depends on past experience in the production of that particular good. This intuition is modeled by taking past production volumes as a proxy for accumulated experience (Arrow, 1962). Learning by doing implies that productivity increases with cumulative production. This increase in productivity is reflected in the decrease of unit production costs. Note that in an oligopoly setting, an interesting phenomenon is the appropriation of learning by other firms. It is the spillover effect of learning (Dockner et al., 2000).
Diffusion Effects
Diffusion effects are all the phenomena related to a higher market penetration that affect the probability of purchase. These phenomena include: greater knowledge of the market through word-of-mouth, self-advertisement of the product, uncertainty reduction due to a better reputation of the product (Bass, 1969; Rao and Kartono, 2009).
Word-of-mouth is an emulation effect. It is an internal influence on sales. It is linked to social interactions of past buyers who contribute to the product’s reputation. The more a product sells, the stronger word-of-mouth results. Note that this effect is often assumed to be positive and thus has a positive effect on sales. This is the case for a good-quality product. But word-of-mouth can also be negative. This is what happens when buyers discover that the product does not suit them (Kalish, 1983).
In the case of durable goods, i.e. goods for which only one unit is sold to each buyer, there is a saturation effect. Each new sale reduces the future market. As total sales increase, there is less and less unsatisfied demand, which reduces future sales (Bass, 1969; Kalish, 1983).
Network Externalities
For certain products, willingness to pay increases with the installed customer base (the total number of users of this product). This phenomenon is a positive network externality. The concept of network externality means that the value of a product to a user depends on the number of other users of this product. More specifically, the value of joining a network depends on the number of people connected to this network (Economides, 1996). Several studies suggest that network externalities are capable of slowing or accelerating the adoption of a product or even of pushing for the adoption of an inferior-technology product.
A product’s rise in value thanks to its installed base derives from three factors: exchange, stability and extrinsic benefits. First of all, Economides (1996) emphasizes the possible exchange of content or software between users of a network good. This increases the value of the network. Secondly, users prefer goods for which there already exists a significant customer base, as it reflects the long-term stability of the product on the market. This point is all the more important if the product’s use is linked to the presence of other goods. Consumers prefer a good which is more likely to obtain additional benefits when associated with content such as manuals, books, or extensions of qualified staff (Parker and Van Alstyne, 2005). Thirdly, existing consumers form expectations about the future size of a network. This is a fundamental difference with conventional markets. The concept of mindshare is used to describe consumers’ knowledge of a product and to assess future success (Parker and Van Alstyne, 2005). It partly figures the expectations of consumers on the future deployment of a product.
Pricing Policies
Different Types of Pricing
In solving pricing problems, there are three types of optimal price (Jorgensen, 1986): the myopic optimal price, the optimal constant price and the optimal dynamic price. The myopic optimal price maximizes current profit. It is equivalent to the price that maximizes intertemporal profit when the interest rate tends towards infinity (the economic agent has, in this case, an unlimited preference for the present). It is actually the price in the static setting. The optimal constant price is the constant price over the whole sales period that maximizes intertemporal profit. Optimal constant price makes sense when it is not possible for the firm to change its price. The optimal dynamic price maximizes at each moment the intertemporal profit. As such, it takes into account the dynamic effects on future prices. The myopic optimal price is often used as a point of comparison for the optimal dynamic price. The difference between the two prices is explained by the dynamic effects (Seetharaman, 2009).
The Impact of Dynamic Effects on Pricing
In management science, there are two main questions about pricing (Kalish, 1983). The first is to know what the optimal dynamic price level is, relative to the myopic price. The second is to characterize the pattern of optimal dynamic pricing over time. Since data are rarely available publicly, it is difficult to compare an optimal dynamic price to a myopic optimal price. However, the prices over a period of time are observable, in particular for goods sold on the internet. Parsing methods can retrieve the desired information automatically on the Internet, for the creation of databases. It is therefore possible to deduce the form of intertemporal pricing policies (Bass 1969, Mahajan et al 1990, Bass et al. 1994, Rao an Kartono, 2009).
Impact on the Current Price Level
The firm makes a trade-off between current profits and future profits according to its preference for the present (represented by the discount rate). The decreasing slope of the learning curve on costs creates an incentive to lower the current price that maximizes intertemporal profit. This is because a lower price allows to sell (and therefore produce) more today. This lowers future costs and thus increases future profits (Kalish 1983; Seetharaman, 2009).
Similarly, positive word-of-mouth effects create an incentive to offer a price lower than the myopic price. Indeed, a lower price today increases sales, and so the installed base, which increases the product’s diffusion thereafter, and therefore future profits. On the contrary, the saturation effect incites to increase the price. In fact, a higher price implies fewer sales today, which preserves a larger market for the future. This permits better future sales and higher future profits.
Impact on the Form of Intertemporal Pricing
Various factors affect the form of pricing policies (Jorgensen, 1986; Rao an Kartono, 2009). This especially refers to learning effects on costs and scattering effects in demand. The market’s structure also matters. Indeed, a monopoly and a firm in competition (or potential) do not act in the same way. The type of good (sustainable or unsustainable) is another determinant factor. The interest rate, as a measure of the relative importance of current and future profits, influences the form of the pricing policy. The interactions between these various factors create the basis for the various forms of intertemporal pricing policy: skimming, penetration, and the inverted U curve (a succession of the two previous types).
The Forms of Pricing Policies
The Skimming Policy
Skimming is the situation in which prices gradually decline over time. This occurs for a durable goods firm that can commit to prices with costs that decline with experience (Kalish, 1983). This form also appears when the goods are subject to network effects (Economides, 1996). This is because the firm initially charges low in order to subsidize the product’s customer base. The firm then charges more, when the consumers’ willingness to pay increases because of network effects. This policy makes it possible to tap the consumer’s intertemporal surplus (Mahajan et al. 1990). The skimming policy implies an initial price higher than the myopic price.
The Penetration Policy
Penetration policy is about prices that rise over time. It appears especially when the word-of-mouth is positive or when there are network effects. The intuition is that the firm prices the good cheaper when it is just introduced. Thus, a greater number of consumers buy it. This happens when innovators (early adopters) have a strong positive effect on followers (later adopters) A low introductory price encourages (subsidizes) the former to buy the product. Thus, when the product is well established, prices may rise because the followers’ contribution to sales decreases over time (Mahajan, 1990). The penetration policy generates an initial price lower than the myopic price.
Penetration Followed by Skimming
The policy of penetration followed by skimming takes the shape of an inverted U price curve. Prices increase initially and then decrease. This policy appears when the determinants of penetration outweigh those of skimming in the beginning and then the contrary (Kalish, 83; Xie and Sirbu 95). This is particularly true for durable goods that have network externalities, such as computers or software. This is because, early in the life cycle, the positive diffusion effects outweigh the negative saturation effects. At the end of the cycle, it is the opposite. The policies of penetration and of penetration followed by skimming are the most studied in the literature (Mahavan et al. 1990) and the most observed in practice (Krishnan et al. 1999).
The Foundations of Dynamic Pricing
Seminal Models
The first works that incorporated price dynamics were concerned with the existence of an equilibrium and not with the form of pricing policies. Evans (1924) suggests one of the first applications of the calculus of variations to the analysis of an economic problem. It is the first article to characterize monopolistic behavior in a dynamic setting where time tevolves along the interval [0, T]. It uses a quadratic cost function and introduces the dynamics at the level of demand. Demand D depends on price and the evolution of price over time Ï. The variation of any function f with respect to time t, is 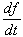 hereinafter written: ƒ . By omitting the temporal arguments in the functions, we obtain
hereinafter written: ƒ . By omitting the temporal arguments in the functions, we obtain 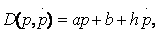 (1)
(1)
where 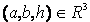 are the model’s parameters.
are the model’s parameters.
The firm’s problem is to maximize profit on [0, T]. T is the time horizon, supposed to be finite and short enough to justify the fixed demand and cost functions and the omission of a discount factor. This calculus-of-variations problem requires the initial price Ï0 and the final price ÏT to be given. These assumptions are quite strong because, in practice, these boundary conditions result of discretionary choices by the firm.
Evans (1924) shows that there is always a unique equilibrium. This result actually generalizes that of the static monopoly for which 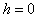 . However, Evans (1924) fails to obtain a general result on the form of an intertemporal pricing policy.
. However, Evans (1924) fails to obtain a general result on the form of an intertemporal pricing policy.
At a time when game theory was yet to be developed, Roos (1925) generalized the previous model to a duopoly. The assumptions on the demand and cost functions are identical.
Tintner (1937) uses Evans’s (1924) monopolistic setting without specifying the demand and cost functions. He works on the analytical properties of general functions. He proposes a demand function that depends on price and on the derivatives of price with respect to time. Tintner (1937) interprets the integration in the demand function of the various derivatives of price as the inclusion of agents’ expectations about future price developments. The demand function (1) becomes:
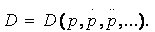
In the specific case of Evans (1924), where demand depends on price and on the first derivative of price 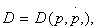 Tintner reaches a simple analytical result that serves as the rule of optimization: at the optimum, the firm always chooses a price such that
Tintner reaches a simple analytical result that serves as the rule of optimization: at the optimum, the firm always chooses a price such that 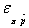 verifies:
verifies:
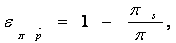
with 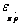 the partial elasticity of profit with respect to price variation rate, Ï€s the static monopoly’s profit the
the partial elasticity of profit with respect to price variation rate, Ï€s the static monopoly’s profit the
dynamic monopoly’s profit. This result is related to that of the static monopoly for which the elasticity of profit with respect to price is zero: . Thus, while the monopolist in a static setting chooses its price so that
the elasticity of profit with respect to price is zero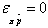 , the dynamic monopolist considers the partial elasticity of profit with respect to price variation. This result clearly illustrates how the inclusion of dynamic effects alters the rules of optimization taken from the static framework.
, the dynamic monopolist considers the partial elasticity of profit with respect to price variation. This result clearly illustrates how the inclusion of dynamic effects alters the rules of optimization taken from the static framework.
In the models we have just discussed, the dynamics are introduced at the level of the demand that now takes into account the different price variations. Such a model makes it possible to apply the calculus-of-variations techniques that address these optimization problems. The issue, in this context, is not to study the form of the pricing policy but to verify the existence and stability of the equilibrium in the market. If the limits of the calculus of variations make it impossible to answer the first question, the answer to this second question is nevertheless possible.
Contemporary Models
Evans’s (1924) and Roos’s (1925) problem was addressed much later by Fershtman and Kamien (1987) who founded the literature on sticky prices. They analyze, in the case of a duopoly, the infinite horizon open-loop Nash equilibrium. Posing 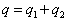 where qi (i= 1,2) is the quantity sold by firm i, the dynamics is given by
where qi (i= 1,2) is the quantity sold by firm i, the dynamics is given by
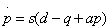
These authors are mainly interested in the relations between the dynamic game’s Nash equilibrium and the static equilibrium (obtained when s→∞ ), and the implications of the various informational structures. Fershtman and Kamien (1987) calculate the equilibrium of the firm in infinite horizon in the case of a duopoly. Dockner and Gaunersdorfer (2001) calculate in finite and infinite horizon the open-loop and closed-loop Nash equilibria for n firms.
The different forms of pricing policy meet. They may be linked to the firms’ desire to discriminate between consumers (skimming policy), a logic of development of the installed base (penetration policy) or to market saturation (inverted-U curve). Attempting to measure these determinants generated many empirical contributions. Bils and Klenow (2004), for example, show the practical importance of sticky prices.
We thus see that the issue of the intertemporal monopoly has been studied since the very beginning of dynamic economics with Evans (1924) and Tintner (1937). Roos (1925) immediately generalized these results to a duopoly. These issues have remained important in economics as evidenced by the work of Fershtman and Kamien (1987, 1990) and Dockner and Gaunersdorfer (2001). Some developments are made to reflect agents’ expectations (Mackowiak and Wiederholt, 2009).
Models of Monopoly
Reservation Prices and Market Size
Bass (1969) and Robinson and Lakhani (1975) hypothesize that the market’s size M is determined at the time the product is introduced and remains unchanged throughout the product’s life cycle (Kalish, 1985). However, from a theoretical standpoint, there is no reason why the population of buyers should remain constant. To the contrary, the modeler may consider a variable population of potential buyers (Mahajan et al., 1990).
In the literature, until the models based on Robinson and Lakhani (1975), the market’s size is constant and price affects sales only through the adoption rate. The potential market size M depends on certain key variables (price, product quality, advertising or consumer wealth). By explicitly linking the total market size M to the price p, the equation describing the evolution of current sales is:
 (2)
(2)
with 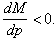
M (p) is interpreted as the total number of consumers whose reservation price exceeds p. The first author to introduce the concept of reservation price in diffusion models is Kalish (1983, 1985). The reservation price w is the maximum amount a consumer is willing to pay for a good. It represents the value of the good to the consumer in monetary terms. Ifw is distributed randomly in the population (Xie and Sirbu, 1995), following a density function z, the potential market is given by
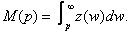
This equation represents the potential dynamic demand. The demand is dynamic because it evolves over time. Its evolution depends on exogenous factors such as time as well as endogenous factors such as past sales. This demand is potential because it is not satisfied instantly. The potential current demand is therefore not equal to current sales. This captures the mechanism of sales smoothing. In practice, when a potential customer has a willingness to pay that is superior to the price of a good, they do not necessarily buy the good immediately. More or less time may elapse before they proceed to their purchase. The number of realized sales increases, however, with the number of individuals whose willingness to pay is higher than the current price and who have not yet made a purchase. It increases with the good’s diffusion rate .This justifies proposing to model the current sales as:

where and g (p) represent respectively the current sales and potential dynamic demand (or dynamic demand).
Numerical Pricing Rules
In the theory of the dynamic monopoly, price is endogenous. It is the result of an optimization process. This is different from the Generalized Bass Model (GBM, Bass et al., 1994), which incorporates the price exogenously. In the GBM, the price does not result from the intertemporal profit’s maximization. Only the impact of price on sales is taken into account. In this sense, in the GBM, the price variable is passive.
Note that, by posing 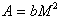 and
and 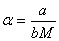 , (2) can be written
, (2) can be written

(3)
where A is the good’s diffusion rate. In (3), the diffusion rate is constant.
The GBM, although it helps to explain the evolution of sales, describes a “passive” firm, in that it does not manipulate any strategic variable in order to maximize its profit. In particular, it determines neither the good’s price nor the level of advertising. Yet these are the basic variables of the firm’s marketing mix (Jorgensen et al., 2007). This shortcoming of the model is overcome by Robinson and Lakhani (1975), who notice that the diffusion rate could be generalized into a function of price, or of the amount of advertising. Representing the price effect on sales is very simple. With the product price p (t), the product’s diffusion rate becomes A = A (p).The equation of the variation in sales (3) is:
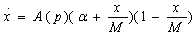 (4)
(4)
Robinson and Lakhani (1975) propose the specification , with k> 0 the price elasticity of demand. Thus, (4) becomes:
. 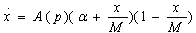 (5)
(5)
A further assumption is that the market cannot be saturated instantly, even with low prices. This assumption captures the effect of the dissemination of sales over time. Besides, dynamics are introduced on the supply side by making the unit production cost c depend on previously produced quantities, as in Arrow (1962).
The problem posed by Robinson and Lakhani (1975) is, choosing price for each time step t, to maximize the intertemporal profit

under the constraint of sales trends (5). This is an optimal control problem.
Robinson and Lakhani (1975) achieve three main results. Firstly, they find a simple pricing rule: pricing policy mimics the diffusion process. Thus, price increases (resp. decreases) when sales increase (resp. decrease). This result, obtained from a numerical simulation was later formally established for more general sales functions by Kalish (1983). Secondly, the optimal dynamic price is always lower than the myopic optimal price (the optimal myopic price corresponds to the static problem’s price). This result is important because observing that a company prices low no longer means that the company has no market power, contrary to the static case. This can for example be the result of a desire to penetrate the market (the price curve is increasing). This result also suggests that the firm’s intertemporal pricing policy benefits the consumer (Jorgensen and Zaccour, 2004). Finally, the authors’ simulations show that the discounted profits are far higher when a pricing policy based on intertemporal optimization is implemented, in comparison with those obtained by an optimization in a static framework. Both consumers and the firm have an interest in a pricing policy designed on the grounds of a dynamic optimization and not of a static optimization.
Note that modeling sales according to (5) can be done under the GBM. The difference is that, in Robinson and Lakhani (1975), the choice of a price leads to intertemporal profit maximization, whereas there is no optimization in the GBM. Robinson and Lakhani (1975) have initiated a important research programme in marketing by generalizing the GBM to study intertemporal pricing (Kalish, 1983, 1985, Jorgensen, 1986; Sribu and Xie, 1995; Dockner et al., 2000).
Formal Pricing Rules
Families of Demand Functions
Kalish (1983) studies a monopoly’s intertemporal pricing policy, by generalizing the previous models and results. He keeps the dynamic effects on the supply side (learning effect) and the demand side (diffusion effects). Kalish (1983) first proposed a current sales function that depends jointly on the current price and on past sales. He then specifies it in various ways. This allows him to properly control the robustness of his results, with respect to the various functional forms. This model generalizes many previous contributions and is the basis for many later developments in monopoly and oligopoly settings (Dockner and Jorgensen, 1988; Xie and Sirbu, 1995; Dockner et al., 2000).
The unit cost or marginal cost c is a function of experience, of which aggregated sales are a proxy. We have 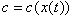 . In addition, according to Jorgensen and Zaccour (2004), learning in terms of production implies
. In addition, according to Jorgensen and Zaccour (2004), learning in terms of production implies 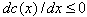 . Current demand (or current sales) is a function of the current price p (t) and of cumulative sales x (t).Thus,
. Current demand (or current sales) is a function of the current price p (t) and of cumulative sales x (t).Thus,
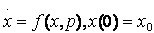 (6)
(6)
It is postulated that an increase of the good’s price reduces current sales . This hypothesis is consistent with the normal character of the good. The effect of the good’s diffusion (past sales) on the current sales, is not uniform: when a “good” product is introduced on the market, the effect will be positive because of the word-of-mouth, which helps potential customers know the quality of the product. On the contrary, in the case of durable goods, the effect is negative. The reason is that each additional sale removes a buyer from the market, which reduces the current demand.
Where the demand function has a general formulation, as in (6), the pricing policy is not easily interpretable. Kalish (1983) therefore specifies the demand function in such a way as to obtain less general but more precise results. By eliminating the diffusion effects, (6) is:
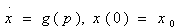
In this case, if the discount rate is not zero, prices decrease over time. The policy implemented is a skimming policy.
With a demand functional in which the price effects and the scattering effects are multiplicatively separable, we have
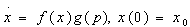
This functional is often used in the literature (Bayus, 1995; Dockner et al. 2000; Chatterjee, 2009). The advantage with this functional form is that it provides relatively precise analytical results, despite having few constraints. Moreover, Jain and Rao (1990) test several functional forms for the current sales. They show that the specifications for which the price effects and diffusion effects are multiplicatively separable have the best explicative power for the data in their possession.
If the learning in terms of production and the discount rate are neglected, the pricing policy mimics the diffusion process. Thus, when 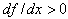 (resp
(resp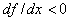 ), prices increase (resp. decrease). Jorgensen and Zaccour (2004) note that for durable goods like electronics, where
), prices increase (resp. decrease). Jorgensen and Zaccour (2004) note that for durable goods like electronics, where 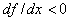 due to the saturation effect, prices effectively decrease over time.The pricing policy is therefore in inverted-U.
due to the saturation effect, prices effectively decrease over time.The pricing policy is therefore in inverted-U.
Note that in cases where there is no diffusion effect on the demand side and only the effect of learning on the supply side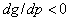 ,
,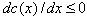 and , prices decrease over time (Kalish, 1983; Zaccour Jorgensen, 2004).The skimming policy is an expected consequence of the decrease of costs with the level of production.
and , prices decrease over time (Kalish, 1983; Zaccour Jorgensen, 2004).The skimming policy is an expected consequence of the decrease of costs with the level of production.
Functional Forms
Price Effect
The simplest form for the demand function g (p) is the linear form:
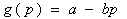
This function is particularly used by Jorgensen and Zaccour (2004).
Another form used for g (p) is the exponential:
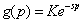
where s is the elasticity of demand.
This form is used in 1975 by Robinson and Lakhani. This is the one most often used nowadays (Dockner and Zaccour, 2004).
The last form is the power function of the type:

where is the price elasticity of demand. Bayus et al. (2000) and Dockner et al. (2000) propose a literature survey of the use of this function.
Network Externalities
In presence of scattering effects or of networks externalities, the function f can be specified as:
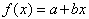
If the good is sustainable, then we must take into account the market’s saturation. In this case, Bass (1969) and Robinson and Lakhani (1975) propose:
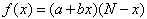
In the latter case, network effects are uniform. A diffusion which is not uniform in regard of network externalities is modeled by:
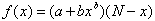
For a presentation and discussion of other functional forms, the reader may consult Jain and Rao (1990) or Bayus (1995). The conclusion of this literature is that in presence of network externalities, the price starts low, until the installed base expands sufficiently. Then, when externalities begin to have an impact, the price gets higher. This implies a penetration pricing policy.
Competition Models
In the static setting, many research works incorporate competition. However, Jorgensen (1986) and Krishnan et al. (1999) note that in the dynamic framework, much of the literature is confined to the monopolistic setting. To authors such as Kalish (1988) and Bayus (1995), it seems that the results for monopolies can be generalized to oligopolistic situations. If true, there is no need to explicitly consider competitive interactions. Other authors like Dockner et al. (2000) argue that if there is no specificity of the oligopolistic setting, vis-Ã -vis the competitive setting, this must be that the model does not take into account all the interactions between the products and/or between the players. Consequently, Krishnan et al. (1999) and Dockner et al. (2000) suggest that future literature should include the effects of competition to establish intertemporal pricing rules. Indeed, the dynamics of competitive interactions are fundamental to understanding the growth of a class of products. The types of products that attract more producers spread faster and the products that spread faster attract more producers. With the exception of Dockner and Jorgensen (1988), who study the case of ncompetitors, most models are duopolistic. These models can explain a wide range of pricing schemes. Chatterjee (2009) and Chan et al. (2009) provide a literature review of the models that include competition. The first author insists on normative models and the second on descriptive models.
Introducing competition changes the behavior of the incumbent firm in several ways. For example, a firm can reduce its product’s diffusion rate to send potential entrants a signal that the market is small. It may also wish to accelerate the diffusion rate in order to achieve a larger installed base, if the good is subject to network externalities. The issue of entry is extensively treated in the literature, and appears to be a subject of consensus (Jorgensen and Zaccour, 2004). The first mover has an advantage in several ways. It enjoys learning opportunities about the technology. It creates a reputation as a leader in this market and can potentially get captive customers if it implements switching-costs. Because of these effects, pioneers have a higher long-term market share than their competitors. The pioneer’s problem is its exposure to risks of failure, and to free-riding from potential entrants, who may enter later but enjoy a technological leap.
The Dynamic Oligopoly
Dockner and Jorgensen (1988), Dockner et al. (2000) and Jorgensen and Zaccour (2004) generalize to oligopolies Kalish’s (1983) dynamic monopoly. Chatterjee (2009) reviews this literature. For an introduction to the techniques of differential games, the reader may refer to Dockner et al. (2000) and Jorgensen et al. (2007). Dockner and Jorgensen (1988) wrote the seminal article on the dynamic oligopoly. We present the various proposed specifications. The authors begin their analysis with a general current demand function:
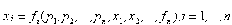 . (7)
. (7)
The general model that incorporates learning effects in production and scattering effects in demand leads to results which are not easily interpretable. Following Kalish (1983), the authors then specify their model to obtain precise analytical results.
Keeping only the effects of sales for its own product and the prices of all the goods that are multiplicatively separable, (7) becomes
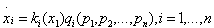 (8)
(8)
In this case, for a zero interest rate, prices increase (resp. decrease) over time when is positive (resp. negative) for any i. Note that a priori is positive in the beginning of the sales cycle and negative at the end. The pricing policy is therefore shaped like an inverted U-shaped curve.
The authors also consider the combined sales for all firms of good x (but not the combined sales for each firm ). (8)becomes:
 (9)
(9)
When the impact of price is linear and the impact of discounting and of learning are neglected, then prices increase (resp. decrease) over time when is positive (resp. negative). Pricing also follows an inverted U curve.
The last case deals with duopoly. Current sales only depend on the price of good $ i $ and on past sales of both goods:
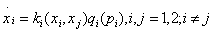
In this case, neglecting the discount rate and the learning in production, prices increase (resp. decrease) over time when  is positive (resp. negative).
is positive (resp. negative).
Finally, the main result derived from these cases is that prices increase at the start of the cycle (imitation effects prevail) and decrease at the end of the cycle (saturation effects are stronger). Thus the pricing policy that emerges is that of the inverted U curve.
The above results are not related to the choice of price as the decision variable for the firms. Rao and Bass (1985) analyze the case where firms in oligopoly sell undifferentiated products. The price is common to all firms, who choose their production level. Isolating different dynamic effects, the results are similar to those of Dockner and Jorgensen (1988).This is because the saturation effect causes prices to decline over time. With positive diffusion effects, prices increase over time.
Strategic Interactions
Regarding supply, network externalities may determine the choice of a technology by a firm. Standards are sometimes imposed by administrative authorities or by a group of firms, but are often the result of a choice made by the dominant firm on this market. When technological choices are imposed by market forces, dominant firms can achieve compatibility by choosing a technology individually, or collectively if it encourages other businesses to adopt the same technology. Firms may also decide not to make their products compatible (Xie and Sirbu, 1995). Until the issue of compatibility between products is resolved within a given industry, consumers tend to delay their adoption of a technological product. The impact of the choice of compatibility with the competition therefore deserves to be studied. The work of Economides (1996) addresses these issues and provides input for the development of diffusion models (Chatterjee et al., 2000).
Some markets are characterized by the compatibility of their product with others. In this case, the utility a consumer derives from a product also depends on the penetration of compatible products (Xie and Sirbu, 1995). Compatibility issues are particularly important in markets for technological goods where standardization permits the joint use of products, minimizing the need for learning how new products work and reducing the uncertainty associated with new technologies. For Tirole (1988), externalities can be direct or indirect. A direct externality occurs when a consumer’s utility increases with the installed base of the same network (e.g. the number of telephones in the same network). Indirect externalities are derived from the installed base of compatible goods. Network externalities have implications in terms of demand and in terms of supply. In terms of demand, network externalities lead to a coordination problem for the consumer, regarding which standard they should choose for the good they want to buy. Thus, consumers may delay the purchase of the property to reduce the uncertainty about its final utility. Policies that reduce this uncertainty, therefore gain in importance. In some cases, however, the marketing of a deliberately non-compliant product can be a signal by the firm that it has the capacity to be the leader on the future market.
Extensions
The research on the monopoly’s dynamic pricing is the foundation of this literature. On this basis, more complex models have been developed, to answer new questions. The relative simplicity of the earlier models had the advantage of leading to analytical results. Studying more complex issues requires accepting results from numerical simulations.
Uncertainty in Demand
Several authors relax the assumption that demand is well known, a simplification that previous models made (Chatterjee, 2009). Demand is estimated before the start of sales. The firm’s learning process is based on the demand effectively materialized in prior periods. This learning enables the firm to establish the price for the current period. While the pricing policy is being implemented, the firm learns about demand in real time. With a series of numerical simulations, Lin (2004) shows that possessing estimates can significantly improve profit, even if the estimates are not always accurate. Bertsimas and Perakis (2006) study the oligopolistic case and argue that the oligopolistic dynamic optimization policy that maximizes the intertemporal profit increases a firm’s expected profit more than other methods would, and this, no matter what pricing policy the other firms pursue.
Demand and Reference Prices
A part of the literature focuses on dynamic pricing when consumer preferences depend on reference points (Seetharaman, 2009). Helson (1964) predicts that consumers consider a particular price by comparing it to a past price that serves as a reference price. Briesch et al. (1997) suggest, according to certain empirical results, that the firm’s past price is the best candidate as the reference price. Based on prospect theory, Popescu and Wu (2007) consider the problem of dynamic pricing of a monopoly when demand is sensitive to the firm’s pricing history. In this framework, consumers have psychological biases in their purchasing decision. When the firm modifies the price for its good, consumers form a reference price that they adapt according to their perceptions on prices. Popescu and Wu (2007) show that in that case, when consumers perceive increases (resp. decreases) in prices, the optimal policy is penetration (resp. skimming).
Multi-product Markets and Two-sided Markets
The issue of multi-product pricing arises naturally after that of single-product pricing. In fact, this generalization would provide a more realistic analytical framework to understand the relationships between products. This would facilitate the production of more robust forecasts; the proposed pricing policies would be more relevant (Bayus et al, 2000; Mahajan et al. 2000; Chatterjee, 2009). Empirical studies are being developed. An example of such studies analyses web browsers and complementary software (Gallaugher and Wang, 2002). However, the formal analysis of dynamic markets with several complementary products remains limited, even though its prescriptions would obviously be of interest to practitioners. Certain theoretical models, such as those of Bayus et al. (2000), incorporate several products, but they remain unsatisfying. Those models, based on the paradigm of dynamic systems, do not take into account a decision variable such as the price offered by the firm.
In a static setting, there are interesting theoretical developments about two-sided markets. A two-sided market is a market “in which one or several platforms enable interactions between end-users, and try to get the two . . . sides “on board” by appropriately charging each side.” (Rochet and Tirole, 2006). The literature on two-sided markets suggests that many markets subject to network externalities are characterized by the presence of two distinct sides. Consumers of a good on a two-sided market do not necessarily consume the complementary good. Examples of two-sided markets include: the video game market, with on one side players and on the other side game publishers; or the newspaper market, with advertisers and readers. The interactions between the two sides of the market induce strong complementarities between the products. Each side has an interest in the other side’s possessing the good in question. This cross-complementarity between products generates externalities. One same firm produces and prices both complementary goods.
Expectations
The major weakness of most dynamic pricing models is that they do not consider consumer expectations (Mahajan et al. 1990; Chatterjee, 2009). This is especially true for models based on diffusion processes, where introducing expectations would complicate too much the analysis to provide analytical results (Xie and Sirbu, 1995; Dockner et al., 2000). In their purchase decisions, buyers are only sensitive to the current state of the relevant variables, i.e. current price and past sales. In their decision, they do not anticipate price changes. But these expectations are likely to change the models’ results, e.g. for what concerns price discrimination policies.
Actually, certain studies do take into account rational expectations (Jorgensen and Zaccour, 2004; Chatterjee, 2009). This is particularly true of Chatterjee et al. (2000). Chan et al. (2009) offer a synthesis of this literature. In those models, pricing policies are sometimes characterized by using analytical methods, but more often by numerical simulations – this shows that incorporating expectations leads to problems too complex to permit analytical results. Taking into account expectations reduces both the price and the slope of the intertemporal pricing policy, but the qualitative results are not fundamentally different.
By the way, even without expectations, the models explain well the observed data (Bass et al. 1994, Krishnan et al. 1999, Bass 2004). They have been applied successfully to technological goods such as mobile phones, satellite TV and Internet access (Bass, 2004), to the diffusion of various categories of related products (Van den Bulte, 2000) and to diffusion in an international context (Talukdar et al., 2002).
Microfoundations
The diffusion models postulate certain relationships between variables at an aggregated level (Mahajan et al. 1990; Chatterjee, 2009). A classical variable of interest is the level of sales at a particular date. The analysis is done at a macro-economic level and not a micro-economic level (Chatterjee et al., 2000). This approach facilitates the analysis but poses the problem of its foundations in terms of individual behavior. There is still the question of whether diffusion models may be built by aggregating the demands of consumers who maximize their utility function. Since personal characteristics (income, preferences, attitude towards risk) can vary, all individuals do not have the same probability of buying the good at the same time (Mahajan et al., 1990).
If there is a literature on the aggregation of individual demands, it is not very developed (Roberts and Lattin, 2000). Note, in particular, the works of Roberts and Urban (1988), who postulate that people maximize a specific utility function. Their basic assumption is that an idiosyncratic probability of purchase is assigned to each individual. Thus, the diffusion rate is specific to each consumer. The major problem with this approach of individual utility maximization is that the solutions to the problems are very difficult to calculate (Chatterjee et al., 2000), even in a static setting (Roberts and Lattin, 2000).
Conclusion
This literature review is about dynamic pricing. Dynamic pricing is based on dynamic economics, new product diffusion, and game theory. Our review confirms that the issue of dynamic pricing is essential, it has applications in a wide range of situations and it has alimented numerous research works since the 1920s. Having presented the seminal works on the topic, we have shown how the analyses were constructed in cases of monopolies and oligopolies.
The literature on dynamic pricing could further develop in different directions. Firstly, certain aspects of the agents’ psyche could be incorporated into the models. Then it could be interesting to provide an individual-scale foundation to the relationships modeled at an aggregated scale. Moreover, it would be interesting to integrate uncertainty more explicitly, for the models to become more realistic. Finally, incorporating expectations is likely to enrich the analysis. These avenues of research, although already initiated, are still in their infancy. This illustrates the intrinsic difficulty of the issue of dynamic pricing.
References
Arrow, K. J. (1962). “The Economic Implications of Learning by Doing,” Review of Economic Studies, 29 (3). 155-173.
Publisher – Google Scholar
Bass, F. M. (1969). “A New Product Growth Model for Consumer Durables,” Management Science, 15 (4). 215-227.
Publisher – Google Scholar
Bass, F. M. (2004). “Comments on ‘A New Product Growth Model for Consumer Durables,’ The Bass Model,”Management Science, 50 (12). Ten Most Influential Titles of Management, 1833-1840.
Publisher – Google Scholar
Bass, F. M., Krishnan, T. V. & Jain, D. C. (1994). “Why the Bass Model Fits Without Decision Variables,” Marketing Science, 13 (1). pp.203-223.
Publisher – Google Scholar – British Library Direct
Bayus, B., Kim, N. & Schoker, A. (2000). “Growth Models for Multiproduct Interactions: Current Status and New Directions,” New-Product Diffusion Models, eds. V. Mahajan, E. Muller, Y. Wind, Boston, MA, Kluwer, 141-164.
Publisher – Google Scholar
Bayus, B. L. (1995). “Optimal Dynamic Policies for Product and Process Innovation,” Journal of Operations Management, 12 (4). 173-185.
Publisher – Google Scholar
Bertismas, D. & Perakis, G. (2006). Dynamic Pricing: A Learning Approach, Mathematical and Computational Models for Congestion Charging, eds. S. Lawphongpanich, D. Hearn, M. Smith, Springer U.S.
Publisher – Google Scholar – British Library Direct
Bils, M. & Klenow, P. J. (2004). “Some Evidence on the Importance of Sticky Prices,” The Journal of Political Economy, 112 (7). 947-985.
Publisher – Google Scholar – British Library Direct
Briesch, R. A , Krishnamurthi, L. , Mazundar, T. & Raj, S. P. (1997). “A Comparative Analysis of Reference Price Models,” The Journal of Consumer Research, 24 (6). 202-214.
Publisher – Google Scholar – British Library Direct
Chan, T., Kadiyala, V. & Xiao, P. (2009). “Structural Models of Pricing,” Handbook of Pricing Research in Marketing, ed. V. Rao, EE.
Publisher – Google Scholar
Chatterjee, R. (2009). “Strategic Pricing of New Product and Services,” Handbook of Pricing Research in Marketing, ed. V. Rao, EE.
Publisher
Chatterjee, R., Eliashberg, J. & Rao, V. (2000). “Dynamic Models Incorporating Competition,” New-Product Diffusion Models, eds. V. Mahajan, E. Muller, Y. Wind, Boston, MA, Kluwer, 165-206.
Publisher – Google Scholar
Dockner, E. & Jorgensen, S. (1988). “Optimal Pricing Strategies for New Products in Dynamic Oligopolies,” Marketing Science, 7 (8). 315-334.
Publisher – Google Scholar
Dockner, E., Jorgensen, S., Long, N. & Sorger, G. (2000). Differential Games in Economics and Management Science, Cambridge University Press.
Publisher – Google Scholar
Dockner, E. J. & Gaunersdorfer, A. (2001). “On the Profitability of Horizontal Mergers in Industries with Dynamic Competition,” Japan and the World Economy, 13, 195-216.
Publisher – Google Scholar
Economides, N. (1996). “The Economics of Networks,” International Journal of Industrial Organization, 14 (2). 673-699.
Publisher – Google Scholar – British Library Direct
Evans, G. C. (1924). “The Dynamics of Monopoly,” The American Mathematical Monthly, 31 (4). 77-83.
Publisher – Google Scholar
Fershtma, C. & Kamien, M. I. (1987). “Dynamic Duopolistic Competition with Sticky Prices,” Econometrica, 55 (5). 1151-1164.
Publisher – Google Scholar
Gallaugher, J. M. & Wang, Y.-M. (2002). “Understanding Network Effects in Software Markets: Evidence from Web Server Pricing,” MIS Quarterly, 26 (3). 303-327
Publisher – Google Scholar – British Library Direct
Helson, H. (1964). Adapation-Level Theory, Harper and Row, New York.
Publisher – Google Scholar
Jain, D. C. & Rao, R. C. (1990). “Effects of Price on the Demand for Durables: Modeling, Estimation, and Findings,”Journal of Business and Economic Statistics, 8 (2). 163-170.
Publisher
Jorgensen, S. (1986). “Optimal Dynamic Pricing in an Oligopolistic Market: A Survey,” Dynamic Games and Applications in Economics, ed. T. Basar, Springer Lecture Notes in Economics and Mathematical Systems, 265, 179-237.
Google Scholar
Jorgensen, S., Quincampoix, M. & Vincent, T. L. (2007). Advances in Dynamic Game Theory, Springer.
Publisher – Google Scholar
Jorgensen, S. & Zaccour, G. (2004). Differential Games in Marketing, Kluwer.
Publisher – Google Scholar
Kalish, S. (1983). “Monopolist Pricing with Dynamic Demand and Production Cost,” Marketing Science, 2 (6). 135-159.
Publisher – Google Scholar
Kalish, S. (1985). “A New Product Adoption Model with Price, Adverstising, and Uncertainty,” Management Science, 31 (5). 1569-1585.
Publisher – Google Scholar
Kalish, S. (1988). “Pricing new Products from Birth to Decline: An Expository Review,” Issues in Pricing, ed. T. Devinney, Lexington Books.
Google Scholar
Krishnan, T. V., Bass, F. M. & Jain, D. C. (1999). “Optimal Pricing Strategy for New Products,” Management Science, 45 (12). 1650-1663.
Publisher – Google Scholar – British Library Direct
Lin, P. (2004). “Process and Product R&D by a Multiproduct Monopolist,” Oxford Economic Papers, 56 (4). 735-743.
Publisher – Google Scholar – British Library Direct
Mackowiak, B. & Wiederholt, M. (2009). “Optimal Sticky Prices under Rational Inattention,” American Economic Review, 99 (7). 769-803.
Publisher – Google Scholar
Mahajan, V., Muller, E. & Bass, F. M. (1990). “New Product Diffusion Models in Marketing: A Review and Directions for Research,” The Journal of Marketing, 54 (8). 1-26.
Publisher – Google Scholar
Mahajan, V., Muller, E. & Wind, Y. (2000). “New-Product Diffusion Models: From Theory to Practice,” New Product Diffusion Models, eds. V. Mahajan, E. Muller, Y. Wind, Kluwer, Boston, MA.
Google Scholar
Parker, G. G. & Van Alstyne, M. W. (2005). “Two-Sided Network Effects: A Theory of Information Product Design,”Management Science, 51 (6). 1494-1504.
Publisher – Google Scholar – British Library Direct
Popescu, I. & Wu, Y. (2007). “Dynamic Pricing Strategies with Reference Effects,” Operations Research, 55 (7). 413-429.
Publisher – Google Scholar – British Library Direct
Rao, V. & Bass, F. (1985). “Competition, Strategy, and Prices Dynamics: A Theorical and Empirical Investigation,”Journal of Marketing Research, 22 (3). 283-296.
Publisher
Rao, V. R. & Kartano, B. (2009). “Pricing Objectives and Strategies: A Cross-Country Survey,” Handbook of Pricing Research in Marketing, ed. V. Rao, EE.
Publisher – Google Scholar
Roberts, J. H. & Lattin, J. M. (2000). “Disaggregate-Level Diffusion Models,” New-Product Diffusion Models, eds. V. Mahajan, E. Muller, Y. Wind, Boston, MA, Kluwer, 141-164.
Publisher – Google Scholar
Roberts, J. H. & Urban, G. L. (1988). “Modeling Multi Attribute Utility, Risk and Belief Dynamics for New Consumer Durable Brand Choice,” Management Science, 34 (6). 167-185.
Publisher – Google Scholar
Robinson, B. & Lakhani, C. (1975). “Dynamic Price Models for New Product Planning,” Management Science, 21 (2). 1113-1122.
Publisher – Google Scholar
Rochet, J.-C. & Tirole, J. (2006). “Two-Sided Markets: A Progress Report,” The RAND Journal of Economics, 35 (7). 645-667.
Publisher – Google Scholar – British Library Direct
Roos, C. F. (1925). “A Mathematical Theory of Competition,” American Journal of Mathematics, 47 (8). 163-175.
Publisher – Google Scholar
Seetharaman, P. B. S. (2009). “Dynamic Pricing,” in Handbook of Pricing Research in Marketing, ed. V. Rao, EE.
Publisher – Google Scholar
Talukdar, D., Shudhir, K. & Ainslie, A. (2002). “Investigating New Product Difusion Across Products and Countries,”Marketing Science, 21 (5). 97-114.
Publisher – Google Scholar – British Library Direct
Tintner, G. (1937). “Monopoly over Time,” Econometrica, 5 (1). 160-170.
Publisher – Google Scholar
Tirole, J. (1988). The Theory of Industrial Organization, The MIT Press.
Google Scholar
Van den Bulte, C. (2000). “New Product Diffusion Acceleration: Measurement and Analysis,” Marketing Science, 19 (6). 366-380.
Publisher – Google Scholar – British Library Direct
Winer, R. (2005). Pricing, Marketing Science Institute, Cambridge.
Xie, J. & Sirbu, M. (1995). “Price Competition and Compatibility in the Presence of Positive Demand Externalities,”Management Science, 41 (7). 909-926.
Publisher – Google Scholar – British Library Direc


