An Industrial Organization Approach to the Study of Export Intensity: Strategic Market Interactions and Export Intensity

Introduction

In an increasingly competitive global economy, the internationalization of firms is a potentially difficult undertaking that is likely to preoccupy globally-oriented managers and domestic policymakers alike. This is particularly so for developing economies where export-orientation may be imperative due to relatively small domestic markets, among other factors, that constrain the growth opportunities of local firms (Luo and Tung, 2007). In this context, the crafting of export-promotion strategies and policies is a critical task. However, without a solid understanding of the determinants of export performance, managers and domestic policymakers may not be in a position to confidently, and effectively develop export-promotion strategies and policies, respectively.

Starting with the seminal work of Johanson and Vahlne (1977), the long-standing work of IB scholars on exporting at the firm-level, has the potential to contribute to the design of export-promotion strategies and policies.  Among the various research endeavors in the IB field, much intellectual energy has been devoted to the firm-level export performance research agenda. This research agenda is an empirically-oriented one, with a notable long-standing focus on the relationship between firm-size and export intensity, as measured by the ratio of foreign sales to total sales.

The conventional wisdom is that there is a positive relationship between firm-size and export intensity. While some empirical studies appear to provide evidence in support of this expected positive relationship (Majocchi et al, 2005; Moini, 1995; Wagner, 1995), others suggest that a systematic relationship does not exist (Bonaccorsi, 1992; Pla-Barber and Alegre, 2007). There is even evidence that a negative relationship may exist between firm-size and export intensity (Patibandla, 1995). Thus, on one of the most long-standing issues in the IB field, the empirical export performance literature has failed to yield conclusive results that provide a clear direction for managers and policymakers faced with the challenge of designing export-promotion strategies and policies, respectively.

While the theoretical shortcomings of the empirical export performance literature have been generally acknowledged (Katsikeas et al, 2000; Sousa, 2004), there is virtually no well-articulated direction on a theoretical approach that has the potential to not only yield consistent results on the firm size-export intensity relationship in particular, but also engender greater confidence in the IB empirical export performance research agenda in general. This paper makes a first-step in the direction of the latter.

The articulation of rigorous theoretical arguments in support of empirical propositions constitutes a basic, yet important effort that may engender greater confidence in the IB empirical export performance research agenda. The merit of an IO-based approach is demonstrated in the context of the conventional use of industry-dummy variables to control for “industry effects” when estimating the marginal effect of firm-size on export intensity (Bonaccorsi, 1992; Majocchi et al, 2005; Pla-Barber and Alegre, 2007; Wagner, 2001). Under the IO-based theoretical framework developed in this paper, it is shown that the strategic interaction between firms, together with cross-national differences in consumers’ willing-to-pay, may account for differences in export intensity across firms. This key analytical result provides insights into the stylized “industry effects” phenomenon, and strengthens the theoretical argument in support of the common use of industry-dummies in empirical export performance studies.

The remainder of this paper is organized as follows.  Section two derives the optimal quantities of domestic and foreign sales and the corresponding prices, as well as export intensity, under a discriminating monopolist model of exporting. Section three extends this discriminating monopolist model of exporting by considering a model of exporting under a (symmetric linear) Stackleberg duopoly with price discrimination. Section four discusses the key analytical results. Section five summarizes and concludes.
 
Monopoly with Price Discrimination and Export Intensity

In this section, I derive the analytical results of the conventional model of the exporting firm as a discriminating monopolist across its home- and foreign-market (Hirsch and Adar, 1974). In addition, I define and compute its export intensity.

Consider a single firm that produces a homogeneous product at a constant marginal cost c>0; that is, the cost function is linear in output.¹ Alternatively, the constant marginal cost assumption means that the firm employs a constant return to scale technology. The firm sells quantities q_L and q_F  to a local and a foreign market, respectively. The unit prices of the product in the local and foreign market are given by the linear (inverse) demand curves,p_L(q_L)=a-bq_L, and p_F(q_F)=a-bq_F, respectively. In addition, it is assumed that the foreign market is perfectly competitive, and the monopolist faces the entire downward sloping demand curve in the local market. It is further assumed that the firm can effectively prevent the resale of the product among customers in the local and foreign market; alternatively, there exists transaction costs (e.g., shipping and communication costs) that make it unprofitable for individual customers to engage in the secondary trading of the product between the local and foreign market.

The profit function of the monopolist is given by:

      (1) Ï€_m= (a-bq_L)q_L+(a-bq_F)q_F-cQ      (1)

Where  is the total quantity sold in both the local and foreign market. Let EI^m=q^m_F/(q^m_L+q^m_F) denote the equilibrium export intensity of the discriminating monopolist at the optimal quantities q^m_L and q^m_F. 

The analytical results under a monopoly with price discrimination are summarized in the following proposition:

Proposition 1     If price discrimination is permitted under a monopoly with two groups of consumers, local (L) and foreign (F); then for a>c>0, the equilibrium pairs of quantities and prices for the local and foreign markets, and the export intensity are respectively:  

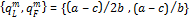
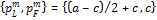
The proof of proposition 1 follows from a straightforward optimization of the profit function in (1) with respect to q_L and q_F. Since the profit function is concave in q_L, the optimal output q^m_L is the solution to the first-order condition ∂π^m/ âˆ‚q_L=0 ⇔ MR_L– MC=0, where MR_L and MC denote the marginal revenue in the foreign market and the common marginal cost, respectively; and the perfect competition optimal quantity q^m_F  is the solution to p_F-MC = 0. In equilibrium, the condition  holds. Once the equilibrium quantities, q^m_L and q^m_F, are obtained, the computation of export intensity is a trivial exercise for the reader.                                                  

From proposition 1, price discrimination is achieved; that is, q^m_L<q^m_F, and q^m_L>q^m_F . At an export intensity of two-thirds, the discriminating monopolist is an exporting firm that sells two-thirds of its total output abroad.

Stackleberg Duopoly with Price Discrimination and Export Intensity

In this section, I extend the discriminating monopolist model of exporting by considering a special case of Kutlu’s (2009) Stackleberg model of competition with price discrimination (Kutlu, 2009).² Under this Stackleberg duopoly model, firm 1 behaves like the Stackleberg leader, while firm 2 operates as the Stackleberg follower. However, both firms produce a homogeneous product at the same marginal cost c>0. This cost-symmetry assumption suggests that both firms employ the same constant returns to scale technology; therefore, differences in firm-size, or technological capabilities are not potential determinants of export intensity under this theoretical framework.

Similar to the setup under the monopoly model with price discrimination in the previous section, I assume that there are two groups of consumers, local (L) and foreign (F), who populate a local and a foreign market, respectively. As before, individual consumers across these markets are assumed to face transaction costs that make it unprofitable for them to resell the product across markets after initial purchases; thus, price discrimination is also permissible in this setting. When ordered by their reservation prices, it is further assumed that the local market comprises a bin of consumers (“high-valued consumers”) with a uniformly higher range of valuations for the product relative to the bin of consumers in the foreign market (“low-valued consumers”).

It is assumed that the linear (inverse) demand curves for the local and foreign markets are respectively:

     (2) P_L= a – b(q¹_L +  q²_L)

     (3)  P_F= a – b(q¹_L +  q²_L+ q¹_F+ q²_F)

Where P_L and P_F are the unit prices of the product in the local and foreign market, respectively; and q^j_L and q^j_F denote the quantities sold by firm j∈{1,2} in the local and foreign market, respectively. Finally, it is assumed that each consumer within each group buys at most one unit of the product.

The results under a Stackleberg duopoly with price discrimination are summarized in the following proposition:

Proposition 2     If price discrimination is permitted in a (symmetric linear) Stackleberg duopoly with two groups of consumers, local (L) and foreign (F); then for a>c>0, the pairs of equilibrium quantities, prices and export intensities for the Stackleberg leader (“firm 1”) and the Stackleberg follower (“firm 2”) are respectively:

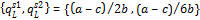
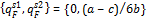
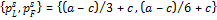
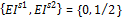
The proof of proposition 2 is provided in the appendix.

Discussion

In Kutlu’s (2009) version of Stackleberg duopoly with price discrimination, we have the general case involving k groups of consumers ordered in bins according to their reservation prices; proposition 2 above constitutes a special case when Therefore, the analytical results of Kutlu (2009) also obtain in proposition 2; that is, the Stackleberg leader supplies the product only to the local market, while the Stackleberg follower supplies the product to both markets. According to proposition 2, the Stackleberg leader supplies the monopoly-output to the local market, while the Stackleberg follower sells one-half of its total output to the foreign market. This implies that the Stackleberg leader targets the high-valued local consumers, while the Stackleberg follower equally serves both the high- and low-valued group of consumers at home and abroad, respectively. At the same time, when the sales decisions of the Stackleberg leader and follower are taken together, price discrimination is effectively obtained; that is,  p^S_L>p^S_F.

Finally, in comparing the analytical results of exporting under a monopoly and a Stackleberg duopoly with price discrimination, an interesting inference can be drawn: the characterization of the competitive structure has implications for the export orientation of firms in a given market or industry. Importantly, the analytical results under a Stackleberg duopoly with price discrimination are essentially induced by the interdependency in the output choices of the two firms engaged in a strategic game. Unlike the Stackleberg leader and follower, the discriminating monopolist is not engaged in such a strategic game. In the absence of strategic considerations, the discriminating monopolist has a higher export intensity than the Stackleberg follower; that is, EI^m = 2/3> EI^S2 = 1/2. In practice, a discriminating monopolist and a Stackleberg follower may be any two firms that operate in two different industries. Thus, what may be captured as an “industry effect” on export intensity in a cross-sectional study of these firms, may very well reflect fundamental differences in the strategic market interaction across industries.
 
Conclusion

This paper demonstrates a potentially fruitful avenue through which the IO field may address the theoretical void that appears to limit the contribution of the IB empirical export performance literature towards the development of coherent export-promotion strategies and policies. It does so by presenting an IO-based framework that sheds light on the stylized “industry effects” phenomenon, and offers a formal justification for the common use of industry-dummies in empirical export performance studies. Under this IO-based framework, it is shown that the strategic interaction between firms, combined with cross-national differences in consumers’ willing-to-pay, may lead to differences in the optimal ratio of foreign sales to total sales across firms. This key analytical result is independent of the scale of operation (i.e. firm size). Finally, it suggests that the underlying competitive structure of a particular market or industry should be subject to more detailed analysis than is currently the case in the extant export performance literature. For this reason, the IO field has a potentially significant contribution to make in this line of research.
 
Acknowledgement

I would like to thank an anonymous referee for providing constructive comments and corrections, and Sharlene Morgan for proof-reading the earlier drafts of this paper. All remaining errors are mine.
 
References

Bonaccorsi, A. (1992). “On the Relationship between Firm Size and Export Intensity,” Journal of International Business Studies, 23(4), 605-635.
Publisher – Google Scholar – British Library Direct

Hazledine, T. (2006). “Price Discrimination in Cournot-Nash Oligopoly,” Economic Letters, 93(3), 413-420.
Publisher – Google Scholar 

Heywood, J. S. & Mcginty, M. (2007a). “Convex Costs and the Merger Paradox Revisited,” Economic Enquiry 45(2), 342-349.
Publisher – Google Scholar – British Library Direct

Heywood, J. S. & Mcginty, M. (2007b). ‘Leading and Merging: Convex Costs, Stackleberg, and the Merger Paradox,’Economics Bulletin 12(12), 1-7.

Hirsch, S. & Adar, A. (1974). “Firm Size and Export Performance,” World Development, 2(7), 41-46.
Publisher – Google Scholar 

Johanson, J. & Vahlne, J. (1977). “The Internationalization Process of the Firm: A Model of Knowledge Development and Increasing Foreign Commitments,” Journal of International Business Studies, 8(1), 23-32.
Publisher – Google Scholar 

Katsikeas, C. S., Leonidou, L. C. & Morgan, N. A. (2000). “Firm-Level Export Performance Assessment: Review, Evaluation and Development,” Journal of the Academy of Marketing Science, 28(4), 493-511.
Publisher – Google Scholar – British Library Direct

Kutlu, L. (2009). “Price Discrimination in Stackleberg Competition,” Journal of Industrial Economics, 57(2), 364.
Publisher – Google Scholar 

Luo, Y. & Tung, R. L. (2007). “International Expansion of Emerging Market Enterprises: A Springboard Perspective,”Journal of International Business Studies, 38(4), 481-498.
Publisher – Google Scholar – British Library Direct

Majocchi, A., Bacchiocchi, E. & Mayrhofer, U. (2005). “Firm Size, Business Experience and Export Intensity in Smes: A Longitudinal Approach to Complex Relationships,” International Business Review, 14(6), 719-738.
Publisher – Google Scholar 

Moini, A. H. (1995). “An Inquiry into Successful Exporting: An Empirical Investigation Using a Three-Stage Model,”Journal of Small Business Management, 33(3), 9-25.
Publisher – Google Scholar

Patibandla, M. (1995). “Firm Size and Export Behavior: An Indian Case Study,” Journal of Development Studies, 31(6), 868-882.
Publisher – Google Scholar – British Library Direct

Perry, M. K. & Porter, R. H. (1985). “Oligopoly and the Incentive for Horizontal Merger,” American Economic Review75(1), 219-227.
Publisher – Google Scholar 

Pla-Barber, J. & Alegre, J. (2007). “Analysing the Link between Export, Innovation and Size in a Science Based Industry,” International Business Review, 16(3), 275-293.
Publisher – Google Scholar 

Salant, S. W., Switzer, S. & Reynolds, R. J. (1983). “Losses from Horizontal Mergers: The Effects of an Exogenous Change in Industry Structure on Cournot-Nash Equilibrium,” Quarterly Journal of Economics 98(2), 185-199.
Publisher – Google Scholar 

Sousa, C. M. P. (2004). “Export Performance Measurement: An Evaluation of the Empirical Research in the Literature,”Academy of Marketing Science Review, 2004(9). Accessed 4 December 2010. Available:http://amsreview.org/articles/sousa09-2004.pdf.
Publisher 

Wagner, J. (1995). “Exports, Firm Size, and Firm Dynamics,” Small Business Economics, 7(1), 29-39.

Publisher – Google Scholar – British Library Direct

Appendix

For a Stackleberg duopoly with price discrimination, we have a two-period, follower-leader strategic game involving firm 1, and firm 2 as the leader and follower, respectively. At time t=1, firm 1 optimally chooses q¹_L and q¹_F based on the output decision rules it expects the follower to apply in period t=2. In the second period, t=2, the output choices of firm 1 become known to firm 2, which then chooses q²_L and q²_F in accordance with the output decision rules that firm 1 had expected. In game theoretic terms, “backwards” induction is used to obtain the Subgame Perfect Nash Equilibriumas the solution to this leader-follower strategic game; that is, taking the output choices of the leader as given, the follower’s optimal output decision rules are determined at t=2. The leader’s optimal output choices are then determined based on the optimal decision rules of the follower.

At t=2 given the linear demand functions in (2) and (3), and the linear cost function, c(q^j_i) = cq^j_i for i∈{L,F} and j∈{1,2} the profit function of firm 2 is given by:

                (4) 

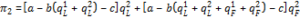
Since Ï€₂ is concave in q²_L and q²_F, the maxima for q²_L and q²_F are given by the first-order conditions ∂π₂/∂q²_L= 0 and ∂π₂/∂q²_F = 0, respectively. Straightforward calculations yield:

for  i∈{L,F}                              (5)

Since ∂π₂/∂q²_F= 0  for i∈{L,F}, it follows that:

   (6) 

Solving (6) for q²_L yields:

   (7) 

Substituting (7) into (5) for i =F , and solving for q²_F yields:

  (8)

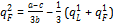
At t=1: I now solve the profit maximization problem of firm 1 subject to firm 2’s optimal decision rules in (7) and (8). The profit function of firm 1 is given by:

                (9)

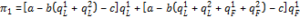
To setup the optimization problem for firm 1, substitute (7) and (8) into (9) to get the following profit function:

    (10)

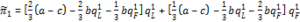
Since the profit function in (10) is concave in q¹_L and q¹_F, the maxima for q¹_L and q¹_F are given by the first-order conditions  and , respectively. Straightforward calculations yield the following equilibrium quantities for firm 1:

   (11)

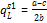
    (12)

To obtain the equilibrium quantities for firm 2, substitute (11) and (12) into (7) and (8) to get:

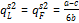(13)

To obtain the equilibrium prices,  and , plug the relevant equilibrium quantities into (2) and (3) to get:

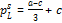  (14)

(15)

The equilibrium export intensity for firm  is defined by:

   (16)

Substitute the equilibrium quantities for firm 1 and firm 2 into (16) to get:

  (17)