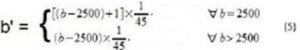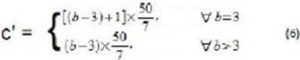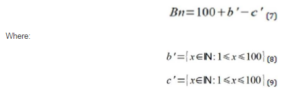Introduction
The competency-based selection problem has already been treated by many authors like Hachicha (2010), Wang (2009), Gilan (2011), Huanga (2005), and Lappas (2009) and approached under many perspectives. For example, in the business context, it can be related to human resource allocation to a specific project or to the composition of an enterprise’s staff.
According to Seol and Sarkins (2006), the quality of the internal auditors is very important and must be in agreement with auditing standards. One fundamental factor in auditing standards is the competence of the internal auditors. The competence of the internal auditors has strong impact on the internal auditing.
The existence of competent auditors in an auditing team is mandatory. This is adopted in every auditing standard. For example, the norm S4 from Information Systems Audit and Control Association (2004) establishes that an information system auditor must be competent, having the skills and knowledge required to conduct the auditing tasks. The information system auditor must have both continuous training and education. So, the competence of auditors is a key factor during auditors’ selection.
The Institute of Internal Auditors of Australia (2010) have published a framework of competences with the aim to “enable the internal audit activity to meet the demands of the future as expectations on the profession grow as part of best practice corporate governance”, reinforcing the importance of question.
Competence is a principle from the Auditors’ Code. The Auditors’ Code establishes that an auditor acts according to his professional abilities. Such abilities emerge from his qualification, training and practice (Pickett, 2010). Competence involves know how and acting in the responsible way, that implies to mobilize, integrate, transfer knowledge, resources and competences, generating economic value to organizations and social value for the individual (Fleury, 2001). Competence encompasses three aspects: knowledge, skills and attitude. Thus, it can be seen as an individual resource stock (Fleury, 2001).
An example of competence is that one required for being an aviator. Suppose that in order to be an aviator, the person must have three skills: knowledge about aircraft instruments operation, skill to operate an aircraft and, the human capacity to perform the task.
Some kinds of competences are indispensable to perform an auditing. For example, suppose that we will perform an auditing in a building under construction. In this case, we will certainly need auditors with civil and electrician engineering degree, project management skills and other skills. The selection of these auditors seems to be easy; however, we may have auditors in the group possessing more than one competence. In a specific selection, embracing auditors with more than one competence, the complexity grows. Besides, the decision making process it is not limited to the selection of auditors that individually concentrate competences. The best selection must be a group of auditors, in which each auditor possesses the greater number of different competences at minimum cost. Figure 1 depicts the complexity of the decision making process.
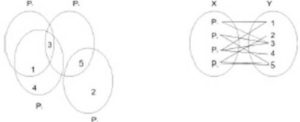
Fig 1. Auditors and their Respective Competences Set
Suppose a competence set Y = {1, 2, 3, 4, 5} and auditors set X = {P1, P2, P3, P4}. Each auditor Pi has his own competences inside the set Y. Suppose that competences of person P1 = {1, 3}, P2={3,5}, P3={1,3,4} and P4={2,5}. Consider now that we will perform an auditing in which the competence 3 is indispensable.. In this case, we can choose one person among P1, P2 and P3 to be part of team. However, each person has a second important characteristic: the cost, in other words, the auditor’s salary. In the context of our problem we need to regard the cost maximum limit. So, we desire to select persons with minimum of costs too. In other hand, we need also persons which the most of number of competences to perform the auditing. In this way, we must regard the costs and the competences of each auditor.
Consider now the auditors set X = {P1, P2, P3, P4}, each one with his own competences as shown in picture 1. As from this set, suppose that we need to create an auditing team and the cost limit is equal to 10000. The following ordered pairs that relate auditors and salary as X’ = {(P1, 2500), (P2, 3000), (P3, 3000), (P4, 4000)}. Let us consider that competences 1, 3, 5 are indispensable. Thus, we can have following teams: T1 = {P1, P2, P3, P4}, T2 = {P2, P3, P4}, T3 = {P1, P3, P4}, T4 = {P3, P4}, T5 = {P1, P2}, T6 = {P2, P4}, T7 = {P1, P3}. Each team has the costs T1 = (2500+3000+3000+4000) = 12500; T2 = (3000 + 3000 + 4000) = 10000; T3 = (2500, 3000, 4000) = 9500; T4 = (3000+4000) = 7000, T5 = (2500+3000) = 5500, T6 = (3000+4000) = 7000, T7 = (2500+3000) = 5500. As we see, if we want to minimize costs and satisfy indispensable competences condition, the best team formation is both T5, T7, with competences T5 = {1,3,5} and T7 = {1,2,3,5}. In other hand, if we want also to maximize competences and regard auditing cost limit, the best solution is T4 = {1,2,3,4,5} that costs 7000, because it concentrates the greatest quantity of competences and it obeys the maximum cost constraint.
Besides the constraints shown previously, there is a dependency relationship among competences. In this work, the dependence among competences means that a certain competence requires another competence so that one solution is viable just when all competences required are part of solution. If we consider that competence 1 depends on competence 2, it means that the solution must have competences 1 and 2; otherwise, the solution is infeasible. Suppose yet that competence 2 requires 7 and 7 requires n, where n is a given competence. In this case, the problem complexity grows, because the algorithm tracks all dependencies and certifies these competences are part of the solution.
As discussed previously, the auditors’ selection process is not a trivial task. In order to support this decision making process, we propose the use of genetic algorithms to maximize competences, considering the indispensable competences, dependency among competences, as well as the cost limitations, ie, the auditing budget. We propose an original evolutionary algorithm to select best team, respecting the budget boundary and indispensable competences.
This paper is structured as follow: Related papers about affair; Genetic algorithms — depicts an overview of genetic algorithms; Genetic Algorithm developed — explain the genetic algorithm developed to solve competence allocation problem; The study — present the scenario studied, how we treated the problem; Tests performed — describes the test cases; Results Reached— bring outcomes reached after applying genetic algorithm and discuss results; Conclusion.
Related Works
The competence selection problem has been approached in literature by many authors. Golec and Kahya (2007) presented a top-down and hierarchical fuzzy model for employee evaluation and selection, obtaining a measurable competences model. Their model was designed to accommodate imprecision and qualitative factors, but it does not encompass dependence relations among competences.
Strnad and Guid (2009) presented a fuzzy-genetic analytical model for project team formation, by means of an adaptation of island genetic algorithm considering a single objective optimization model. Differently from their work, in our approach we consider multiple selection variables and see the problem as a multi-objective problem.
Lin (2006) proposed a multi-objective and multistage fuzzy competence set model to overcome the competence selection problem. From different simulations, he obtained a satisfactory solution for evaluation of expansion optimal path cost and benefits. However, in this work is not addressed the relationship among competences and costs.
Wang et al. (2009) proposed a particle swarm optimization method to project for human resource selection in a project organization and they concluded that their method is effective to solve the problem that they studied. However, the author considers neither costs nor dependency among competences.
In the same way, but different perspective, Ligen and Cairong (2009) wrote an index model to evaluate the core of corporate competences, under the light of BSC (Balanced Score Card). Their work established weights that would be used in AHP (Analytic Hierarchy Process) process decision model, and then, build enterprise’s competences evaluation fuzzy key model, applying fuzzy mathematics theory.
Our work differs from the others that we have mentioned, because it considers the combination of four aspects. First, we consider competence an indivisible unit, as a binary value, where 1 means to have the competence and 0 not to have the competence. According to Chen (2006), competences are described in collective, abstract form, for as much as sub-competences are more measurable. Sub-competences consist of a set of observable, specific, behavior-based steps.
In this study, we treat competences under Chen perspective, as an indivisible feature. If the auditor does not have complete sub-competences set, we consider that this auditor does not possess this competence. Chen perspective seems to be more reasonable. To illustrate this affirmative, we can suppose the competence an airplane pilot is composed by 3 sub-competences: takeoff, glide and landing. If the pilot has just the sub-competences takeoff and glide, we cannot say that he has the competence to pilot airplane as shown in figure 3 and 4.

Fig 2. Competent to Fly an Aircraft
Despite we are under Chen’s perspective, our work differs from Chen’s work due to the fact that we approach individual competences, while he approaches corporate competences.
Another unique aspect of this work is that we consider the budget destined to human resources (costs). In the business world, we must say that each auditor in a team represents an additional cost and this cost grows when quantity of auditors in the team grows. If we maximize only competences, the solution algorithm would be useless, because it would not be applied on real context that demands to minimize costs.

Fig 3. Not Competent to Fly an Aircraft
The third difference of our approach is that certain tasks demand specific competences which are indispensable to accomplish the work. These indispensable competences demand a hard constraint on the algorithm. For example, a work needs to operate a kind of device. If there is no competent auditor able to operate the device, the solution is infeasible.
The fourth aspect of our work is that we consider that exist a dependence relationship among some competences. We consider dependence as shown in figure 4 (white and dark nodes). Suppose that there is one auditor in team that possesses competence 86. According the picture this competence requires competence 49. On the other hand, the competence 49 requires competences 31 and 36. Competence 31 requires no additional competence, but competence 36 requires 48. Thus, if the team has competence 86, it must contain also 49, 31, 36 and 48 to be feasible. This example is shown in figure 4 by white nodes. The dark nodes represent the other dependencies that have been considered as a problem constraint. The dependence relationship increases complexity of selection of competences.
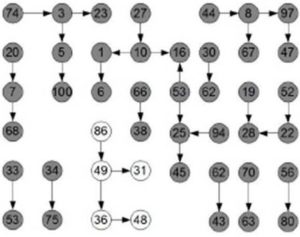
Fig 4. Relationship among Competences
Genetic Algorithms
Genetic algorithms (GAs) are stochastic, population-based search and optimization algorithms inspired by the process of natural selection and genetic (Ahn, 2006). They are, possibly, the first algorithmic models developed for simulating genetic systems. According Engelbrech (2007), GAs were proposed, firstly, by Fraser, and later by Bremermann and Reed et al., but it was the extensive work done by Holland that popularized GAs. That is the reason why Holland is generally considered as the father of GAs.
GAs are inspired on natural selection theory proposed by Darwin in 1859. The main idea of GAs is to arrange possible solutions in individuals (chromosomes) inside a population (solutions groups), and after, using genetic operators, these individuals are recombined to produce offspring.
Genetic Algorithm Developed
The competence selection problem was represented in multi-objective genetic algorithm (GA) developed as described previously and shown in table 1. Figure 6 shows a pseudo-code of the algorithm.
The use of GA is appropriate to solve the competence selection problem because GAs are powerful enough to solve multi-dimensional problems and problems that have more than one solution. Besides, GA possesses an operator called mutation operator. This operator triggers a “dynamic” in the search space, that allow the restoration of lost information and avoids a premature convergence.
Thus, we modeled the problem into a multi-objective optimization problem in a combinatorial scenario, where each objective consists of regarding one constraint. The dependence relationship among competences reinforces the reason for application of a genetic algorithm, because the higher the complexity of problem the better the performance of GA.
One way to solve such an optimization problem is using an exhaustive search. But the large search space, more precisely equal to 2100, and many constraints in this work make this approach prohibitive. On the other hand, heuristic search methods are a good alternative. Despite they do not guarantee an optimum solution, they try to ï¬nd a satisfactory one, using a considerably lower computational effort. That is the reason why we applied genetic algorithms to solve this problem.
In the GA developed, we used a population of 500 chromosomes. This parameter was used in order to avoid a premature convergence and to search in a large space.
In the genetic algorithm developed, firstly, we created randomly the initial population, after fitness and costs were calculated, and finally 15% of population was selected and copied to the next generation. The remaining 85% was applied crossover. The crossover method employed was one-point crossover. We employed tournament selection method. In our approach, we choose randomly five possible parents among population and after, select two of them to apply crossover.
Once ended all crossover process, it was applied mutation in 0.75% of new population. These genetic operators create many infeasible individuals. In order to keep population of feasible individuals, it is used a repair function to fix the offspring population.
After mutation process, we choose 5% of best individuals into population of parents and apply elitism by copying themselves to next generation. According to Engelbrech (2007), elitism refers to the process of ensuring that the best individuals of the current population survive to the next generation. The best individuals are copied to the new population without being mutated.
These operations are repeated until the algorithm reaches 200 generations. Figure 6 depicts the pseudo-code of algorithm developed.

Fig 5. Pseudo-code of GA Developed
As we can see, the algorithm possesses two hard constraints that are detailed in the following section.
The Study
In the study performed, we considered an auditing team as a set A and auditing budget limit Cmax. The auditors team A is a subset of auditors universal set U and it is composed with several auditors a1, a2, a3, …, an. Each element of the set A represents an auditor, thus the quantity of auditors in A, is represented by |A|.
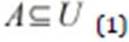
In this work, the set U contains 100 auditors. So, we have a search space equals to 2100.
Each auditor has his own set of competences H, and H comprises competences h1, h2, h3, …, hi, so H = {h1, h2, h3, …, hi}. The auditor’ salary is represented by SA. Following, we show the constraint of maximum cost (2).
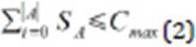
The equation 2 represents the sum of salaries of each auditor that must be less or equal to the budget Cmax. The second constraint treats the indispensable competences. The competence set of auditor’s team Hteam is composed by the union of competence sets of each auditor H. We employed this method because it does not matter if a team has 3 auditors having competence 1 or a single auditor possessing competence 1. Competences duplicated were counted just one time. This rule only applies for indispensable competences evaluation.

In order to satisfy the indispensable competence constraint, consider the set O as indispensable competences set. Thus, this set must be a subset of Hteam, otherwise the solution is infeasible.
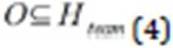
Thus, our algorithm must regard the constraints shown at equations 2 and 4. The other constraint is the dependence among competences and it is represented in the figure 5. In this figure, dependencies are visually represented by arrows.
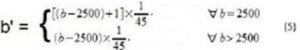
To find the most appropriate solution for competence selection problem, firstly, we created two scales, one scale b’ for values of salary SA and other called c’ for the auditor competences set H. As shown in table 1, the competences of auditors comprise values between 3 and 7. In order to normalize this values, if an auditor has 3 competences, he receive value 1 at scale of benefits and if he has 14 competences he receive value equal to 100, as shown in equation 6. The scale of salaries follow the same idea, but the values vary between 2500 and 7000, where 2500 is reduced to 1 and 7000 to 100 as presented in equation 5.
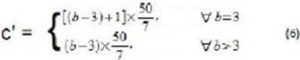
After reducing the values to the scale, we applied the benefit evaluation function. The benefit evaluation function was elaborated by calculating the difference between the quantity of competences of an auditor |H| and his salary SA. In other words, the benefit value Bn was calculated considering the difference between costs c’ and competences b’. Equation 7 shows how we treated the benefits. We add 100 to benefit to avoid negative numbers, working only with natural numbers. This function is shown in equations 8 and 9.
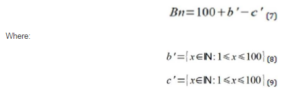
Both b’ and c’ are less or equal to 100 because scale reduction. Therefore, benefit is any value greater than 0 and less or equal to 200. Fitness value comprises the sum of benefits of each auditor selected for the team.
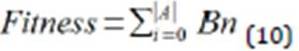
The benefit value was calculated as shown at equations 7, 8 and 9. Due to the fact that fitness comprises the sum of benefits, the objective of GA is to maximize fitness of auditing team. Therefore, greater fitness means better solutions.
Tests Performed
The genes represent auditors and each gene has a set of competences. The sum of competences represents the benefits that we have reduced for a scale (equation 6). These competences are limited, so it’s necessary to show these limits because this feature may impact directly the fitness calculation.
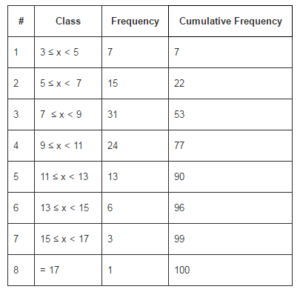
We created a test scenario using settings shown in table 3. In order to develop our work, competences are limited and they are distributed among auditors. Table 1 shows how competences are distributed. For example, we have 24 auditors that possesses between 9 and 11 competences.
Table 1: Competences Distribution
In this scenario, it is necessary to relate competences for creating dependence. There are 27 competences that have 1 dependency. There are 5 competences that have other 2 competences. Figure 4 shows the graph of dependence employed in this work.
Each auditor earns his salary. These salaries are distributed among auditors and it comprises values between 2500 and 7000. Table 2 shows how salaries are distributed.
Using the scenario mentioned, we create 2 types of tests: GA evaluated and random. During GA evaluation, we create 6 test cases {T1, T2, T3, T4, T5, and T6}. In test T1, we chose no indispensable competence and we applied GA for evaluating solutions. In tests T2 and T3, we established indispensable competences. In tests t4, t5, and t6 we used the same parameters used in tests T1, T2, and T3, but T4, T5, and T6 also check dependencies constraints.
Table 2: Salary Distribution

We applied also random test, simple generating individuals only checking max cost constraint. In test R4 we considered the dependence relationship constraint.
In this work, we tested mutation rates equal to 0.5%, 0.6%, 0.75%, 0.85%, 0.9% and 1%. The best performance was reached by 0.85%. Besides, we checked crossover rates 60%, 70%, 80%, 85% and 90%, where the best performance was reached when we apply 85%. Both performance tests mentioned were assessed in worst case scenario. The worst case scenario involves the biggest number of constraints.
Table 3: Tests Settings
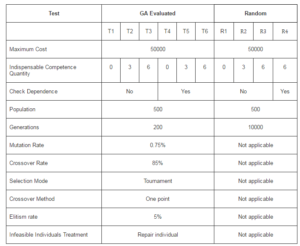
Table 3 shows a summary of settings we used to run tests evolving GA. We repeated the test 30 times, every time using different initial population, in other words, we created 30 instances of test. Then, we compared the outcomes obtained for each instance and selected best result reached.
Results Reached
After running the GA in test case T1, we obtained best fitness value equal to 2109 in an auditor team comprised by 16 auditors. As shown at equations 7, 8, 9 and 10, the fitness of each gene is any value greater than 1 and less than 200.
Considering test T2, we established that competences 2, 4 and 7 are indispensable. The benefits average reached was 132, less than T1. This reduction was generated because, when we determine the existence of these competences constraints, we direct and reduce search space and genes diversity.
In the test T3, the competences 1, 2, 3, 4, 7 and 10 are indispensable. The outcomes reached are similar to test T2, and the average is 131. Table 4 show the results obtained by GA.
Table 4: Results Obtained by GA
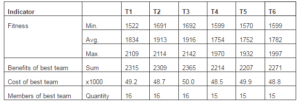
In tables 4 and 5, the benefits of best team comprise the sum of benefits of each auditor that is part of best team reached by GA. For example, in case of T1, this value is the sum of benefits of 16 auditors, which comprises best team. Costs of best team follows the same idea, but these values represent the sum of salary of the 16 auditors selected by GA, at test T1.
On the other hand, we performed random tests R1, R2, R3 and R4 following settings shown in table 3. For each test, we created randomly 5 million of individuals grouped in 500 populations, considering only the cost limit of 50000. In the test R1, we did not establish any competence constraint and we reached a bigger quantity of feasible individuals. In the test R2, we applied the same competence constraint applied in test T2, as well as in test R3, where the competence constraint applied is identical to test T3. We only applied dependence constraint in the test R4. Table 5 shows results generated by random algorithm.
Table 5: Results Randomly Generated
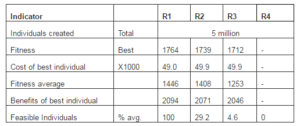
Random tests R1, R2 and R3 do not consider dependency-relationship, when we compare the tests performed, the fitness value reached for GA, in cases T1, T2 and T3, are 31.25%, 13.97% and 15.97% greater than random tests outcomes R1, R2 and R3, respectively. In the test case R4, the random algorithm was not able to generate viable a solution, in other words, all solutions generated by test R4 were infeasible.
When we compare tests R1, R2 and R3 with T1, T2 and T3 which are similar settings, the results reached by GA are betters than random. Comparing T1 and R1, GA result is 19.56% more than random test outcomes. If we measure T3 and R3, the difference is 25.12%. Table 6 shows comparison among random and GA results.
Table 6: Comparison between GA Result and Random Results
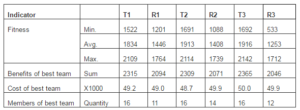
Figure 6 compares the outcomes reached by GA and randomly.
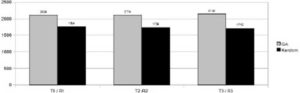
Fig 6. Comparison between GA and Random Outcomes
Conclusion
In this work, we developed a genetic algorithm to solve the competency-based selection problem. We consider three restrictions: the solution involves costs less than the budget, it contains indispensable competences, and obeys dependency-relationship among competences. We performed tests and concluded the random solution is not appropriate to this problem, because when the random algorithm was able to generate some solution, all solutions generated were worse than that reached by GA. In the cases that constraints are harder, the random algorithm was not able to generate any feasible solution. So, the algorithm developed proved to be relevant and essential. When running GA that implements a reparation function, we reached good individuals, showing that the genetic algorithm proposed reaches better results comparing to random selection method. Thus, we conclude that our alternative application of genetic algorithms is an efficient and more effective way to solve the competency-based selection problem.
References
Ahn, C. W. (2006). Advances in Evolutionary Algorithms, Theory, Design and Practice, S.-V. Berlin, Springer-Velarg, Berlin, vol. 18.
Publisher – Google Scholar
Chen, H.- C. & Naquin, S. S. (2006). “An Integrative Model of Competency Development, Training Design, Assessment Center, and Multi-Rater Assessment,” Advances in Developing Human Resources, SAGE, no.10.1177/1523422305286156.
Publisher – Google Scholar – British Library Direct
Engelbrech, A. P. (2007). Computational Intelligence – An Introduction, Wiley and Sons, pp. 143.
Publisher – Google Scholar
Fleury, M. T. L. & Fleury, A. (2001). “Construindo o Conceito de Competência,” Revista de Administração Contemporânea, [online], [retrieved in 2012/10/15], available in http://www.scielo.br/scielo.php?pid=S1415-65552001000500010&script=sci_arttext.
Publisher
Gilan, S. S., Sebt, M. H. & Shahhosseini, V. (2011). “Computing with Words for Hierarchical Competency-Based Selection of Personnel In Construction Companies,” Construction Engineering and Management, Department of Civil and Environmental Engineering, Applied Soft Computing, Elsevier, Volume 12, Issue 2, February 2012, pp 860—871.
Publisher – Google Scholar
Golec, A. & Kahya, E. (2007). “A Fuzzy Model for Competency-Based Employee Evaluation and Selection,” Computers & Industrial Engineering, vol. 52, pp. 143—161.
Publisher – Google Scholar
Hachicha, R. M., Dafaoui, E. M. & El Mhamedi, A. (2010). “A Competence Based Evaluation and Selection Problem by Fuzzy Linguistic Computing,” Proceedings of Computational Intelligence and Design (ISCID) 2010 International Symposium, ISBN: 978-1-4244-8094-4, October 2010, Hangzhou.
Publisher – Google Scholar
Huanga, J.- J., Tzengb, G.- H. & Onga, C.- S. (2005). “Optimal Fuzzy Multi Criteria Expansion of Competence Sets Using Multi-Objectives Evolutionary Algorithms,” Expert Systems with Applications: An International Journal, ACM, vol. 2005.07.033, pp. 739 — 745.
Publisher
Information System Audit and Control Association (ISACA) (2004). “Is Auditing Standard Professional Competence Document #S4,” [online] [retrieved in 2012/10/15], ISACA, available in http://www.isaca.org/Knowledge-Center/Standards/Documents/Audit
Standards/S4CompetencyStandardRevised2Mar05.pdf.
Publisher
Institute of Internal Auditors (IIA) (2010). “Internal Auditor Competency Framework,” IIA Australia, [online], [retrieved in 2012/10/15], available inhttp://www.iia.org.au/Libraries/Learning_Development/Internal_Audit_Competency_Framework.sflb.ashx.
Publisher
Lappas, T., Liu, K. & Terzi, E. (2009). “Finding a Team of Experts in Social Network,” 15th ACM SIGKDD international conference on Knowledge discovery and data mining, ISBN: 978-1-60558-495-9, New York, United States of America.
Publisher
Ligen, Y. & Cairong, Z. (2009). “The Study on Fuzzy Comprehensive Evaluation Model of Enterprise’s Core Competence Based on BSC,” Second International Symposium on Computational Intelligence and Design, ISBN: 978-0-7695-3865-5, Changsha, Hunan, China.
Publisher – Google Scholar
Lin, C.- M. (2006). “Multiobjective Fuzzy Competence Set Expansion Problem by Multistage Decision-Based Hybrid Genetic Algorithms,” Applied Mathematics and Computation, Elsevier, pp. 1402—1416.
Publisher – Google Scholar
Pickett, K. H. S. (2010). The Internal Auditing Handbook, 3rd edition, A John Wiley and Sons, Ltd., pp 99.
Publisher – Google Scholar
Seol, I. & Sarkis, J. (2006). “A Model for Internal Auditor Selection: The Case of a Trading Company in Hong Kong,”International Journal of Auditing, vol. 10, p. 243-253.
Publisher – Google Scholar – British Library Direct
Strnad, D. & Guid, N. (2009). “A Fuzzy-Genetic Decision Support System for Project Team Formation,” Applied Soft Computing, Elsevier, pp. 1178—1187.
Publisher – Google Scholar
Wang, S.- Q., Gong, L.- H. & Yan, S.- L. (2009). “The Allocation Optimization of Project Human Resource Based on Particle Swarm Optimization Algorithm,” IITA International Conference on Services Science, Management and Engineering, ISBN. 978-0-7695-3729-0, Zhangjiajie, China.
Publisher – Google Scholar