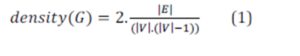Using Mapreduce for Efficient Parallel Processing of Continuous K nearest Neighbors in Road Networks

 Introduction

With the proliferation of wireless communications and positioning technologies (e.g. GPS-Global Positioning System), applications and location-based services (LBS) have emerged and rapidly have gained more attention. A major problem in LBS concerns the search of nearest neighbors (NN). For example, a user in his car searches for the nearest restaurants throughout his path. The response to this kind of queries must be valid at the time of receipt by the user.

So far, the search of the k nearest neighbors (k-NN) is a major problem in data warehouses including data that describe dynamic environments of moving objects.

There are several techniques for processing K-NN search queries in a static data-environment. In Roussopoulos et al.(1995), the authors propose a method for calculating the nearest neighbors in an R-Tree. An alternative based on Voronoi cells was proposed in Berchtold et al.(1998).

Other works (Korn at al., 1996; Seidl and Kriegel, 1998) propose to run through the data set, several times, until the shortest distance is reached. Recently, research has focused on continuous k-nearest neighbors search queries (C-KNN) of moving objects in the context of road network (Lee et al., 2009; Samet et al., 2008).

A continuous query is a query that, instead of being processed only once at the moment of submission to the system, is continuously evaluated during a given time interval (Terry at al, 1992).

With the absence of a standard processing such requests in a dynamic environment, several approaches have been proposed. The challenge is to provide users with valid responses upon receipt.

To meet our goals, formal concept analysis (FCA) seems to be an elegant solution to allow grouping interest points (i.e. moving objects) in a hierarchy of levels.

Each level corresponds to a group of mobile objects that share a common set of properties (e.g., speed, position, direction, etc.). The adoption of FCA in various IT fields, such as knowledge extraction and representation (Lakhal and Stumme, 2005), technologies related areas (Bendaoud et al., 2010) or databases (Rancz and Varga, 2008), has highlighted the importance of concept lattice structures.

Thus, we propose a novel approach to continuous k-NN search which is applied to the road network context. Our contribution is based on a mathematical technique, namely formal concept analysis, in order to present a network abstraction that is based on the neighborhoods. Our approach aims to meet user needs, while considering the road conditions and the user context.

However, the time spent to find the nearest moving objects will exceed the constraints for real-time execution. This also adds more complexity to the FCA-based search method as the complexity of parsing large concept lattice depends on the number of moving objects and the degree of changes in their properties. Thus, this problem becomes especially important and challenging as the number of moving objects in the road network increases.

Similar to most big data applications, the big data tendency also poses heavy impacts on CKNN search systems. Indeed a real road network (modeled as a big complex graph) is composed of a very large set of nodes and their arcs. Each element is characterized by a set of static and dynamic properties (e.g. disturbance factors).

Such properties need to be processed instantly in order to deliver the suitable response (near moving objects) to a user.

Existing methods still cannot support very large road networks (e.g. the whole USA road network). The main limitation of these approaches is either high memory consumption or heavy search overhead.

For example, for the whole USA dataset(24M vertices), we estimate that state-of-the-art approach like ROAD(Lee et al., 2009) needs over 105 days for pre-processing, and SILC (Samet et al., 2008)consumes approximately 618GB memory, which represents a very poor scalability and efficiency on large road networks.

In this paper, we combine the strengths of FCA and MapReduce to present a parallel continuous k-nearest neighbor (CKNN) search method of moving objects in road network and we improve the efficiency of located moving objects by employing the MapReduce paradigm. In particular, our main contributions can be summarized as follows:

Road network partitioning. We divide the road network into a set of smaller search spaces and deliver them to corresponding slaver servers to use their changing conditions in the selection of candidate moving objects.

MapReduce functions based onFormal Concept Analysis. We show how the powerful mathematical method FCA is used to represent the data-related moving objects and to allow their clustering and effective parsing and search. In the Map function, we extract the near candidate moving objects according to their properties using FCA. In the Reduce phase, we merge the candidate moving objects and compute their shortest paths and distance based on their properties as well as the current road data.

Prototype implementation. We show how a parallel programming platform called Storm is used to implement the FCA-based search method.

The rest of the paper is organized as follows: Section 2 presents our previous work. Section 3 gives an overview of the adopted technique. In Section 4, we present our parallel FCA-based approach to the search for k-nearest neighbors in a road network. Section 5 gives some details on the implementation and the performance evaluation of our kNN search approach. Section 6 summarizes the state of the art research methods of k-nearest neighbors in road networks. The last section is devoted to the conclusion and future work.

Previous work

In this section, we give an overview of our previous work(Ferchichi and Akaichi, 2015). In the first sub-section, we start by presenting the Formal Concept Analysis mathematical formalism, we have adopted in our continuous k-nearest neighbor search method approach. The second sub-section presents the main steps of the proposed FCA-based search method.

Formal concept analysis

Formal Concept Analysis (FCA) is a mathematical formalism that provides hierarchically structured concepts and group objects having the same attributes. The resulting hierarchy of the FCA is known as Galois (Barbut and Monjardet, 1970) or concept lattice (Ganter and Wille, 1999). The mathematical foundation of FCA and conceptual structures that can be derived (Godin et al., 1995) have been exploited in several areas, such as classification and information retrieval (Carpineto and Romano, 2005), Web service selection (Azmehet al., 2008), ontology construction (Bendaoud et al., 2010), knowledge extraction (Lakhal and Stumme, 2005), software engineering (Tilley et al., 2005) and (Godin and Valtchev, 2005), linguistics (Priss, 2005), etc. FCA allows building a concept lattice from a binary relation Objects X Attributes (see the next sub-section).

Definition 1 (Formal Context): A Formal Context is a triplet K = (G, M, I) where G is a set of objects, M is a set of attributes and I a binary relation between G and M satisfying: I ⊆ G × P; (g, m) ∈ I with g ∈ G and m ∈ M, g means that the object has the attribute m or m is an attribute possessed by the object g.

Definition 2 (Formal Concept): A Formal Concept of a context K = (G, M, I) is a pair (A, B): A ⊆ G, B ⊆ M, A’ = B and B’ = A, where A’ is the set of all attributes of B possessed by the objects of A and, in a dual way, B’ is the set of all objects having the attributes of B. The sets A and B are called respectively extension (Extent part) and intension (Intent part) of formal concept C. B (G, M, I) denotes the set of all concepts of the context K = (G, M, I).

FCA-based continuous k-nearest neighbor search in road networks

A graph is a suitable candidate to model a road network. As shown in Fig. 1, a graph-based road network, which is considered as the search space, consists of vertices (nodes) that are connected by links (roads connecting the various nodes). The graph contains several static information (edges and nodes) and dynamic information (moving objects together with their characteristics

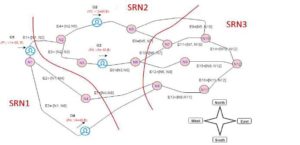
 Fig. 1. Research space at time t = 0

Our FCA-based CKNN search method takes as input a graph-like road network and a set of candidate moving objects with their static and dynamic properties. It consists of the four main steps, described as follows:

Step 1 (road network modeling).The search space or the road network is modeled as a graph G.The aim of the first step is to transform the road network to an abstract graph G. G is composed of a set of nodes N and edges E. The latter carries several types of information: static information (nodes and edges) and dynamic information (moving objects and their characteristics).

Step 2 (Formal context extraction).In our work, the characteristics of moving objects will be delivered in real time to our system. Based on the road information, and on the different characteristics of the moving objects, this step, first, performs the binarization of the moving objects’ characteristics, then the generation of the matrix of formal context from the information extracted from the graph-based road network. We denote by O all the moving objects, and by A the set of their attributes (characteristics of moving objects).

Step 3: (Generation of the lattice of moving objects).  This step takes as input the formal context created in step 2, and generates a lattice of candidate points of interest. Each formal concept in the lattice represents a candidate solution to a given search query. To reduce the time spent in the search within the lattice of moving objects, we propose to index all the concepts in the lattice based on what we call “level of concept”. A level is defined for each generated concept. An index table will be created (Level + concepts) in order to accelerate the search process.

Step 4 (Query Evaluation or answering).This step consists of searching within the generated lattice in order to extract the relevant formal concepts. This allows retrieving the moving objects that can satisfy the user’s query.

The use of FCA for searching the k-nearest neighbors is motivated by two main features: the conceptual structure of the lattice data and the hierarchy between the concepts. The complexity of lattice construction depends on the number of moving objects and their properties.

 The construction of concepts is equal to O(k.m), where k is the number of properties of an interest point, and m is the number of points of interest. The complexity of the search algorithm is equal to O(L) where L is the number of concepts. However, maintaining the relevance of the delivered results mainly depends on reducing the response time, because these results must be valid at the time of their receipt by the user.

To achieve our goals, the proposed approach aims to reduce the search space and the response time by parallelizing the search task. This is achieved with the use of MapReduce parallel programming parading as we will show in the following sections.

MapReduce parallel programming model

In this section, we first describe the basics of MapReduce programming Model. MapReduce is a framework proposed by Google to allow processing highly distributed problems across huge datasets using large number of computers. The distribution of the large amount of data implies parallel computing since the same computations are performed on each CPU, but with a different dataset.

In a MapReduce job, the master node first partitions input data into M independentchunks (where M is the number of Map tasks) and passes them to the mapper nodes. Each map task is independently executed in a mapper node. Afterwards, in the map phase, each mapper generates a series of intermediate key—value pairs based on the input data chunks and according to a user-defined Map function. The MapReduce runtime system then automatically sorts and merges these intermediate key—value pairs depending on the key. The intermediate data with the same key are divided into R segments (where R is the number of reducer nodes) using a hash function. Finally, after being notified of the location of the intermediate data in the reduce phase, each reducer accepts a set of intermediate key—value pairs and merges all the data with the same key value, then generates a series of key—value pairs according to a user-defined Reduce function(Li et al., 2015).

Proposed approach

In this section, we present the proposed framework for continuous k-nearest neighbour search in road networks with MapReduce (see Fig. 2).

Fig. 2. A system overview of the CKNN search approach.

In this figure, ellipses represent road network data, squares represent processing of candidate moving objects and rows show the flow of data.

As shown in Fig. 2, our CKNN search method works as follows:

Input road network is partitioned into Nsub-road networks. Each sub-road network will be processed against the user query by a mapper machine, in order to evaluate the network state and the candidate moving objects that belong to this sub-road network.

Mapper i reads the assigned sub-road network partition and returns the corresponding candidate moving objects that meet the user query. Mapper i outputs key/value pairs of near moving objects.Keys represent properties of moving objects, whereas values represent moving objects.

For each unique intermediate key, the reducer passes the key property and the corresponding set of intermediate values (near moving objects) to the defined reduce function. According to these key/value pairs (in our case properties/candidate moving objects), the reducer outputs the final list of key/value pairs of the k-nearest moving objects after filtering according to the user requirements, and the feasible solutions.

The next sub-sections give more details about each of the above steps.

Density-based road network partitioning method

The motivation behind dividing the road network data into sub-road networks is to reduce effectively the search space by dealing with small graphs of roads.

This allows searching the k-nearest neighbors in parallel fashion. Finally, the intermediate results are combined to get the k-nearest moving objects.

Using this approach, we can decrease the complexity of our previously proposed FCA-based search method(Ferchichi and Akaichi, 2015), as the time complexity of the search process is proportional to the size of the formal context and the concept lattice of candidate moving objects.

However, it is important to adopt an effective partitioning technique to avoid the loss of road network and moving objects information. In addition, the arbitrary partitioning method of MapReduce may be the origin of map-skew which refers to imbalanced computational load among map tasks (Kwonet al., 2012) and consequently to the non-satisfaction of user requirements.

In addition, there is a big difference in the distribution of moving objectsacross the search space. Non-uniform distribution of moving objects would cause many problems.

For example, query response time difference among different areas would lead to difficulties in decision-making. To solve non-uniform distribution problems, we need an intelligent regiondividingmethod to ensure the efficiency of query in different areas and to improve the quality of delivered response.

Considering the fact that the task of CKNN search depends on the road network state and its complexity in terms of roads (considered as arcs in the graph-based modelling), we adopt the density-based method proposed by (Aridhi et al., 2015).

The proposed method consists of constructing partitions (chunks) according to the density of graphs. The goal behind this partitioning is to ensure load balancing and to limit the impact of parallelism and the bias of tolerance rate.The following definitions are used:

Definition 3 (Graph). A graph is a collection of objects denoted as G = (V, E), where V is a set of vertices and E V x V is a set of edges. A graph G”² is a subgraph of another graph G, if there exists a subgraph isomorphism from G”² to G, denoted as G”² G.

Definition 4 (Sub-road network). A graph-based Sub-road network G’ = (V’, E’) is a sub-graph of another graph (the whole road network) G = (V, E) iff V’  V and E”² E.

Definition 5 (Graph density). The graph density measures the ratio of the number of edges compared to the maximal number of edges. A graph is said to be dense if the ratio is close to 1, and is said to be sparse if the ratio is close to 0. The density of a graph G = (V, E) is calculated by

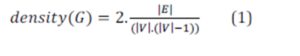
Table 1 shows the density results of partitioning the graph-based road network. The partition of sub-road networkSRN3 is smaller than those of SRN1 and SRN2 because of the possible alternatives offered to moving objects in terms of roads (i.e. arcs).

Table 1: Density example of the three sub-road networks

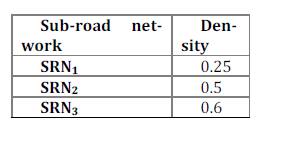
Based on the results of the partitioning step, the moving objects and their characteristics are represented in three Formal Contextsaccording to the number of Sub-road networks. Consequently, three mappers are responsible for the search task within the generated formal contexts, in order to extract the near candidate moving objects.

Due to the space limit in the paper, we only present an example of formal context and lattice derived from the first sub-road networks (see Fig. 3 and Fig. 4).

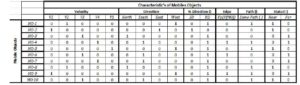
Fig. 3. Formal context of the moving objects assigned to the 1^stmapper

Next, we present the tasks of the Map and Reduce functions for processing the formal context and searching the k-nearest neighbors through the lattice of moving objects.

FCA-based MapReduce functions

In this phase, we apply our FCA-based CKNN search method that we run on each sub-road network in parallel. Algorithm 1 and 2 present our Map and Reduce functions respectively.

FCA-based Map function.In the Map function, the input key/value pair would be like <i, FC_i>, where icorresponds tothe i^th partition ofthe road-network, and FC_i is a formal context representing a set of candidate moving objects at a time t.

As shown in algorithm 1, the formal context FC_iassociated tothe i^th mapper is transformed into a concept lattice L_i of moving objects (line 1). For the construction of the lattice, we use one of the existing algorithms (e.g. Bordat, Next Neighbor) offered with the Galicia (http://www.iro.umontreal.ca/~galicia/) tool.The lattice constructed by the first mapper isshown in Fig5.

Then, for each concept C_j in the latticeL_i, the mapper checks the status of each candidate object (lines 2 and 3), so that it can output the key/value pairs of near objects (line 4).

The output key/value pairs of the Map function would be like

, where P is a set of properties characterizing a set of moving objects, and MO corresponds to the candidate objects that are characterized by the properties P at a time t.

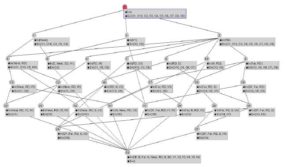
Fig. 4. Generated Concept Lattice of Moving object for the 1^stmapper

After searching within the lattice constructed by each mapper, the output key/value pairs of all the Map functions (see Fig. 5) are then processed in the Shuffle phase and grouped together by key (i.e. characteristics of moving objects).

Finally, one node is chosen to calculate the distance and the shortest path to the candidate moving objects that share the same properties. Note that this phase is out of the scope of this paper, as the movement of data is transparently orchestrated by the adopted MapReduce framework (see section 5).

Fig. 5. Key/value pairs’ outputs of the Map phase

FCA-based Reduce function.The shortest path problem in real-road networks is the cornerstone of the reduce phase in the CKNN search process.

The reduce function receives a set of pairs

that represent the near moving objects (results of the FCA-based Map function after eliminating the far moving objects). The reduce function, then, computes the distance and the shortest path to each near candidate object. Only near objects that have a distancesmaller than a given threshold (specified by the user) will be kept.

In the Reduce function, the input key/value pair would be like

. The Reduce function outputs a sorted list of moving objects according to the calculated distances. We use the distancebetween the query point and a candidate moving object as a key in the outputs of the Reduce function (see Algorithm 2).

To compute the shortest distance between the query point and each candidate near moving object, we adapted Dijkstra algorithm.

According to Denardo [29], Dijkstra algorithm is the most time efficient algorithm for computing the shortest path. Complexity of the computation time is O(nm log(n)), where n is the number of nodes in the graph-like road network and m the number of outgoing arcs of the graph.

The procedure ShortestPathComputation is based on Dijkstra’s algorithm. It takes as input a query point QP and a candidate moving object MO. The procedure output is a shortest path from QP to MO, with its corresponding distance.

The distance is defined by its origin (QP_x, QP_y) and destination (MO_x, MO_y) positions.Note that the distance and path computation is not realized on a separate sub-graph of the road network, but on the initial road network.

As shown in the above algorithm, the reducer starts by calculating, for each near moving object, the distance D and the shortest path to each moving object (lines 2 and 3). Since, several pairs may have the same distance with the query point, the reducer sorts them by distance and according to the number of nodes in the selected path. Finally, the reduce function returns output key/value pairs in the form of, where D is a distancein kmwith respect to a minimum threshold, and Pth corresponds to the shortest path between the query point and the candidate objects MO.

The following is an example of reduce function’s output:

Here the key 5.4 is the distance in km whereas the value {N1, N5, N9, N10, N12} represents theshortest path composed of five nodes.

The final output of this CKNN search process in the road network is an ordered list of the k-nearest neighbors and their positions in the corresponding sub-road network.

In the next section, we present the implementation details of our FCA-based CKNN parallel search approach.

Implementation and parallel CKNN search settings

The implementation of our prototype consists of three phases: (1) the extraction of the formal context, (2) the generation of the lattice of moving objects, and (3) the search of interest points within the generated lattice. Our prototype is implemented with the Java language.

To improve its scalability and efficiency in big data environment, our prototype is implemented on Storm (Toshniwal et al., 2014), a widely-adopted distributed computing platform using the MapReduce paradigm.We choose this platform between other dominant open-source MapReduce frameworks such as Apache Hadoop (http://hadoop.apache.org/) and Spark (http://spark.apache.org/).

Apache Storm is an open source and a fault tolerant framework forprocessing large data inreal time. Storm allows real time data analysis, machine learning,sequential and iterative calculation. It is characterized by itssimplicity, scalability and speed of calculation.

More precisely,it processes the data in the order of one million tuples persecond for each cluster nodes. Following a comparative studyof Stormand Hadoop, we find that the first is geared for BigData applications in real time while the second is effective forbatch applications.

 Also, Hadoop stores its data in the HDFS and thus does not allow iterative computation, whereas Storm allows different resources and iterative computation.

Stormuses the key-value format and support streaming mode (contrarily to Haddop which processes the data in batch mode), which is suitable to the case of continuous search of moving objects with changing properties (e.g. speed, position, etc.) in road networks with dynamic states.

Based on this comparison, we implemented the parallel FCA-based search algorithm using Storm because itis suitable for real time applications.

Regarding the evaluation of the accuracy and scalability of FCA-based CKNN search, to see the impact of the number of moving objects on the complexity of lattice construction and k-nearest neighbors’ extraction, extensive experiments are conducted.

We have varied the number of moving objects (between 500 and 4000) in a road network graph containing 500 nodes (see Fig 6).

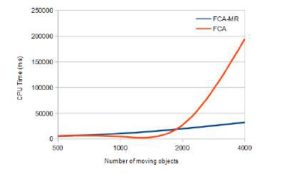
Fig. 6. FCA based search vs FCA-MR based search

Compared to the FCA-based search method, the parallelization of the search (FCA-MR) task significantly reduced processing time. This is explained by the partitioning of the unique context (used in FCA-based method) into a set of formal contexts with reduced sizes (in FCA-MR method). Therefore, the lattice constructed from each small formal context isprocessed in an acceptable time and, hence, complexity is reduced.

Moreover, partitioning the road network graph also reduced the search space (500 nodes in the case of the FCA-based method) unlike our FCA-MR approach, which allows browsing small sub-graphs (e.g. 125 nodes in the case of the first Mapper).

Fig. 6 also shows that, when the number of moving objects exceeds 2000, our FCA-based method is no longer able to return a valid response in a reduced time which violates one of the major constraints in the continuous k-nearest neighbor research problem. The integration of MapReduce logic into our FCA-based method has allowed delivering a valid response inan optimal time(see case of 4000 moving objects).

To ensure that the FCA-MR method maintains an acceptable level of performance even in large scale CKNN problems and to ensure that the processing time will not be affected by the increase in the size of formal contexts, we conducted another series of test by varying the number of moving objects from 5000 to 10000 (see Fig. 7).

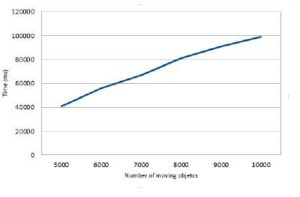
Fig. 7. FCA-MR performance with large number of moving objects

As shown in Fig. 7, the increase in the number of moving objects did not affect the performance of our FCA-MR method. This is explained by the logic of allocating Map and Reduce tasks in Storm. A suitable configuration of blocks’ size in Storm may guarantee partitioning the formal context in small portions of formal contexts.

Related work

To resolve the kNN search problem, several approaches have been proposed. The most common classification of this problem is based on the way the distances between points are calculated, including Euclidean distance and the distance of shortest path.

Multidimensional indexing techniques have been studiedextensively such as the R-tree (Guttman, 1984). Several variants of the R-Tree appeared among them R * Tree (Beckmannet al., 1990) or the X-Tree (Berchtold et al., 1997).

These indexing structures have shown their limits in case of higher dimensions. The work proposed by Song and Roussopoulos(2001) suffers from the quality of results, as it highly depends on the number of examples as input. If the number of examples is small, the result will be wrong. In Khyati and Akaichi(2008), Delaunay triangulation is used for modeling a road network consisting of direct routes joining points of the space. The authors propose to apply a partitioning model in the road search space, by adding weighting factors such as urban traffic, elapsed time, velocity.

Recent attempts, such as Zhonget al.(2013) which propose an index G-tree to find the k-NN at a given location, have shown limitations relative to the size of the studied network.

Most of the above discussed approaches showed shortcomings and are, in most cases, unable to satisfy the users, especially in case of large dimensions or in case of dynamic context. However, the relevance and effectiveness of the expected results depend heavily on the way the search space is indexed and on the research methods used in these indexes’ structures.

MapReduce-based approaches. Recently, the MapReduce parallel programming model has been applied to resolve the kNN problem(Stuparet al., 2010; Yu et al., 2015; Zhu et al., 2015; Ji et al., 2013; Lu et al., 2012).However, they cannot be directly applied to the problem of k-NN search over moving objects, as they suffer from large preprocessing and update costs.

Akdogan et al.(2010) presented a distributed Voronoi index and techniques to answer three types of geospatial queries including reverse nearest neighbor (RNN), maximum reverse nearest neighbour (MaxRNN) and k nearest neighbor (kNN) queries. The location of a point in Voronoi takes extra time. It also incurs high maintenance cost and computation cost when the dimension increases.

SpatialHadoop (Eldawy, 2013)is a MapReduce framework that aims to support k-NN spatial queries. However, itis not suitable to the processing of continuous k-NN queries, since it is not specifically designed for moving objects and because the MapReduce paradigm employed by SpatialHadoop is a batching-oriented processing paradigm and is not good at handling the incremental changes to the query results caused by numerous small updates.

SpatialHadoop does not consider the maintenance cost explicitly, and the index may not work well in the presence of frequent position updates.

Based on the above discussions, our work aims to resolve the majors issues related to exploring the search space as well as reduce the time spent to deliver a response to the user. This is achieved by combining the strengths of Formal Concept Analysis, as a powerful mean of clustering the moving objects—related information, and the processingcapabilities of MapReduce, as a well-known parallel programming model.

Conclusions and future work

In this paper, we have proposed an approach to the continuous k-nearest neighbor search in road networks using a synergy between Formal Concept Analysis and MapReduce parallel programming model. The proposed method relies on a density-based partitioning technique that considers road network characteristics. It uses the densities of roads in order to partition the search space. Such a partitioning technique allows a balanced computational load over the distributed collection of machines and replaces the default arbitrary partitioning technique of MapReduce.

The proposed method allows creating, from a partitioned graph-based road network, a set of formal contexts to be used in the construction of the corresponding concept lattices. These later represent the hierarchy of characteristics of the candidate moving objects.

 Once built, the step of searching points of interest in each lattice can be performed by a set of Mappers in a parallel fashion, through a classification scheme offered by the generated lattice of moving objects. Finally, the extracted concepts in the map phase are processed by the Reducers in order to return the nearest objects.

The mathematical foundation of FCA method has ensured a high level of accuracy and trust in the delivered answers. Also, the MapReduce framework was used to effectively deal with the highly distributed CKNN search problem across huge number of moving objects.

In the future work, we will study the influence of disturbance factors (e.g. traffic jam, accident) on the quality of delivered responses. We, also, intend to validate our approach through a set of experiments.

References

1.    Aridhi, S., d’Orazio, L., Maddouri, M., & Nguifo, E. M. (2015), “Density-based data parti-tioning strategy to approximate large-scale subgraph mining”. Information Systems, 48, 213-223.
Publisher– Google scholar

2.    Akdogan, A., Demiryurek, U., Banaei-Kashani, F., and Shahabi, C. (2010). “Voronoi-based geospatial query processing with mapreduce. InCloud Computing Technology and Science (CloudCom), IEEE Second International Conference on (pp. 9-16).

3.    Azmeh ,Z., Huchard, M., Tibermacine, C., Urtado, C., and Vauttier, S., (2008), “Wspab: A tool for automatic selection & classification of web services using formal concept analysis”. IEEE Sixth European Conference on Web Services, pp. 31-40.

4.    Barbut, M.  and Monjardet, B., (1970), “Order and classification, algebra and combinatorics”. Hachette, Paris.

5.    Beckmann, N., Kriegel, H.P., Schneider, R., andSeeger, B., (1990),“An efficient and robust access method for dots and rectangles”, In Proc.ACM SIGMOD, Atlantic City, NJ, USA, pp.47-57.

6.    Bendaoud, R., Toussaint, Y., and NapoliA., (2010),“The Formal analysis of concepts at the service of building and enriching a ontologie”,.Revue of New Information technology, pp. 133-164.

7.    Berchtold, S., Ertl, B., Keim, D.A., Kriegel, H.P., and Seidl, T., (1998), “Fast nearest neighbor search in high-dimensional space.”IEEE Intl. conf. on Data Engineering (ICDE), pp. 209-218.

8.    Berchtold, S., Böhm, C., Keim, D.A., and Kriegel, H.P., (1997), “A cost model for Nearest Neighbor search in high-dimensional data space”. In proceedings of the sixteenth ACM SIGACT-SIGMOD-SIGART symposium on Principles of database systems, pp. 78-86.
Publisher– Goodle scholar

9.    Carpineto,C., Romano,G., (2005),“Using concept lattices for text retrieval and mining. In: Formal Concept Analysis”, pp. 161-179, Springer Berlin Heidelberg.
Publisher – Google scholar

10.    Denardo, E.V., (1982),“Dynamic Programming: Models and Applications”. Prentice Hall, Englewood Cliffs, NJ.

11.    Eldawy, A., (2013), “A demonstration of spatialhadoop: An efficient mapreduce framework for spatial data” in VLDB.

12.    Ferchichi, H., Akaichi, J., (2015), « Une approche basée sur l’analyse formelle de concepts pour la recherche en continue des K plus proches voisins dans les réseaux routiers ».  Spatial Analysis and GEOmatics (SAGEO): 239-253.

13.    Ganter, R.B. and WilleR.B., (1999), “Formal Concept Analysis”. Springer, mathematical foundations edition.

14.    Godin, R., Missaoui, R., and Alaoui, H., (1995), “Incremental concept formation algorithms based Galois (concept) lattices ». J. Computational Intelligence, vol. 11 (2), pp. 246-267.
Publisher – Google scholar

15.    Godin, R. andValtchev, P., (2005), “Formal concept analysis-based design class hierarchy in object-oriented software development. Formal Concept Analysis”, pp. 304-323. Springer Berlin Heidelberg.

16.    Guttman, A., (1984), “R-Trees: A dynamic index structure searching for space”, ACM SIGMOD, Boston, Massachusetts, USA.
Publisher – Google scholar

17.    Ji, C., Hu, H., Xu, Y., Li, Y., & Qu, W. (2013),“Efficient multi-dimensional spatial RKNN query processing with mapreduce”. In ChinaGrid Annual Conference (ChinaGrid), 8th (pp. 63-68). IEEE.

18.    Korn, F., Sidiropoulos, N., FaloutsosC., Siegel, E., and Protopapas, Z., (1996),“Fast nearest neighbor search in medical image database”. Intl. Conf. on Very Large Data Bases, pp. 215-226.

19.    Kwon, Y., Balazinska, M., Howe, B., Rolia, J.A., (2012),“Skew tune: mitigating skew in mapreduce applications”, in: Proceedings of the 2012 ACM SIGMOD International Conference on Management of Data, pp. 25—36.
Publisher – Google scholar

20.    Khayati, M., Akaichi, J., (2008), “Incremental Approach for Continuous k-Nearest Neighbors Queries on Road”, J. Intelligent Information and Database Systems, Inderscience Publishers, vol. 2, no 2, p. 204-221.
Publisher – Google scholar

21.    Lee, K. C. K., LeeW.-C., and ZhengB., (2009),“Fast object search on road networks”. In EDBT, pp. 1018—1029.
Publisher – Google scholar

22.    LakhalL., StummeG., (2005),“Efficient mining association rules of formal concept analysis is based. In Formal concept analysis”, pp. 180-195, Springer Berlin Heidelberg.

23.    Lu, W., Shen, Y., Chen, S., and. Ooi, B. C, (2012), “Efficient processing of k nearest neighbor joins using MapReduce,” Proceedings of the VLDB Endowment, vol. 5, no. 10, pp. 1016—1027.
Publisher – Google scholar

24.    Li, R., Hu, H., Li, H., Wu, Y., & Yang, J. (2015). “MapReduce Parallel Programming Model: A State-of-the-Art Survey”. International Journal of Parallel Programming, 1-35.

25.    Priss, U., (2005), “Linguistic applications of formal concept analysis. Formal Concept Analysis”, pp. 149-160, Springer Berlin Heidelberg.

26.    Rancz, K.T.J., and Varga,V., (2008), “A method for mining functional dependencies in rela-tional database design using FCA”. Studia Universitatis Babes-Bolyai Cluj-Napoca, Informatica, 53(1), 17-28.

27.    Roussopoulos,N., KelleyS., and VincentF., (1995),“Nearest neighbor queries”. SIGMOD ACM Symp. on the Management of Data.
Publisher – Google scholar

28.    Samet, H., Sankaranarayanan, J., and AlborziH., (2008),“Scalable network distance browsing in spatial databases”. In SIGMOD Conference, pp. 43—54.
Publisher – Google scholar

29.    Seidl, T. and Kriegel,H. P., (1998), “Optimal multi-step K-nearest neighbor search”. SIGMOD ACM Symp. on the Management and Data, pp. 154-165.
Publisher – Google scholar

30.    Song, Z., and Roussopoulos, N., (2001), “K-nearest neighbor search for moving query point”, In SSTD, Heidelberg, Berlin.
Publisher – Google scholar

31.    Stupar, A., Michel, S., and Schenkel, R. (2010). “RankReduceprocessing k-nearest neighbor queries on top of MapReduce”. In Proceedings of the 8th Workshop on Large-Scale Distributed Systems for Information Retrieval (pp. 13-18).

32.    Toshniwal, A., Taneja, S., Shukla, A., Ramasamy, K., Patel, J. M., KulkarniS., JacksonJ., GadeK., Fu, M., Donham, J., BhagatN., MittalS., and Ryaboy, D., (2014),“Storm@twitter”. In Proceedings ACM SIGMOD International Conference on Management of Data, SIGMOD ’14, pp. 147—156, New York, NY, USA. ACM.
Publisher – Google scholar

33.    TerryD., GoldbergD., NicholsD., and OkiB., (1992),“Continuous queries over append-only databases”. ACM SIGMOD Symp. on the Management of Data.
Publisher – Google scholar

34.    Tilley, T., Cole, R., Becker, P., andEklund, P., (2005), “A survey of formal concept analysis for supporting software engineering activities. In Formal concept analysis”, pp. 250-271. Springer Berlin Heidelberg.

35.    Yu, Z., Liu, Y., Yu, X., and Pu, K. Q. (2015). « Scalable Distributed Processing of K Nearest Neighbor Queries over Moving Objects”. Knowledge and Data Engineering, IEEE Transactions on, 27(5), 1383-1396.
Publisher – Google scholar

36.    Zhu, P., Zhan, X., and Qiu, W. (2015). “Efficient k-Nearest Neighbors Search in High Di-mensions Using MapReduce”. In Big Data and Cloud Computing (BDCloud), IEEE Fifth Interna-tional Conference on (pp. 23-30).

37.    Zhong,R., Li, G., Tan, K.-L., and Zhou, L., (2013), “G-tree: an efficient search index for knn on road networks”. In CIKM, pp. 39-48
Publisher– Google scholar