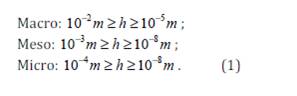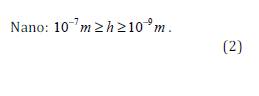Continuum as a basic notion in mechanics of materials
A physical body (piece of raw material) is modeled in mechanics in some steps [see, for example, fundamental book by Ilyushin (1990)]. First, this body is considered within the framework of analytical mechanics as the system of great number of interacting particles. But, the mechanics of solids is interested in macroscopic motion (equilibrium), for which the individual motions of each of particles gives any information. In this case, the methods of other branch of physics, statistical mechanics, that describe the statistics of motion and the interaction of atoms, become very useful. They make possible the evaluation of all necessary in solid mechanics macroscopic parameters, when the great number of atoms (usually, 1 cm3 of material includes about 1022 atoms) interact. The statistical mechanics assumes the macroscopic properties of the system of atoms in the form of the averaged statistical properties. Note here that the averaged statistical value of a given function over the area is called the expectation value of this function over the area. So, statistical mechanics introduces the notions of equilibrium ensemble and Gibbs equilibrium ensemble. Then, the ergodic theorem is used that states: the averaged value over ensemble is equal to the averaged value over time. In such a way, the statistical mechanics gives the averaged (macroscopic) values of parameters used in the solid mechanics and provides transition to the models of solid mechanics. First of all, the principle of continualization is applied, which consists in that the physical body with fuzzy boundary is changed on the fictitious body (area of three-dimensional space, which is continuously filled by geometrical points) of the same form with fixed boundary. Then the macroscopic density of mass is evaluated at any point of fictitious body. The substance, in each point of which the macroscopic density is given, is called material continuum or continuum. Thus, the physical body is transformed into the body as a notion of solid mechanics.
Note that the procedure of averaging is based on the introduction of the notion of representative volume (cube). This volume is chosen in the real body in condition that the sizes of the volume are smaller on several orders of sizes of the body. At that, this volume must include a great number of atoms (particles) for providing the validity of procedure of averaging. The averaged properties of the volume are usually attributed to the point at the volume center. As a result, the averaged properties are evaluated at every point of the body and they should be constant or variable — the body becomes the homogeneous or inhomogeneous one.
Very often, authors of different publications on materials are showing the color pictures of representative volumes in the form of cubes filled of discrete particles, which are looking very nice, but do not image the real discrete structure. For example, such nice pictures of representative cube for polycarbonate and polyimide can be seen in the characteristic of these kinds of pictures’ publication of Valavala et al (2007). Both materials are utilized in composite materials as the polymer matrix.
Note. The authors of the present article apologize to readers that the necessary for the journal written permissions for 18 included into the manuscript figures can not be obtained by authors for the short time. Therefore, the pictures are removed from the article and are only shortly described by words. But, corresponding publications are shown and an inquisitive reader can find these pictures there.
Some words about composite materials
Let us recall that the composite materials are conventionally defined as consisting of several components (phases) with differing physical properties, when the components are alternated many times in the space. The internal structure of composites is formed by the way of alternation of components, conditions on the interfaces, physical properties and geometrical form of components. The usual practice in the mechanics of composites is to represent the components (matrix as a binder and fillers as reinforcing elements) in the continuum approach. Most often, the separately taken component is considered as a structurally homogeneous one. For example, fillers in elastic granular materials are modeled mainly as the spheres made of elastic material with the given density, Young and shear moduli and other physical properties. Thus, the composite materials are thought as the structurally inhomogeneous continuums and can be studied within the continuum approach, when the concrete problems are solved mathematically with the aim of differential equations with discontinuous coefficients.
On this stage of study, the next principle becomes useful — the principle of homogenization. This principle consists in modeling the piece-wise homogeneous medium, deforming of each pieces of which is described by relationships of continuum mechanics of solids, by the homogeneous continuous system (medium) and determination of necessary averaged properties within the framework of the homogeneous continuous medium.
Thus, two basic continuum models are used in the mechanics of composite materials: the model of homo-geneous body with averaged properties and the model of the piece-wise homogeneous body with averaged variable properties.
The real view of the upper side of the representative volume of two variants of syntactic foam sample with fine scale is represented in the very interesting publication of Gupta (2007).
Let us note that from the stated above principles of continualization and homogenization, their principled distinction and methodological commonality follow (especially, in relation to the initial systems, to which they are applied).
Let us note finally that the procedures of continualization and homogenization are realized by means of different methods of averaging. At that, as a rule, the notions of representative volume or elementary volume are used.
Feature 1: Invalidity of the principle of continualization in some types of nanoformations used as fillers in nanocomposite materials
The approach to materials based on the principle of continualization was re-comprehended in the twentieth century, when the mechanics of composite materials was thrive. First of all, the importance of the internal structure of materials was accepted. For this goal, the geometrical parameter λ was introduced, which characterizes the mean value of minimal diameters of granules for materials of granular structure, minimal diameters of cross-sections of fibers for materials of fibrous structures, minimal thicknesses of layers for materials of layered structure. This resulted in the division of the mechanics of materials on macro-, meso-, and micromechanics. For each part of mechanics, the limits of variations of parameter λ were proposed:
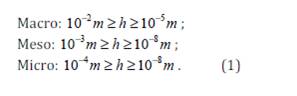
A progress in nanotechnologies made possible the processing of nanocomposite materials and development of theoretical analysis of this kind of materials. At present, classification (1) is supplemented by the next formulation:
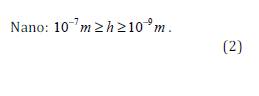
Let us note that the atom level (distance between atom planes in crystal lattice) has the order one or more angstrom (10-10 m); therefore, the nanolevel in (2) is conditionally bounded by 10-9 m.
Consider now the most known type of nanoformations: the carbon nanotube (CNT). The term “nano-tube” was used for molecules-fullerenes with the large number of carbon atoms 10,000 – 1000,000. They are divided on two types: the single-walled (SWCNT) and the multi-walled (MWCNT). The SWCNT can be imagined as the carbon molecular layer (graphite), which is as if rolled into the cylindrical tube. There are many good publications with excellent electronic pictures of real SWCNT’s and MWCNT’s. For example, quite legible pictures of the SWCNT, 4-layer, 6-layer and 10-layer MWCNT in the matrix, can be seen in the popular encyclopedic book on polymer nanocomposites by Mai and Yu (2009).
The very impressive picture of the 15-layer nanotube in the matrix can be found in the professional work of Zhang and Li (2009).
It seems to be worthy to recall here the carbon nanotubes, which by technology of manufacturing are identified as the cup-stacked type carbon nanofibers (CSNF). Some facts about these nanofibers were reported in two publications by Endo et al (2002 and 2003). These fibers are presented in the mentioned publications both schematically, and in the tunneling electronic microscope pictures. The CSNF are produced in Japan by corporation GSI CREOS and have the commercial name CARBERETM. The technology of producing the CSNT can be described as follows. First, the shells in the form of hollow truncated cone are forming from a graphite net. Further, the shells are embedded one into another and then joined. In this way, the hollow cylinder of circular cross-section is formed, which consists of the big number of truncated cone shells. In this technology, the thickness of CSNT is defined by difference of radiuses of the top and bottom cross-sections of conical shell. The external diameter is 50-150 nm, the internal diameter can reach 60% of the external one. The cross-section is about circular, the maximal length of this compound fiber can reach 200 μm, but the mean value is about 30 μm.
It should be noted that interaction between the separate conical layers is realized owing to interaction between carbon atoms, belonging to the separate conical layers.
Let us recall now the more complex nanoformations — the MWCNT ropes and lattices. They can have diverse shapes and structures. The very demonstrative in this sense are the Wagner’s internet-publications. In particular, the Wagner class (2009) proposed a series of the real ropes of multi-wall nanotubes: the fiber of single twine, of the double twine, the fiber from four fiber of single twine.
The nanolattices should be mentioned here also. They consist of hundreds of twisted nanotubes and look very impressive. A good example of real nanolattices gives the book on polymer nanocomposites by Mai and Yu (2009).
Note that the SWCNT and MWCNT with conditionally a small number of layers contain in their cross section absolutely insufficient a number of atoms-particles to provide the procedure of continualization according to the ergodic theorem. These nanotubes not only do not include the necessary number of atoms to form the representative volumes, but each nanotube in whole does not include the necessary number of atoms to be continualized. Thus, continualization of such kinds of CNT’s can not be substantiated and transition from the discrete structure to the continuum description is made from despair. On the other hand, it is impossible to describe the CNT’s within the framework of solid mechanics (for example, by introducing density, Young and shear moduli etc) without a change in the discrete structure on the hollow or solid cylinders. This clear lack of correspondence with the accurate scientific approach is partially filled by experimental methods of determinations of density, Young and shear moduli and other parameters of solid mechanics.
To the point, the first direct experiment to measure the mechanical property is shown in the Wagner class (2009). This is the experiment on the free-standing room-T vibrations of SWNT as clamped cantilever in a tunneling electron microscope. Wagner shows also in the Wagner_class (2009) another scheme of tests. The tests consist in that SWCNT is attached to two atom-force microscope cantilevers and pulled. The deflection of the cantilevers is measured; the force is obtained via Hooke’s law.
So, a lot of reported pictured evidence that the principle of continualization is rather valid for nanoropes, nanowires, nanolattices and other more representative nanoformations.
Note that the continualization in nanomechanics is realized within the approach “bottom- up” that is characteristic just for nanomechanics.
The approaches “bottom-up” and “top-down” are generally known in technology. Sometimes, “bottom-up” is commented as “nucleation and growth”, and “top-down” is commented as “comminution and dispersion” [see, for example, the excellent e-book of Ramsden (2010)].
The approach “bottom-up” consists in the making of materials, starting with the smallest particles up to more massive formations. In this approach, the most essential is the basis — the aggregate of smallest particles and their character. The basis forms the foundation for constructing the more massive volumes of material. This basis is called the bottom.
Transition from description of nanotube as the discrete system and the discrete matrix to the nanotube as the continuum nanorod-fiber in the continuum matrix can be meant as transition from the continuum bottom (atoms of nanotube and matrix) to the more massive formation — structural part of the nanocomposite material.
This is looking as opposite to the procedure of forming the continuum macro (meso, micro) rod-fiber in the continuum matrix of the composite materials. Here another approach is used — the approach “top-down”. It consists in the making of materials, starting with the large volumes of material (bulk materials, source of raw materials) in direction to the smaller formations (pieces) of material. The rough material is pressed, cut, found or in some different way formed into pieces or products. In this approach, the most important is the tool resources, by which the lower limit in sizes of product or material piece is determined.
So, the continuum micro (meso, micro) rod-fiber is formed of the bulk material that is continualized on the scientific base, when the ergodic theorem is valid and all averaged parameters are evaluated on the substantiated positions.
Thus, continualization of nanoformations seems problematic in many cases and their physical properties both evaluated and determined from the indirect tests should be considered critically. This forms the first basic feature of continuum description of nanocomposite materials from the point of view of mechanics of materials. This feature of the continuum description of nanoformations can be taken into account while the nanocomposite materials being studied.
Feature 2: Transition from the two-component structure to the three-component structure
When the nanoformations and matrix are united into a nanocomposite, the phenomena occur on interfaces with participation of more deep-laid mechanisms that it takes a place, for example, in the case of micro-composites. The point is that in the general case, the nanoformations (for example, MWCNT’s) consist of a system of curvilinear layers, in turn each layer consists of a system of atoms, interaction among which is determined by force of interatomic interaction. Therefore, when the nanoformations and matrix being composed into a nanocomposite, then seemingly the interaction of atoms of the “end” layer of atoms on nanoformation with the neighboring atoms of polymeric matrix must occur owing to forces of interatomic interaction.
Thus, some intermediate layer arises from materials of nanoformations and polymeric matrix, inside of which the interaction of atoms of nanoformations and polymeric matrix is observed.
This forms an essence of the second feature of the two features presented in this communication.
Both the first feature of continuum description of nanocomposite materials and the second one are associated with specific property of nanoformations: they have a molecular structure, in which most parts of atoms are located at the surface, and therefore the nanoformations are active and interact with the molecules of the matrix. This can be seen very clearly from the analysis of the different kinds of nano-formations. Let us continue an analysis of the most known type of nanotubes — carbon nanotubes.
First, the existence of a feature in hand was reported and commented by Windle in his personal view Windle (2007). It seems therefore to be fair to cite two important paragraphs from this publication.
“The second moment which defined the meeting for me came towards the end. It was Catherine Brinson’s paper on the effect of nanotubes on the physical properties of the surrounding resin which caught my attention. She compared the influence of nanotubes on composite properties with other types of nanoparticles, and emphasized the point that the huge specific surface area of nanosized particles means that a large proportion of the surrounding polymer is very close indeed to an interface, or in her parlance, much of the matrix is in fact an interface, with properties different from the bulk matrix”.
“Hence the volume fraction of polymer having its properties changed by the nanoparticles (the “inter-face” as described by Prof. Brinson) is very significant indeed. Very approximately, for each 10% of nanofillers that is added to a composite, about 30% of the matrix will have its properties modified! But also, as loadings approach 30% a significant proportion of polymer molecules will be attached to more than one nanoparticle. No wonder it is so difficult to mix more than 15% nanotubes into a polymer melt. So much for nanoparticles, what about nanotubes? … Here we have to ask ourselves the hard question: as to whether there is any reason why unaligned CNTs should enhance mechanical properties of a composite more than nanoparticles of carbon black or silica? An implication of this question is whether reinforcement in nanocomposites, as understood from conventional fibre composite theory, may be a secondary effect only.” Thus, the CNTs transform about 30% of the matrix into the new material with modified properties as compared with the matrix properties.
In this connection, three examples relating to this new feature of nanocomposite material can be proposed.
The first example can be seen in the fundamental polymer nanocomposites handbook by Gupta et al (2008). It shows “the side-walled cross-linked nanotubes into the polymer in a mode that could be more fully integrated and where the system is hybrid polymer”.
The second example can be seen in the NASA report by Frankland and Harik (2002). It illustrates a closeness of CNT’s outer atoms to the molecules of polymer matrix and shows schematically the molecular structure of nanocomposite crystallic polyethylene – CNT.
Note also that the problem of integrating the nanotubes into the polymeric matrix is discussed in the mentioned above handbook of Gupta et al (2008). In particular, the authors wrote at page 215: “There are numerous approaches where nanotubes can be part of the polymeric formulation, but the length of the polymer linkage may limit the ability of each nanotube to be integrated. The chains may react with themselves or may react with the nanotube, thereby limiting the development of the new formulation and its use in the polymer.”
The third example can be seen in the book on polymer nanocomposites by Mai and Yu (2009). It represents the CNT pulled out from the matrix. It is shown that a thin layer (about 3 nm) of polymeric material (matrix) adheres to the surface of CNT. This example illustrates an existence of formation as if new fiber consisting of the core-nanotube and not small interface between CNT and matrix.
The following examples show one more kind of nanoformations: “bristled” (“whiskerized”) nanofibers-nanowires and “bristled knedel-like” nanogranules. The bristled nanowires are thought as nanowires covered by long nanohairlets.
For the first time, such nanowires were reported in publication by Wang et al (2004). The basic wire consists of material CdTe. The covering of basic wire system of nanohairlets is formed from silica SiO2. The authors called such constructions “the bristled nanocentipedes”. This publication reported two kinds of nanocentipedes distinguished by the way from stabilization of the construction as a whole. The Fig.2A from Wang et al (2004) shows the first type of nanocentipedes in the form of bristled construction with the great number of almost parallel hairlets, which grow perpendicular to the basic fiber surface. The system “basic nanowire of CdTe — covering of nanohairlets SiO2” consists in fact of three components: basic nanowire of CdTe forms the solid core-fiber, which is jointed with covering of hairlets SiO2 in the form of so-lid shell, which, in turn, is covered by hairlets (bristle). The Fig.2A case corresponds to the core radius 3nm, the shell thickness
15 nm, and the hairlet length 32 nm.
Note that producing the new nanoformations is related traditionally to the area of activity of physics-chemists and specialists from material sciences and this direction is aggressively developed. In particular, the process of making the covered by hairlets nanoparticles and nanofibers is continued up to now.
As an example, the publication Brinkmann et al (2009) can be pointed out, where the making of covered by nanohairlets nanofibers from polyalkyltiorene (P3AT) is reported. This publication shows the obtained on tunneling electronic microscope image of nanofiber made of P3AT of chemical structure, which is indicated at the left upper angle of image.
This image shows the nanoformation, which is identical to the geometrical shape with the image from Wang et al (2004).
The following example is related to the granular nanocomposites filled by micelles of the sphere-like shape. Such type of nanoformations was reported in the article of Nystrom et al (2009).
The shell cross-linked knedel-like micelle (in terms of Nystrom et al (2009)]) consists of a mixture (fifty-fifty in weight) of polymers PEG-g-PAA-b-(PPF-co-PS) and PFCE. This micelle is self-created, when the nanopure water being added into mixture. The diameter of polymeric micelle is equal to 17-18nm; the diameter of knedel-like micelle is equal to 22-26 nm. Diameters of hairlets are not shown, but it is known that the hairlets should correspond to sizes of atoms from the chain.
It seems to be quite appropriate to note that tradition to give the non-standard names for the covered by nanohairlets nanoformations (fibers and granules) is started in microformations, in which the micro hairlets and covered by microhairlets fibers are named whiskers and whiskerized fibers, respectively [see, for example the publications of Guz and Rushchitsky (2013a, 2013b)].
As it was noted above, the covered by nanohairlets from the chain nanowires named by authors in Wang et al (2004) bristled nanocentipedes. The covered by nanohairlets nanogranules (micelles) named knedel-like nanogranules (in terms of scholars created these nanogranules [Nystrom et al (2009), Ladden (2009)].
Most likely, the authors of the publication Brinkmann et al (2009) were not known by the existence of the cited above names and then named the structure of obtained P3AT-nanofibers covered by nanohairlets as the shish-kebab-like.
Seemingly, some part of physics-chemists likes this name, because it is noted in the publication by Brinkmann et al (2009) that before the structure of shish-kebab type was described by other authors (physics-chemists too) for fibers made of polyolefins.
Thus, the real nanocomposites reinforced by nanofibers and nanogranules require new more complicate as compared with macro (meso, micro) level composites, models. Such models are offered and discussed by authors in the book Guz and Rushchitsky (2013a) [7]. They include three or four components and permit to evaluate the averaged physical constants of nanocomposite materials.
Final conclusions
To begin with, let us note that this paper is based on the recently published book by the authors Guz and Rushchitsky (2013a) and the invited review article by Guz and Rushchitsky (2013b), but, in contrast to them, it includes some new observations and statements. First of all, the here presented two features are formulated probably at the first time as the basic ones from the point of view of the mechanics of materials. They essentially differentiate between the nanocomposite materials and the composite materials of macro- and micro-levels, where such features were not observed.
The first feature testifies the impossibility of substantiation of continuum approach for some classes of nanofillers. The second feature reflects the impossibility to describe correctly the mechanical behavior of nanocomposites by the classical two-component models.
Acknowledgments
Materials of this article were reported at the 6th international symposium “Trends in Continuum Physics” (TRECOP-2014) (Poland, Poznan, 3-7 May, 2014) as the invited plenary lecture. Authors gratefully acknowledged the organizers of TRECOP-2014 Prof. A. Maruszewski and Prof. K. Wojciechowski for the kind invitation and opportunity to report the author’s understanding the basic aspects of nanomechanics of composites.
References
1. Brinkmann, M., Chandezon, F., Pansu, R.B., and Julien-Rabant, C. (2009) “Epitaxial growth of highly oriented fibers of semi-conducting polymers with shish-kebab-like superstructure,’ Advanced Functional Materials, 19 2759-2766.
Publisher – Googlescholar
2. Endo, M., Kim, Y.A., Hayashi, T., Fukai, Y., Oshida, K., Terrones, M., et al. (2002) “Structural characterization of cup-packed-type nanofibers with an entirely hollow core,” Appl. Phys. Letters, 80 (7) 1267-1269.
Publisher – Googlescholar
3. Endo, M., Kim, Y.A., Ezaka, M., Osada, K., Yanagisawa, T. Hayashi, T. et al (2003) “Selective and efficient impregnation of metal nanoparticles on cup-stacked-type carbon nanofibers,” Nano Letters, 3 (6) 723-726.
Publisher – Googlescholar
4. Frankland, S.J.V., Harik, V.M. (2002) “Analysis of carbon nanotube pull-out from a polymer matrix,” NASA CR-2002-211743, ICASE Report No.2002-23.
Googlescholar
5. Gupta, N. (2007) “A functionally graded syntactic foam material for high energy absorbtion under compression,” Materials Letters, 61 979-982.
Publisher – Googlescholar
6. Gupta, R.K., Kennel, E. and Kim K.-J. (Eds) (2008) Polymer Nanocomposites Handbook, CRC Press, Taylor & Francis Group, Boca Raton, USA.
7. Guz, A.N. and Rushchitsky, J.J. (2013) Short Introduction to Mechanics of Nanocomposites, Scientific & Academic Publishing, Rosemead, CA, USA.
8. Guz, A.N. and Rushchitsky, J.J. (2013) “Some fundamental aspects of mechanics of nanocomposite materials,” J. of Nanotechnologies, 24, special issue “Nanocomposites 2013” 1-15.
Googlescholar
9. Ilyushin, A.A. (1990) Mechanics of Continuum, Moscow University Publishing House, Moscow. (in Russian)
10. Ladden, S. (2009) “Knedel-Like Nanoparticles,” Math.-Wiss. und Werkstofftechnik, 40 (3) 45.
11. Mai, Y.-W. and Yu, Z.-Z. (Eds) (2009) Polymer Nanocomposites, Woodhead Publishing Limited, Cambridge, UK.
12. Nystrom, A.M., Bartels, J.W., Du, W.-J. and Wooley, K.I. (2009) “Perfluorocarbon-Loaded Shell Crosslinke Knedel-Like Nanoparticles: Lessons regarding Polymer Mobility and Self-Assembly,” J. Polymer Science: Part A: Polymer Chemistry, 47 1023-1037.
Publisher – Googlescholar
13. Ramsden, J. (2010) Nanotechnology, Ventus Publishing ApS, Copenhagen-London.
14. Valavala, P.K., Clancy, T.C., Odegard, G.M. and Gates, T.S. (2007) “Nonlinear multiscale modeling of polymer materials,” International J. of Solids and Structures, 44 1161-1179.
Publisher – Googlescholar
15. Wagner_class_14 2009-last.pdf
16. Wang, Y., Tang, Z., Liang, X., Liz- Marzan, L.M. and Kotov, N.A. (2004) “SiO2- coated CdTe nanowires: bristled nanocentipedes.” Nano Letters., 4 (2) 225-231.
Publisher – Googlescholar
17. Wilson, N., Kannangara, K., Smith, G., Simmons, M. and Raguse, B. (2002) Nanotechnology. Basic Science and Emerging Technologies, Chapman & Hall / CRC, Boca Raton — London.
Publisher – Googlescholar
18. Windle, A.H. (2007) “Two defining moments: A personal view by Prof. Alan H. Windle,” Composites Science and Technology, 67 (4) 929-930.
Googlescholar
19. Zhang, M. and Li, J. (2009) “Carbon nanotube in different shapes,” Materials Today, 12 (6) 12-18.
Publisher – Googlescholar