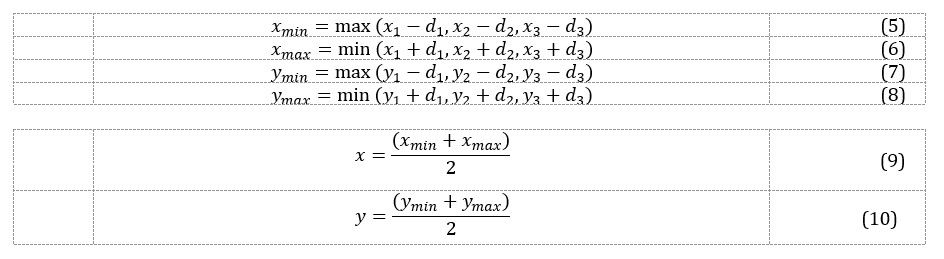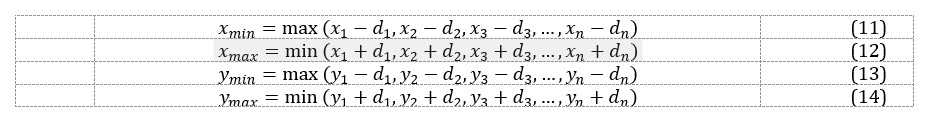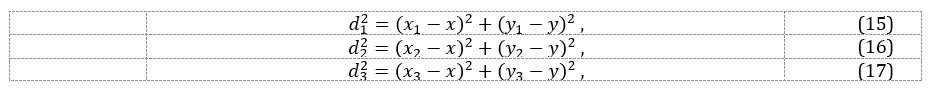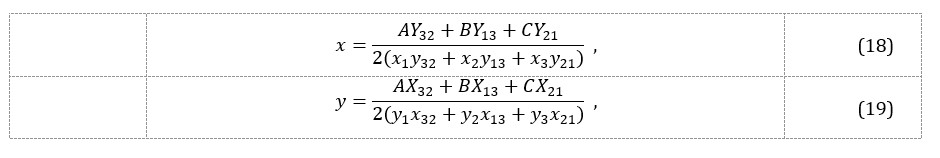Introduction

Unmanned aerial vehicles (UAVs), also known as drones, are increasingly being used in various industries and applications. Here are some areas of the many ways UAVs are being used nowadays:

• Military
• Agriculture
• Surveying and mapping
• Search and rescue
• Construction and infrastructure inspection
• Film and photography
• Delivery and logistics
• Environmental monitoring
• Wildlife conservation

Recently, the use of UAVs for military combat tasks, in particular for reconnaissance and electronic warfare, has become particularly important. The issue of locating the source of radio signal discussed in this article refers to a two-dimensional scenario related to, for example, searching for missing nodes, ensuring radio network connectivity and locating of threats (Michalak J., (2022)) (Michalak J., (2022)). In real application conditions, it is not always possible to use very advanced technical solutions, the increase in precision of which is associated with an increase in weight and financial costs. At the same time, relatively cheap and light UAVs can effectively perform the above-mentioned functions to the satisfaction of the user.

Such a solution in the area of location of radio signal sources by small UAVs (having a simple antenna system and relatively low computing power, based on COTS solutions) is the use of long-known location methods based on the assessment of the distance from the signal source. This assessment is carried out on the basis of the Received Signal Strength Indicator (RSSI).

Localization based on RSSI (together with TOA and TDOA methods) is a method based on distance estimation (Range Based) from the radio signal source (Sivasakthiselvan S., Nagarajan V., (2020)), (Azmi N. A., Samsul S., Yamada Y., Yakub M. F. M, Ismail M. I. M., Dziyauddin R. A., (2018)). It is about a group of methods used in outdoor telecommunications networks. These are: the Min-Max (MM), Least Squares (LS), Trilateration, Maximum Likelihood (ML), ROC-RSSI methods among them (Shi Y., Shi W., Liu X., Xiao X., (2020)).

The accuracy of location of the radio signal source can be increased in these methods (aside from other techniques such as MIMO, diversity or filtering of the received signal) by increasing the number of Reference Points (RP). The use of UAV in this situation seems to be natural.

The article evaluates the proportion of the increase in the accuracy of the location of the signal source in 2D space as a function of the increase in the number of Reference Points and the distance between them. The research was carried out by computer simulation for several selected localization methods based on RSSI in the Rice channel.

Chapter II contains an overview of the related works. Chapters III-V include a description of the simulation model, and Chapter VI presents an analysis of the results.

Related Works

The use of UAVs in the tasks of locating the radio source position is described, for example in (Goswami S., (2013)), (Karimi H. A. Ed, (2016)), (Zekavat S. A., Buehrer R. M. Ed., (2012)), (Liu Y., Yang Z., (2011)), (Poisel R. A., (2012)) (Zafari F., Gkelias A., Leung K. K., (2019)), and localization based on RSSI e.g.in (Uluscan S., Filik T., (2016)), (Saeed N., Nam H., Al-Naffouri T. Y., Alouini M. S., (2019)), (Bohidar S., Behera S., Tripathy C. R., (2015)) and (Duy Q., De P., (2016)). RSSI-based algorithms, although relatively simple, are not usually rated as offering high location accuracy. Such an assessment was presented, for example, in (Azmi N. A., Samsul S., Yamada Y., Yakub M. F. M, Ismail M. I. M., Dziyauddin R. A., (2018)) and (Sivasakthiselvan S., Nagarajan V., (2020)). An analysis of the possibility of increasing the accuracy by using the received signal filtering methods was presented e.g. in (Shi Y., Shi W., Liu X., Xiao X., (2020)).

It is worth emphasizing that localization based on RSSI is cheap and energy efficient.

The method of implementing location algorithms compatible with the Min-Max and Trilateration methods can be found, for example, in (Rattanalert B., Jindamaneepon W., Sengchuai K., (2015)), (Robles J. J., Pola J. S., Lehnert R., (2012)), (Xie S., Hu Y., Wang Y., (2014)) and (Yang K., Liang Z., Liu R., Li W., (2021)). A description of the multi-point location algorithm using the Least Squares solution can be found, for example, in (Guo Z., Xin L., Zhen X., Han L., (2015)) and (Liu L., Ma H., (2014)).

These are, of course, examples of solutions based on RSSI, but it can be assumed that the conclusions of the research results described in this article also apply to the others.

The Network Structure

It is obvious that the effectiveness of a location procedure depends on such factors as the Tracking Base (TB) and the number of Reference Points (RP). Therefore, neither the UAV flight route nor the frequency of measurements is indifferent. For the purposes of the experiment, a route was adopted that guaranteed the achievement of the radio network connectivity (Michalak J., (2021)), (Michalak J., Nowosielski L., (2019)) as shown in Fig 1. The network consists of a certain number of active nodes marked as CH and RN and a localized node UN. The entire network is located on a square area with a side of 1000m, and the UAV flies around the entire area with one of the four turning radii R (see simulation parameters in Table 1).

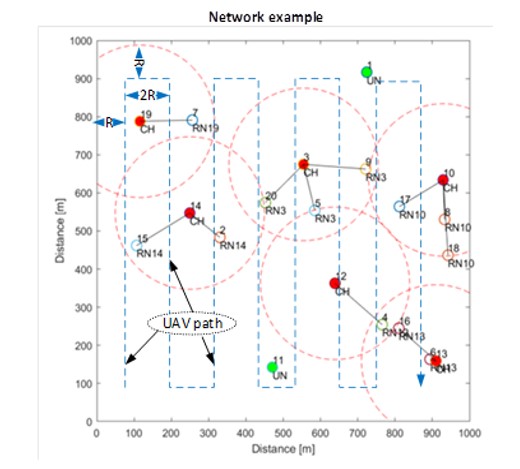
Fig 1. An example of the network structure. RN – Regular Node, CH – Cluster Head (red), UAV – Unmanned Aerial Vehicle (blue line), UN – Unknown Node (green, the localized node)

The basic conditions and assumptions under which the simulation tests were carried out were presented in Fig 2.

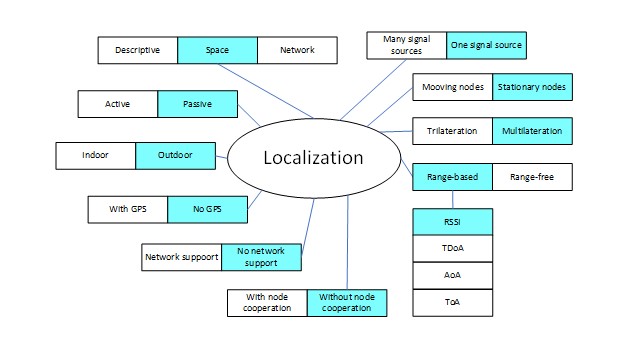Fig 2. Simulation conditions and assumptions

The Radio Channel Model

An overview of radio propagation conditions for UAVs can be found e.g. in (Khawaya W., Guvenc I., Matolak D. W., Fiebig U.C., Schneckenburger N., (2019)). In many cases, a channel of this type can be modeled with a Rice distribution with a  factor value in the range of 7 to 14 (Diang Y., Xiao Y., Xie J., Zhang T., (2017)). We can write the above with the following equations.

1. factor as the ratio of the signal power of the direct path to the sum of the powers of the other (reflected, indirect) paths

For the comparison of the obtained results, the scenario using the FSPL channel and the noise power variance equal to 1 was also used.

Location Methods

Min-Max

The Min-Max method consists in collecting RSSI levels by Reference Nodes (RN) located in positions  where  is a reference to the position number. Each of the RSSI values is converted to the distance from the signal source  (based on the assumed path attenuation equation). Then, for each , squares on the circles of the estimated ranges are determined (Fig.3., (Robles J. J., Pola J. S., Lehnert R., (2012))). It is assumed that the source position is in the center of the common area limited by the values . This can be written in equations 5-8. The center of the common area  is defined by equations 9 and 10.

Fig.3. Illustration of the Min-Max locating concept for 3 Reference Nodes

The generalized form of the Min-Max equations for many points in the 2D plane can therefore be written as: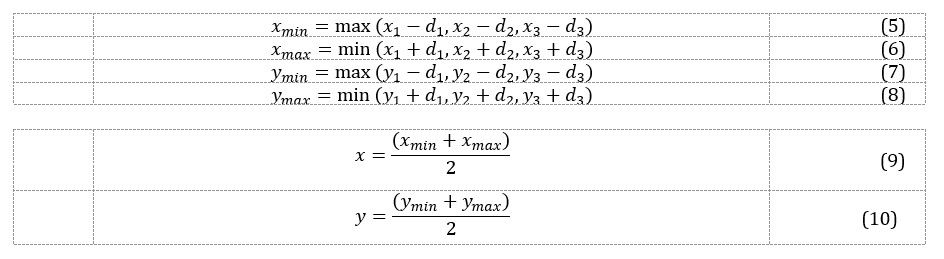

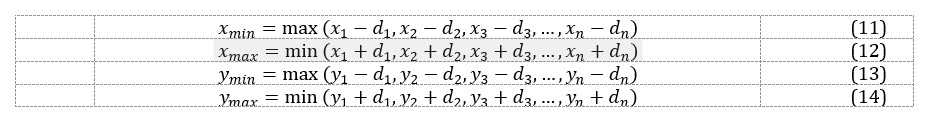
Trilateration

Trilateration, as shown in Fig.4., is based on estimating the distance from the signal source of at least three Reference Nodes with known positions.

Fig 4. An example of trilateration. L (x, y) – position of the localized node

For a two-dimensional scenario, we can write 3 equations in the form:

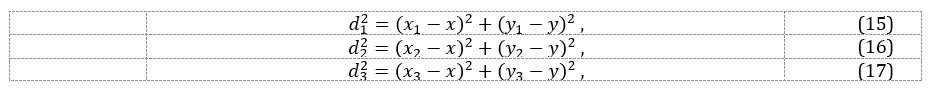
where:

On this basis, the position of the localized node can be determined as:

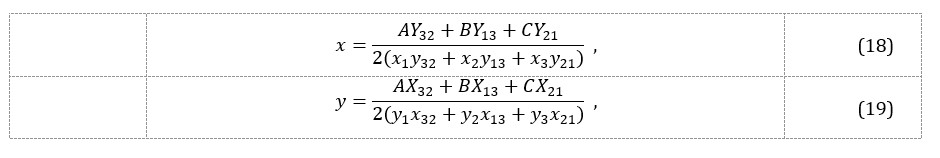
where:

Least-Squares

If the coordinates of the localized node are marked as , and the estimated distances of this node  from the Reference Nodes , , where  is the number of Reference Nodes (UAV measurement points), then we can write (Liu Y., Yang Z., (2011))

 Nonlinear Regression

The Nonlinear Regression (NR) in general is a method of searching for a nonlinear model that describes the relationship between a dependent variable and a set of independent variables. Un like traditional linear regression, which is limited to estimating linear models, Nonlinear Regression can estimate models with arbitrary relation ships between independent and dependent variables. This is achieved using iterative estimation algorithms. To ensure the algorithm works properly, it is important to accurately define the function describing the relationship between the dependent and independent variables, and to correctly select initial values.

In other words, Nonlinear Regression is using a curve or line to create a function that fits an equation to a set of data. The fitness of the regression model is determined by calculating the sum of squares, which is the difference between the mean and each data point. The objective of the model is to minimize the sum of squares using iterative numerical procedures. The principle of least squares is used to obtain the most accurate estimate for the model’s parameters by measuring the number of observations that deviate from the mean of the dataset.

Here, to determine the estimate of the radio signal source location, the MATLAB Nonlinear Regression function was used, giving the model function in the form modelfun = @ (b, X) (abs (b (1) -X (:, 1)). ^ 2 + abs (b (2) – X (:, 2)). ^ 2). ^ (1/2) and the starting point of searching for the optimal solution (position of the target station) in the centre of the monitored plane.

Simulation Results

System Parametrization

The simulations were carried out in the MATLAB R2022b simulation environment (9.13.0.2105380) using the parameters presented in

Table 1.

Table 1: Simulation Parameters

In order to average the test results, each variant of Table 1 was repeated 30 times with different initial parameters of the random generator determining the instantaneous values of each realization of the propagation channel. The averaged absolute value of the signal source location error expressed in meters was evaluated.

Results

Reference Points in FSPL Channel

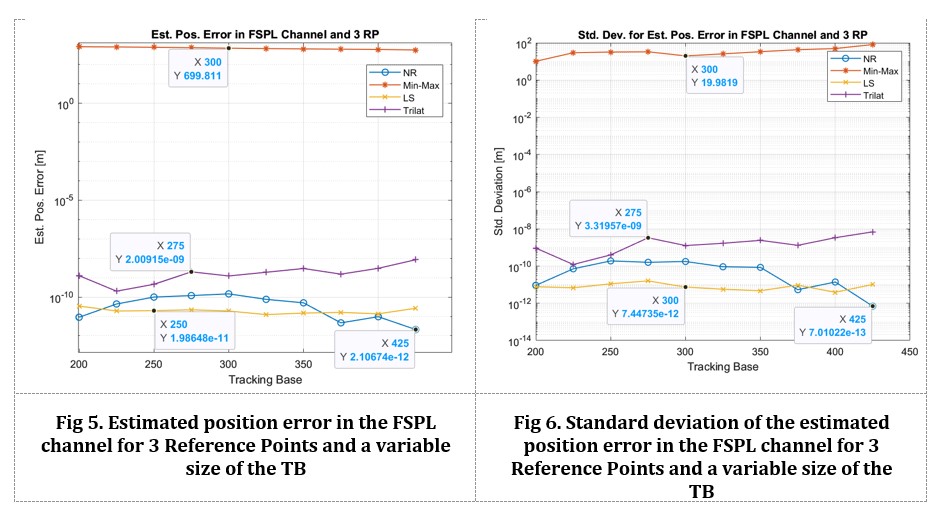
The test is of reference nature and was performed for 3 measurement points and a single channel implementation. Fig.5.and Fig.6. show the estimated position error and standard deviation of the estimated position error as a function of the variable values of the Tracking Base (distances between adjacent measurement points).

It can be seen that 3 Reference Points for the Min-Max method do not give a good result regardless of the dimension of the Tracking Base. At 3 RP, changing the value of Tracking Base (not taking into account very small values) does not significantly affect the accuracy of the location. A significant advantage of the accuracy of LS and NR methods over Trilateration can be noticed. Min-Max method without additional technical measures for the assumed scenario shows relatively large localization errors. More on this can be found in (Robles J. J., Pola J. S., Lehnert R., (2012)).

N Reference Points in FSPL Channel

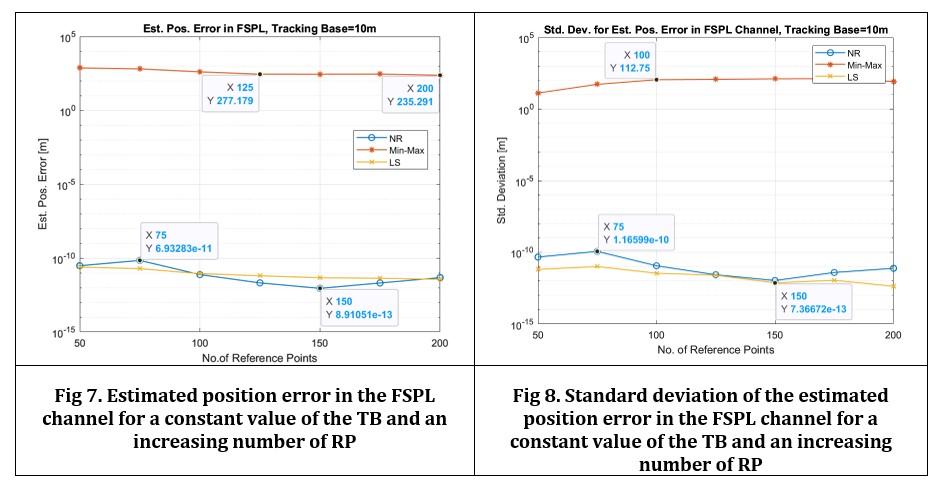
For the increasing number of Reference Points, a significant improvement in the location accuracy can be noticed for the considered methods, excluding Min-Max, for which the improvement in location accuracy is insignificant (Fig 7 and Fig 8.).

 N Reference Points in Rice Channel

Fig 9 and Fig 10show the average results of the evaluation of the location error for a fixed value of the Tracking Base and a variable number of Reference Points in the Rice channel with the coefficient . This time, Kalman filtering of the received signal was also used.

In the Rice channel and  simple tracking methods, the reduction of location errors as a function of the increased number of RP can be observed in each case. For the LS and NR methods, it is about a 10-fold increase in accuracy, which ultimately gives a few dozen meters of location accuracy in a 1000 by 1000m square. Depending on the location method, it is ultimately from 50% (unacceptable) to 2% of the maximum distance of the RP from the signal source (2% at a distance of 1000m gives a 20m

position location error). The use of Kalman filtering gives a several-fold improvement in accuracy for a situation with a small number of RP. This improvement is insignificant with a large number of these points. The Min-Max method does not offer high accuracy. However, it is worth paying attention to the use of the NR function.

 Conclusions

The results of the assessment of the effectiveness of the location of the radio signal source in 2D space, as a function of the growing number of reference points, make it possible to estimate the profits from having a large number of RSSI measurements carried out, for example, with the use of UAVs. It can be seen that with a sufficiently large number of measurements in the Rice channel, the use of filtering of the received signal is no longer significant, and the improvement of the location accuracy is about 10 times. Of course, one should remember the significant influence of changing propagation conditions. It can be assumed that similar results will be obtained in 3D space. However, this is an area for further research.

This work was financed by the Military University of Technology under research project no. UGB/22-860/2023/WAT on “Technologies of modelling and increasing the reliability of ad hoc radio networks”. 

Literature

• Azmi N. A., Samsul S., Yamada Y., Yakub M. F. M, Ismail M. I. M., Dziyauddin R. A., (2018). A Survey of Localization using RSSI and TDoA Techniques in Wireless Sensor Network: System Architecture. International Conference on Telematics and Future Generation Networks, https://doi.org/10.1109/tafgen.2018.8580464.
• Bohidar S., Behera S., Tripathy C. R., (2015). A Comparative View on Received Signal Strength (RSS) Based location Estimation in WSN. IEEE International Conference on Engineering and Technology (ICETECH), March, https://doi.org/10.1109/icetech.2015.7275032.
• Diang Y., Xiao Y., Xie J., Zhang T., (2017). A Time-varying Transition Channel Model for Air-Ground Communication. IEEE Xplore, https://doi.org/10.1109/dasc.2017.8102055.
• Duy Q., De P., (2016). A Survey of Fingerprint-Based Outdoor Localization. IEEE Communications Surveys & Tutarials, https://doi.org/10.1109/comst.2015.2448632.
• Goswami S., (2013). Indoor Location Techniques. Milpitas, : Springer, https://doi.org/10.1007/978-1-4614-1377-6.
• Guo Z., Xin L., Zhen X., Han L., (2015). Weighted Least Square Localization Algorithm Based on RSSI Values. Fifth International Conference on Instrumentation & Measurement, Computer, Communication and Control, https://doi.org/10.1109/imccc.2015.265.
• Karimi H. A. Ed, (2016). Advanced Locatin-Based Technologies od Services. London: CRC Press, https://doi.org/10.1201/b14940.
• Khawaya W., Guvenc I., Matolak D. W., Fiebig U.C., Schneckenburger N., (2019). A Survey of Air-to-Ground Propagation Channel Modeling for Unmanned Aerial Vehicles. IEEE Communicaitons Surveys & Tutorials, https://doi.org/10.1109/comst.2019.2915069, pp. Vol.21, No.3.
• Liu L., Ma H., (2014). Study on Wireless Sensor Network Boundary Localization Based on RSSI. International Conference on Wireless Communication and Sensor Network, https://doi.org/10.1109/wcsn.2014.107.
• Liu Y., Yang Z., (2011). Locatin, Localization and Localizabiility. London: Springer, https://doi.org/10.1007/978-1-4419-7371-9.
• Michalak J., (2021). Efficiency of selected drone flight algorithms in increasing the level of ad-hoc network connectivity without knowing the location of disconnected nodes. International Business Information Management Association (IBIMA), 1-2 April, ISBN: 978-0-9998551-6-4.
• Michalak J., (2022). Location accuracy of a radio ground station in the Rice channel by the multilateration method with the use of non-linear regression function. International Business Information Management Associacion (IBIMA), 30-31 May, ISBN: 978-0-9998551-8-8, ISSN: 2767-9640.
• Michalak J., (2022). Location accuracy of a radio ground station in the Rice channel with the use of signal filtration and non-linear regression function. Conference on Computer Science and Intelligence Systems, 4-7 September, Sofia, https://doi.org/10.15439/2022f15.
• Michalak J., Nowosielski L., (2019). Drone Based Method of Connectivty Assurance for Clustered Network. 23th International Conference Electronics, https://doi.org/10.1109/electronics.2019.8765582.
• Poisel R. A., (2012). Electronic Warfare Target Location Methods. Boston, London: Artech House, ISBN 978-1-60807-523-2.
• Rattanalert B., Jindamaneepon W., Sengchuai K., (2015). Problem Investigation of Min-max Method for RSSI Based Indoor Localization. IEEE, https://doi.org/10.1109/ecticon.2015.7207057.
• Robles J. J., Pola J. S., Lehnert R., (2012). Extended Min-Max Algorithm for Position Estimation in Sensor Networks. IEEE , https://doi.org/10.1109/wpnc.2012.6268737.
• Saeed N., Nam H., Al-Naffouri T. Y., Alouini M. S., (2019). A State-of-the-Art Survey on Multidimensional Scaling-Based Localization Techniques. IEEE Communications Surveys & Tuturials, Vol.21, https://doi.org/10.1109/comst.2019.2921972.
• Shi Y., Shi W., Liu X., Xiao X., (2020). An RSSI Classification and Tracing Algorithm to Improve Trilateration-Based Positioning. Sensors, 30 July, https://doi.org/10.3390/s20154244.
• Sivasakthiselvan S., Nagarajan V., (2020). Localization Techniques of Wireless Sensor Networks: A Review. International Conference on Communication and Signal Processing, 28-30 July, https://doi.org/10.1109/iccsp48568.2020.9182290.
• Uluscan S., Filik T., (2016). A Survey on the Fundamentals of RSS based Localization. https://doi.org/10.1109/siu.2016.7496069.
• Xie S., Hu Y., Wang Y., (2014). An Improved E-Min-Max Localization Algorithm in Wireless Sensor Networks. IEEE, https://doi.org/10.1109/icce-china.2014.7029851.
• Yang K., Liang Z., Liu R., Li W., (2021). RSS-Based Indoor Localization Using Min-Max Algorithm With Area Partition Strategy. IEEE Access, 17 September, https://doi.org/10.1109/access.2021.3111650, p. vol. 9.
• Zafari F., Gkelias A., Leung K. K., (2019). A Survey of Indoor Localization Systems and Technologies. IEEE Communications Surveys & Tuturials, https://doi.org/10.1109/comst.2019.2911558.
• Zekavat S. A., Buehrer R. M. Ed., (2012). Handbook of Position Location. Hoboken: Wiley, https://doi.org/10.1002/9781118104750.