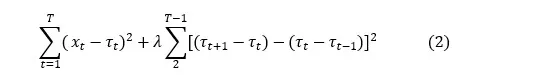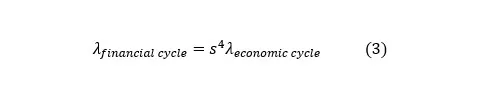Introduction
The study of the financial system in the macroeconomic context experienced a revival after the Great Financial Crisis (GFC) which debuted in 2007. The effects of the crisis were so strong and unforeseen that they required an update of the existing way of thinking in order to capture the phenomena experienced during the crisis. At the same time, the GFC also demonstrated the need for financial system-specific stabilizing tools to ensure greater resilience to shocks. This gave rise to the concept of macroprudential policy and its specific instruments, widely adopted worldwide notably through the Basel agreements. In Europe, the coordination of macroprudential policy falls under the remit of national authorities, state cooperation being achieved through the forums of the European Systemic Risk Board (ESRB).
In Romania, macroprudential policy is ensured by the National Committee for Macroprudential Oversight (NCMO), an authority which is composed of members of the National Bank of Romania (NBR), the Financial Supervisory Authority and the Government through the Ministry of Finance. The main macroprudential tools that can be used by the NCMO consist of capital buffers, which represent additional capital requirements for Romanian banks to allow for better loss absorption in case of the manifestation of structural and cyclical risks identified in the Romanian economy. Since its inception, the NCMO has activated several capital-based measures that required banks to hold higher levels of capital in respect to their Risk Weighted Assets. The latest value of the capital buffers is the following (NCMO 2024): a Systemic Risk Buffer (SyRB) which takes the value of 0%,1% or 2%, an Other Systemically Important Institution Buffer (O-SII) which is calibrated in the interval 0.5%-2%, and a Countercyclical Capital Buffer (CCyB), calibrated since 2023 at 1% level.
Modeling the impact of a change in macroprudential policy by setting a different level of capital buffers requires a macroeconomic model that also incorporates a financial system. Such models started to be developed in particular in the 1990s, a canonical model from that period being summarized in Bernanke (1999). The main result obtained is given by the presence of a financial intermediation activity that has the potential to accentuate the business cycle, this mechanism known as the financial accelerator.
Given the complexity of the interaction between the financial system and the real economy, it has not been possible to fully model financial phenomena. Thus, macro-prudential policy-makers rely on several models, each with its own specificities, to take macroprudential policy decisions. Banque de France (Bennani et al., 2017) admits the use of two Dynamic Stochastic General Equilibrium (DSGE) models, namely Gerali et al. (2010) and Mendicino et al. (2018), along with a macroprudential stress-testing model. The German Bundesbank also employs the use of at least two DSGE models for the same purposes: Gerali et al (2010) and Hristov and Hulsewig (2017). The European Central Bank (Cozzi et al 2020) uses four DSGE models in analyzing macroprudential decisions: Darracq-Paries et al (2011), Darracq-Paries et al (2016), Mendicino et al (2018) and Coenen et al (2018).
When faced with the decision of imposing higher capital-based requirements through the use of macroprudential policy instruments, the policy makers will be in a better position if they hold evidence of what effects their actions would have on the overall economy. DSGE models with a complex representation of the financial sector are a proper way to answer such inquiries. However, most of the models that incorporated macroprudential policy have so far been estimated and calibrated for the large economies of the euro zone. By adapting such a model to the Romanian economy, our study would provide evidence as to the transmission of the macroprudential policy in a smaller economy, with a less complex financial system.
Model
The model is based on the framework outlined in Gerali et al (2010), while also including some modifications required to better grasp the scope of the paper. The original model was designed to study the impact that the banking sector had in the GFC, but the fact that it contains a parameter that determines the capital requirement of banks makes it a perfect candidate in order to analyze the effects of an increase in capital buffers for banks. The model incorporates a monopolistic banking sector, borrowers with collateral constraints on borrowing, and other nominal frictions. Financial intermediation is imperfect because banks have an adjustment cost each time their capital level differs from an exogenous target level, and the additional costs are passed on to customers through higher interest rates. Banks adjust equity capital at a slow rate by retaining earnings. There is also no direct funding and all transactions are intermediated by the banking sector.
The economy is populated by three types of agents – patient households, impatient households, and entrepreneurs – who maximize their utilities subject to their respective resource constraints. Both types of households work, consume and save/borrow and own real estate. The last class of agents, entrepreneurs, consume, borrow, and combine labor and capital through a Cobb-Douglas function with a productivity variable to produce a homogeneous good that is further differentiated and sold as a final consumption good. Households and entrepreneurs differ in intertemporal discount factors. The model allows the study of supply-side shocks in the credit market. There is a continuum of identical banks consisting of three branches: the wholesale branch and two retail branches, one for lending and one for deposits. Each perfectly competitive banking group distributes loans to impatient households and entrepreneurs and raises funds by collecting deposits from patient households or by incorporating capital, subject to an accounting balance sheet constraint. The two retail branches, namely the deposit branch and the lending branch, operate under monopolistic competition and set interest rates on deposits and loans in relation to their respective elasticities of substitution. Each wholesale branch acts as a link between the two retail branches and combines bank capital and deposits for lending. The bank’s equity capital is accumulated only through retained earnings. Given that deposit or equity financing are perfectly substitutable, each bank’s choice is given by the capital requirement target parameter from which deviation is costly. Monetary policy is introduced by a standard Taylor rule that sets the interbank market interest rate. Individual workers offer slightly differentiated types of labor, so they must be aggregated by perfectly competitive unions. Unions set the nominal wage of each individual worker by maximizing the utility derived from the wage received relative to the hours worked and is subject to adjustment costs and price rigidity. Retailers, represented by patient households, are monopolistically competitive and buy only the wholesale good produced by entrepreneurs at a producer price before selling it slightly differentiated at a final price. Producers of capital goods buy the capital left over after production, repurpose those units of capital through investment and sell the new productive capital back to the entrepreneurs at the end of the period.
In the original model, the supply of real estate is fixed. In our adaptation, we introduce a sector of real estate producers owned by patient households, following the example of Bennani et al. (2017). In a similar way to capital goods’ producers, they buy the remaining non-depreciated real estate after consumption and recomplete those real estate units through investment, then sell the new units back to households at the end of the period. The introduction of this sector gives a higher degree of flexibility to the model and also allows for the study of the impact of shocks on the housing market, which is important for the conduct of macroprudential policy. The final output on the economy is given by the sum of total consumption of the households and entrepreneurs, the total investment in capital and housing. The model is log-linearized around the steady states.
The key equation for studying the effect of macroprudential policy is the one that defines how the loans are priced. The equation below shows that the spread between the wholesale loan rate and the monetary policy rate is equal to the cost, computed through a parameter , of deviating with the capital ratio (given by the ratio of banking capital to total loans ) from the target . The cost of deviating is symmetrical, upward deviation is similar to downward deviation.

In the original model, the parameter is fixed. In order to introduce a shock to macroprudential policy based on capital requirements, it is necessary to endogenize the parameter . In this regard, we have taken two approaches. Firstly, was considered to follow a simple process, varying tightly ( being close to 0) around a steady state with an exogenous shock that follows a normal process.
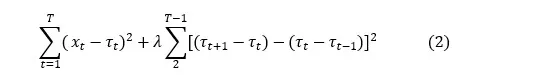
Following this approach, the interpretation is that the macroprudential authority imposes a steady state capital target that banks must keep close to. The capital target thus chosen is no longer a strict minimum requirement, but a strong guidance provided by the authorities to banks as to the level of capital that banks should hold. This target can be shocked in the short term, which corresponds to the need to temporarily maintain a higher capital requirement, similar to the objective of the countercyclical capital buffer instrument. In addition, the policymakers may increase the steady state level of the target, which is associated with a permanent capital requirement shock, similar to the adoption of a capital buffer for structural risk (the systemic risk buffer).
Our second approach in endogenizing the parameter follows the method presented in Bennani et al (2017), with the introduction of a new term to the equation above. The new addition increases the capital target when the current credit-to-GDP, given by loans to impatient households and entrepeneurs and output , is larger than its long term ratio. This rule corresponds to the current guidance in calibrating the counter-cyclical capital buffer (CCyB) based on the deviation of credit-to-GDP from its trend (ESRB 2014). The parameter is calibrated at 0.25, so that a 10% deviation is associated to a 2.5 p.p. increase in the capital target. The rule can also act in the inverse way, decreasing the capital requirements when the deviation is negative. Thus, it can act as an automatic stabilization mechanism of the financial cycle.
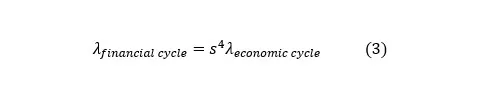
Estimation and Calibration
The model contains both calibrated and estimated parameters. Some of the parameters are calibrated according to empirical evidence in the literature on their level for the Romanian economy (discount rate for patient households, inverse of the Frisch elasticity, proportion of patient households, capital utilization as a function of output, capital depreciation rate, LTV for households), while other parameters are set to correspond to certain observed moments in the data (e.g., elasticities of borrowing and saving). The level for has been calibrated at 16%, corresponding to an average level that a Romanian bank can have using current regulations (formed by taking 8% minimum Pillar 1 requirement + Pillar 2 requirements + 2.5% Capital Conservation Buffer + SyRB+ OSII Buffer +1% CCyB + Management Buffer). Some parameters are retained at the same value as in the original article as no other source of information could be found that points to a different value. Table 1 summarizes the values of the calibrated parameters.
Table 1. Calibrated parameters values
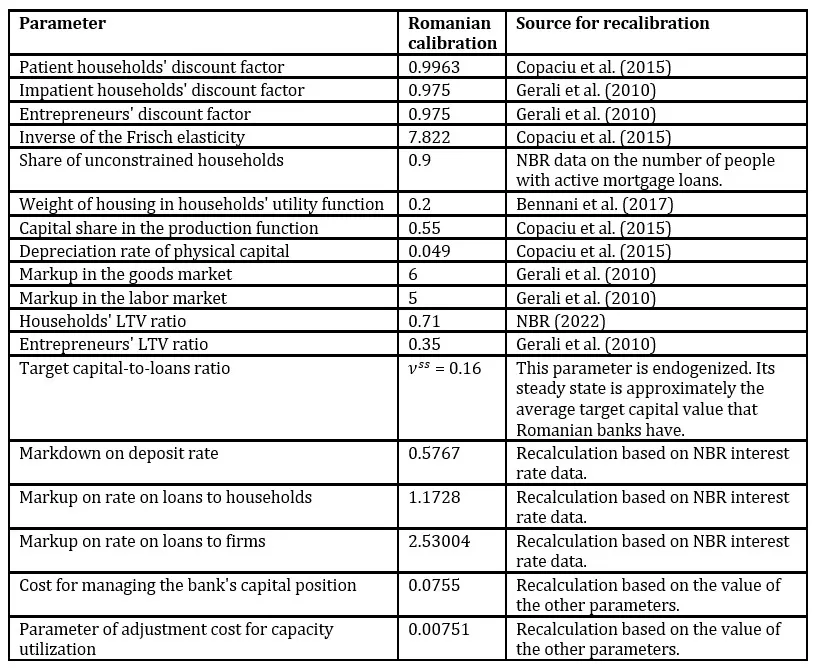
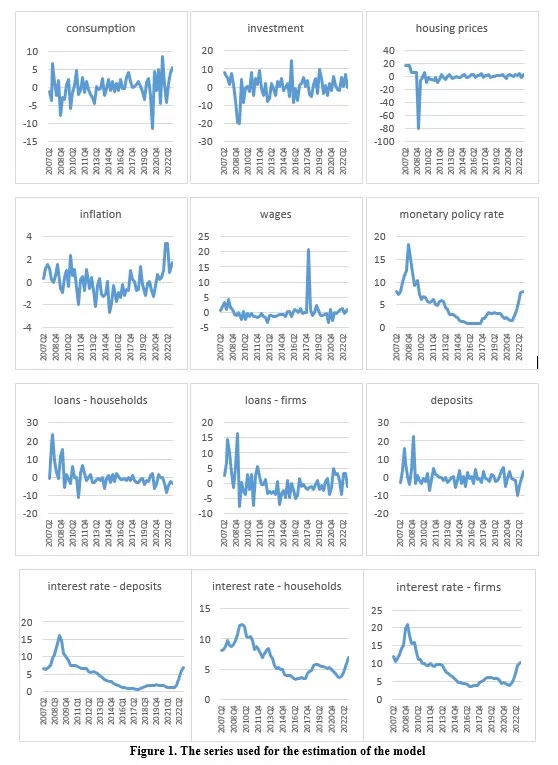
The remaining parameters are estimated using Bayesian techniques, based on the Metropolis Hastings algorithm with 10 chains, each with 100,000 draws using the Dynare software. Each parameter is assigned a distribution type on the basis of a priori, generally uninformative values. The priors and the distributions were maintained the same as in Gerali et al. (2010), or as in Bennani et al. (2017) for the additional parameters. The posterior values of the parameters are estimated based on 12 data series: consumption, investment, real estate prices, inflation, wage growth, household credit, non-financial corporates credit, household deposits, interbank interest rate, interest rate on housing loans, interest rate on non-financial corporate loans and interest rate on household deposits.
In order to estimate the model for the Romanian economy, quarterly data from the Q1 2007 – Q4 2022 time interval were used. Final consumption expenditure of household and gross fixed capital formation data series were downloaded from Eurostat, seasonally and calendar adjusted, and divided by the GDP deflator, as suggested in Pfeifer (2014). The index published by the Romanian National Statistical Office was used for the change in real estate prices. Quarterly inflation was determined on the basis of the HICP index extracted from Eurostat. Wage growth has been determined on the basis of the index reported on Eurostat for quarterly seasonally and calendar adjusted quarterly wage growth for all basic economic sectors. Credit and deposit volumes were extracted from the NBR’s public database and deflated by the GDP deflator. The interbank interest rate used is ROBOR 3M taken from the NBR’s website. Interest rates on loans and deposits were determined as quarterly averages of the interest rates on the volume of new loans in RON, all series being taken from the NBR’s public database. The series used for the estimation of the model are pictured in Figure 1.
Results
A general feature of the recalibration and reestimation of the model for Romania, compared to the original article that is calibrated for the euro area economy, is the much lower persistence of shocks, most of which are neutralized within a maximum of 2 years, while in the original model the time period over which the variables are affected is much longer. However, the low persistence is compensated by a much larger amplitude in the main variables’ response to shocks.
A macroprudential policy shock given by an increase in the capital target by one standard deviation leads to an increase in bank capital and an increase in interest rates, resulting in a decrease in the volume of lending (Figure 2). Patient households use deposits to purchase real estate, taking advantage of falling real estate prices. They also take advantage of the higher profits of banks, which are attributed to them through dividends. Investment in housing production falls sharply, leading to a decrease in housing prices in the medium term. Thus, capital based macroprudential policy is effective in countering a bubble in the housing market. Impatient households, on the other hand, are hit hard by the shock, effectively blocking access to finance by increasing costs. The same is true for firms, but they overcome the shock much more quickly, resuming borrowing for capital relatively quickly. On the impact of the shock, consumption and investment fall, leading to a fall in output, but the shock is quickly absorbed and the effects for output disappear after 3 quarters.
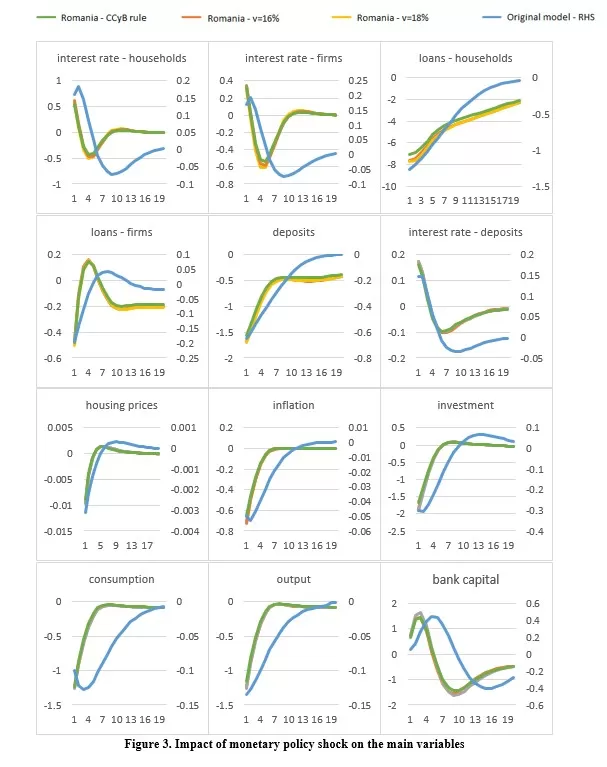
In the case of a monetary policy shock, the main variables have a similar behavior to a macroprudential policy shock, owing to the common transmission mechanism that both policies share (Figure 3). However, the monetary policy shock effects lead to a much greater amplitude in the decrease of investment, consumption and output, and the variables return to steady state after longer time. This leads to the idea that monetary policy “gets in all the cracks” of the economy, and is much more effective in stabilizing a heating economy. Although it is effective in lowering inflation, at the cost of lower output, interestingly, real estate output increases, again due to patient households purchasing real estate. Thus, addressing a housing construction bubble just through monetary policy is not effective.
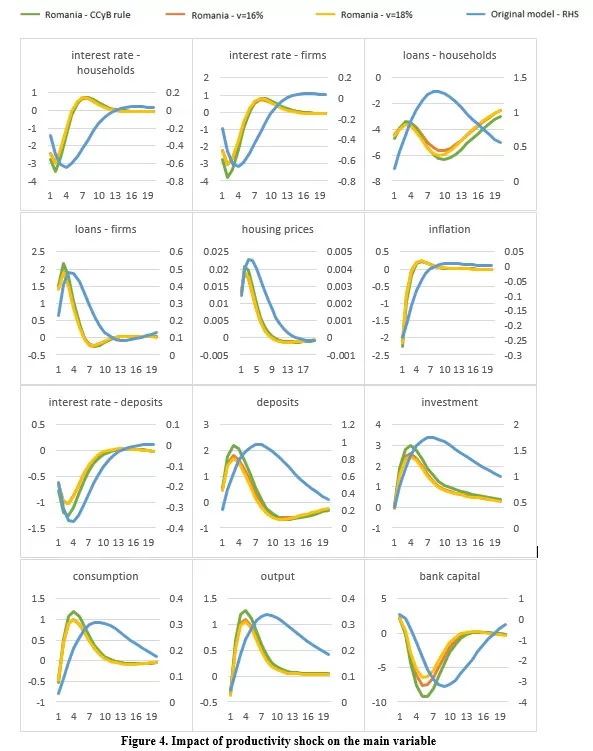
Analyzing the impact of a productivity shock, the positive impact on consumption, investment, and output stands out (Figure 4). The productivity shock is defined as a positive increase in the productivity variable that affects the production of consumption goods by the entrepreneurs, thus increasing the efficiency through which the labour and capital are purposed. Following this shock, interest rates fall, leading to an increase in corporate lending. Bank capital falls as lending is financed by new household deposits. Overall inflation falls, but house prices increase due to the boom in production output of real estate. Paradoxically, even in this case, impatient households fail to accumulate more real estate, as lending to them falls.
The final shock study case is one to the bank’s capital, similar to a situation of increasing losses to the credit portfolio (Figure 5). The fall in bank capital is associated with an increase in interest rates, as the capital requirement is binding and the bank no longer has sufficient funds to meet it, thus lending stalls. Transfers from bank profits cause patient households to consume more and accumulate real estate, with the production of real estate increasing. Impatient households find the resources to consume in the short run by giving up housing assets, but long-term consumption falls. The hardest hit are entrepreneurs, whose both consumption and capital holdings fall. Overall, the economy is suffering, slipping into recession. The capital requirement target adjusts, first decreasing to accommodate the shock, then increasing to cause banks to reach the steady state level.
In the approach in which capital requirements follow a macroprudential policy rule, the form of the impulse-response functions is not affected across the 4 shocks studied. However, the amplitude of the response to the shocks differs than in the calibration with a simpler capital target rule. The use of a CCyB rule manages to minimize the impact on the economy in the case of macroprudential policy and monetary policy shocks, but even more so in the scenario where a negative shock to bank capital occurs. However, in the case of the productivity shock, the amplitude of the variable responses is larger than in the other cases.
In another experiment, we increased the steady state values of the capital target parameter from 16% to 18% in the simple endogenization of the parameter. Following this recalibration, we can simulate the impact of an increase in the structural part of the capital target. Although having similar shapes, the amplitude of some of the shocks’ responses is larger in this experiment. In the case of the macroprudential policy shock, the house prices’ correction is greater. Moreover, in the case of a productivity shock, the bank capital is less depleted but the impact of output is also smaller. Finally, the greater capital target amplifies the effects of the bank capital shock, as the costs of adjusting to the higher requirement is larger.
Conclusion
In this article, we have showed how macroprudential policy can be used by policy makers to achieve certain macroeconomic objectives. The introduction of capital-based macroprudential policy instruments can be effective in cooling an overheating economy as it temporarily brings down investment, consumption and output. Moreover, a capital target increase can help in bursting a real estate price bubble on the medium-term perspective. However, compared to a monetary policy shock, macroprudential policy is not as effective at achieving sharp macroeconomic stabilization, as its effects are smaller and more short-lived. Furthermore, having in place a higher capital requirement for banks can dampen the effects of a productivity shock, and amplify the effects of a bank capital shock. Finally, by comparing the results of the Romanian calibration to the euro area calibration used in the original Gerali et al. (2010) model, it can be concluded that the shocks to the smaller economy are greater in amplitude but have shorter-lived effects.
A caveat of the analysis is that the capital target requirement assumes that banks operate exactly at the target required, incurring additional costs if deviating upwards or downwards from the target. In reality, banks maintain significant management buffers, in order to make sure they don’t breach the capital requirements. The adjustment costs for deviating are not symmetrical as in the model, but are much more stringent in case of a downward breach that can bring regulatory actions by the supervisors.
As stated in the introduction, a modelling feature that has gained traction in the macroprudential policy domain are DSGE models with agent default, introduced in Mendicino et al. (2018). A future avenue of research would be to calibrate such a model for the Romanian economy and see how the results differ from the ones presented in this paper. Moreover, as the heterogenous agent model literature is expanding, future studies can incorporate macroprudential policy into such a model and analyze the differences to the representative agent-based models.



Bibliography
- Bennani, T., Couaillier, C., Devulder, A., Gabrieli, S., Idier, J., Lopez, P., Piquard, T. and Scalone, V. (2017) ‘An analytical framework to calibrate macroprudential policy.’ Banque de France Working Paper, 648.
- Bernanke, B. (1999) ‘The financial accelerator in a quantitative business cycle framework,’ Handbook of Macroeconomics, Elsevier.
- Coenen, G., Karadi, P., Schmidt, S. and Warne, A. (2018) ‘The new area-wide model II: an extended version of the ECB’s micro-founded model for forecasting and policy analysis with a financial sector.’ ECB Working Paper, no. 2200.
- Copaciu, M., Nalban, V. and Bulete, C. (2015) ‘REM 2.0, an estimated DSGE model for Romania,’ 11th Dynare Conference, National Bank of Belgium, Brussels.
- Cozzi, G., Darracq Paries, M., Karadi, P., Körner, J., Kok Sørensen, C., Mazelis, F., Nikolov, K., Rancoita, E., Van der Ghote, A. and Weber, J. (2020) ‘Macroprudential policy measures: macroeconomic impact and interaction with monetary policy,’ ECB Working Paper, no. 2376.
- Darracq Pariès, M., Jacquinot, P. and Papadopoulou, N. (2016) ‘Parsing financial fragmentation in the euro area: a multi-country DSGE perspective.’ ECB Working Paper, no. 1891.
- Darracq Pariès, M., Kok, C. and Rodriguez-Palenzuela, D. (2010) ‘Macroeconomic propagation under different regulatory regimes: evidence from an estimated DSGE model for the euro area.’ ECB Working Paper, no. 1891.
- European Systemic Risk Board (2014) ‘ESRB handbook on operationalizing macro-prudential policy in the banking sector.’
- Gerali, A., Neri, S., Sessa, L. and Signoretti, F.M. (2010) ‘Credit and banking in a DSGE model of the euro area,’ Journal of Money, Credit and Banking, vol. 42, pp. 107-141.
- Hristov, N. and Hülsewig, O. (2017) ‘Unexpected loan losses and bank capital in an estimated DSGE model of the euro area,’ Journal of Macroeconomics, vol. 54, pp. 161-186.
- Mendicino, C., Nikolov, K., Suarez, J. and Supera, D. (2018) ‘Optimal dynamic capital requirements,’ Journal of Money, Credit and Banking, vol. 50(6), pp. 1271-1297.
- National Bank of Romania (2022), ‘Financial stability report 2022.’
- National Committee for Macroprudential Oversight (2024), ‘Annual report 2024.’
- Pfeifer, J. (2014) ‘A guide to specifying observation equations for the estimation of DSGE models,’ Research series, pp. 1-150.