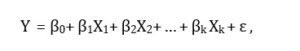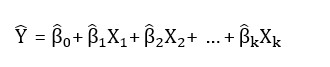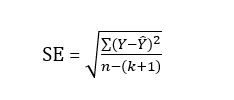A Machine Learning Approach to Identify Impact of Mathematical Courses Performance in Engineering Degree Program

Introduction

Mathematics and Basic Science are an integral part of any engineering degree program. Mathematical technique models and reasoning are integral to most areas of engineering and the discipline depends on mathematics for many of its fundamental underpinnings [ACM (IEEE) CE. 2016]. Science provides us with the laws of the natural world and Mathematics helps us establish relationships among different components [1]. Mathematics is comprehensively used in Physics, structurally in graphics and practically in engineering. Mathematical courses play a key role in the understanding and application of engineering programs. Enhancing student’s academic enactment via Mathematical courses is one of the prime services of the academic community of higher education. Mathematical courses can develop intellectual maturity. Engineers use Mathematics as a tool for solving numerous boundary value problems and optimization problems. According to the information by United States National Research Council (1989), simple skills of Mathematics and geometry are essential for almost all occupations. Tobias (1978) emphasized the importance of basic high school mathematics knowledge in the examinations required for recruitment in the public and private sectors.

Mathematics provides a language for working with ideas relevant to computer engineering, specific tools for analysis and verification, and a theoretical framework for understanding important ideas [ACM (IEEE) CE2016]. Mathematics and science courses are considered for creating an overall style or ethos for a specific computer engineering degree program. [ACM (IEEE) CE. 2016]

The article presents a multiple linear regression model to analyze the student’s final grade (CGPA) based on his/her grade in four Mathematical courses, namely Calculus I, Calculus II, Linear algebra and Differential equations, in an Engineering degree program. In the first level of Calculus, students get knowledge about limits, continuity, derivative and integration with application. In the second level of Calculus, the concept of Improper integral, functions of several variables, Multiple Integral, Polar curves, Sequence and Series are introduced to the students. In the Linear Algebra course students learn Matrices and Determinant with applications, Eigenvalues and Eigen vectors, Analytic functions etc. The calculus and differential equations are required to support engineering materials such as communications theory, signals and systems, and analog electronics. The analysis of continuous functions is fundamental to all engineering programs [ACM IEEE CE. 2016]. Linear algebra is required for solving networks of equations describing voltage/current relationships in basic circuits and is used in engineering application areas such as computer graphics and robotics [ACM IEEE CE. 2016].

In this paper, multiple regression analysis has been used as a technique to visualize the influence of Mathematical courses on the final grade of an engineering student. Multiple Regression is a set of techniques used to analyze the relationship between two or more independent variables and a dependent variable. Multiple linear regression is defined as a multivariate technique for determining the correlation between a response variable Y and a combination of two or more predictor variables, X, Montgomery and Peck, 1982; Draper and Smith, 1998; Tamhane and Dunlop, 2000; and McClave and Sincich, 2006. It can be used to analyze data from causal-comparative, correlational, or experimental research.

Multiple linear regression is one of the most widely used statistical techniques in the educational research. It is regarded as the “Mother of All Statistical Techniques”. Many colleges and universities develop regression models for predicting the GPA of incoming freshmen. The predicted GPA can then be used to make admission decisions. In addition, many researchers have studied the use of multiple linear regression in the field of educational research. The use of multiple linear regression has been studied by Shepard (1979) to determine the predictive validity of the California Entry Level Test (ELT). In a research by Draper and Smith 1998, the use of multiple linear regression is illustrated in a prediction study of the candidate’s aggregate performance in the G. C. E. examination.

A multiple linear regression model based on a number of independent (or predictor) variables X, X₁, …, X_k can be obtained by the method of least squares, and is presented by the following equation

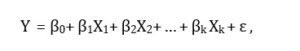
where Y = response variable, X =predictor variables, β_k = the population regression coefficients, and ε = a random error, (Mendenhall et al., 1993; and Draper and Smith, 1998). Multiple linear regression allows for the simultaneous use of several independent (or predictor) variables, X, to explain the variation in the response variable Y. The fitted equation is presented as follows:

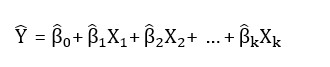
where  = predicted or fitted value and  = estimates of the population regression coefficients.

Multiple standard error of estimate measures the error in the predicted value of the dependent variable. 

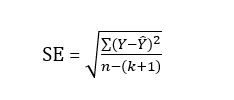
Where:

Y is the observation.

 Y is the value estimated from the regression equation.

n is the number of observations in the sample.

k is the number of independent variables.

SE is the standard error of estimate.

Methodology

In this resourceful experimental study, the inference of Mathematical courses over the CGPA of a student in an engineering degree program was observed. In this study, marks obtained by 36 students in four different mathematical courses and their CGPA have been analyzed via multiple regression method. , as shown in Table 1.

Table 1: Marks and CGPA of students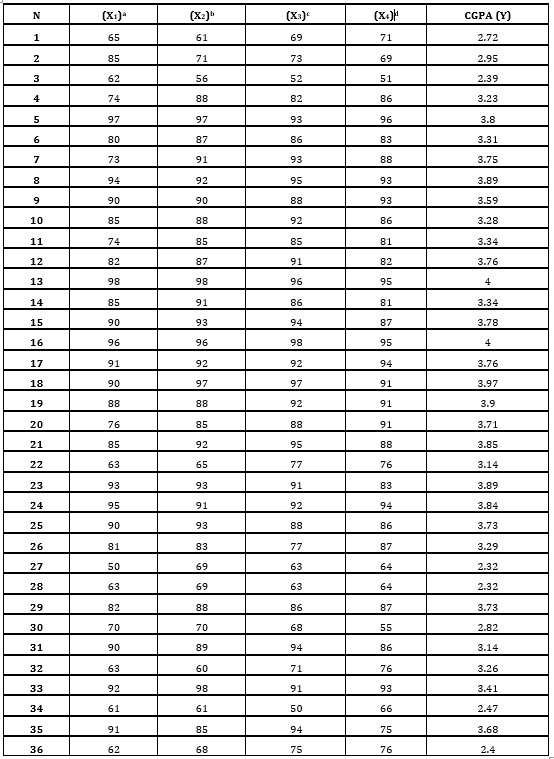

^a: Calculus I

^b:  Calculus II

^c: Linear Algebra

^d: Differential Equations

The objective of this study is to develop an appropriate multiple linear regression model to relate the student’s CGPA (considered as the dependent or response variable Y) to the student’s scores in four Mathematical courses (considered as the independent or predictor variables X). It examines how well the scores in mathematical courses could be used to predict the student’s GPA.

This study investigates the feasibility of the use of the four constraints, namely X_1, X₂, X₃ and X₄ for 36

undergraduate students enrolled in an engineering degree program in 4 mathematical courses. The multiple regression method is used to analyze the result. The following model was developed to find the expected CGPA.                                                   

Table 2 shows the Regression statistics obtained from the data, and Table 3 shows the standard error (SE) and regression coefficients.

Table 2: Regression Statistics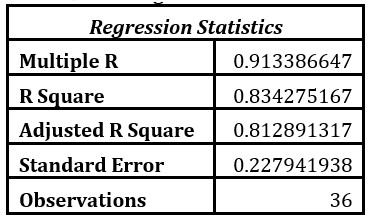

Table 3: Statistical Data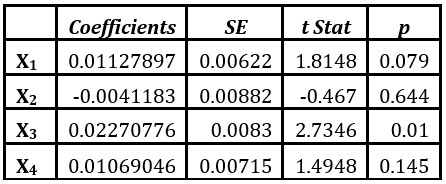

Table 4: Analysis of Variance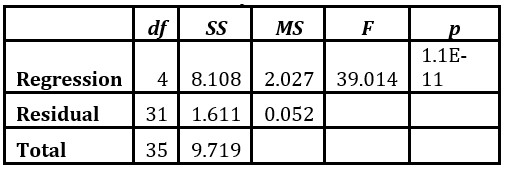

 Interpretation of the Results

1. From the analysis of the variance table, it is observed that the p-value is very small 1E-11. This implies that the model estimated by the regression procedure is significant at an α -level of 0.05. Thus at least one of the regression coefficients is different from zero.
2. The p-values for the estimated coefficients of X₁ and X₃ are 079 and 0.01, respectively, indicating that they are significantly related to Y. The p-value for X₂ is 0.644, indicating that it is probably not related to Y and the p-value for X₄ is 0.0145, indicating that it is less related to Y at an α -level of 0.05.
3. The R² value in the regression output indicates that only 4 % of the total variation of the Y values in terms of their mean can be explained by the predictor variables used in the model. The adjusted R² value indicates that 81.3% of the total variation of the Y values in terms of their mean can be explained by the predictor variables used in the model. As the values of R² and adjusted R² are not very different, at least one of the predictor variables contributes to the prediction of Y.  
4. The variance of the regression of the dependent variables for any given set of the independent variables is estimated by the residual mean square (s²) which is equal to ss(residual) divided by an appropriate number of degrees of For this problem, s² = 0.051968 and s = 0.22796.

Since the ‘s’ value is very small, it indicates that the prediction is meticulous.

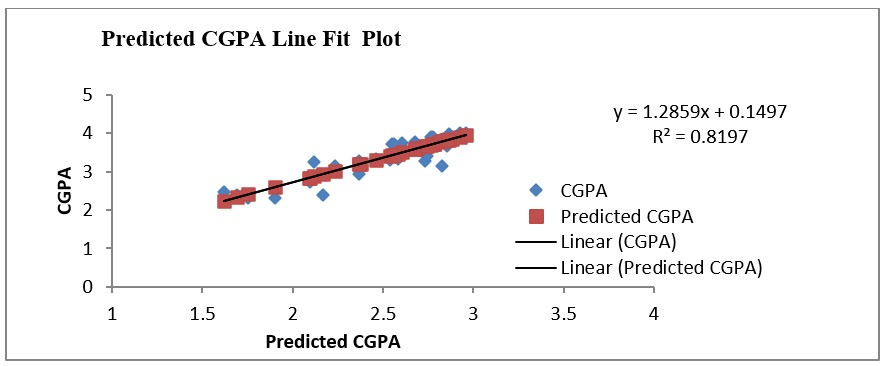Figure 1

Figure 1 shows the regression plot of CGPA versus predicted CGPA. The R value for this plot is 0.905387 which indicates that the CGPA and  the Predicted CGPA are strongly related. The R² value in this plot is 0.8197 which shows that the regression predictions fit decisively.

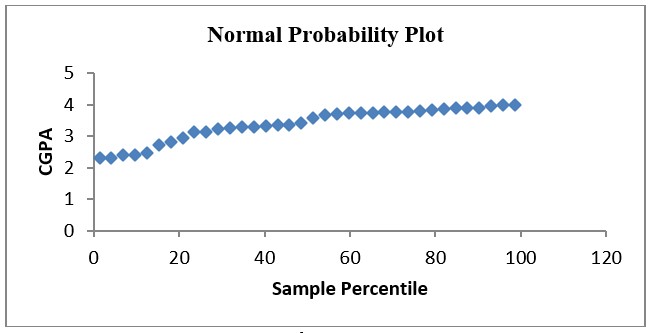
Figure 2

Figure 2 shows the Normal probability plot. From the plot, it is observed that there exists an approximately linear pattern. This indicates the consistency of the data with a normal distribution.

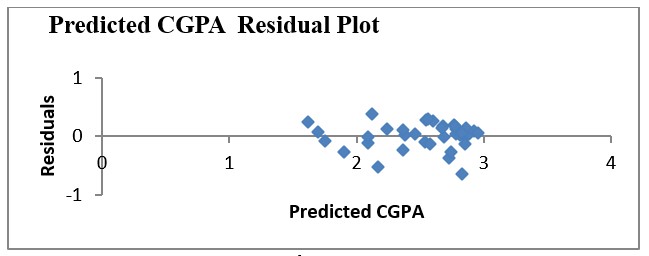
Figure 3

Figure 3 provides the predicted CGPA residual plot.

A residual plot is a graph that shows the residuals on the vertical axis and the independent variable on the horizontal axis. If the points in a residual plot are randomly dispersed around the horizontal axis, a linear regression model is appropriate for the data; otherwise, a non-linear model is more suitable [2]. This plot shows a random pattern which is a good fit for the linear model.

Conclusion

From the above analysis, it appears that the multiple regression model for predicting the student’s CGPA is useful and adequate. The ‘s’ value in the given study is very small which implies that at least one of the predictor variables contributes to the prediction of CGPA.

References

• Bianchi F, Stobbe K, Eva K (2008), Comparing academic performance of medical students in distributed learning sites. The McMaster experience. Medical Teacher (30), 67-71
• Borg, R., and Gall M. D. (1983). Educational Research – An Introduction (4^th edition). New York & London: Longman.
• Draper, R., and Harry S. (1998). Applied Regression Analysis (3rd edition).
• New York: John Wiley & Sons,
• Mendenhall, , James E. R., and Robert J. B. (1993). Statistics for Management and Economics (7th edition). Belmont, CA: Duxbury Press.
• Montgomery D.C. (1997) Design and Analysis of Experiments, 4th ed. Wi1ey, New York
• Montgomery, C., and Peck, E. A. (1982). Introduction to Linear Regression Analysis. New York: John Wiley & Sons, INC.
• Senfeld, (1995). “Math anxiety and its relationship to selected student attitudes and beliefs,” Ph. D. Thesis. Coral Gables, Florida: University of Miami.
• Shakil, (2001). “Fitting of a linear model to predict the college GPA of matriculating freshmen based on their college entrance verbal and mathematics test scores,” A Data Analysis I Computer Project. University Park, Florida: Department of Statistics, Florida International University.
• Tamhane, C., and Dunlop, D. D. (2000). Statistics and Data Analysis: From Elementary to Intermediate (1st edition). Upper Saddle River, NJ: Pearson Prentice Hall.