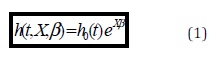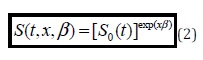Introduction
After the global economy recession of 2008/2009, where many international corporation and financial institutions needed a bail out by government to remain in business, many of the banks operating in Nigeria were found to be distressed. Many of the banks have high ratio of portfolio at risk and are gradually unable to meet payment obligations to both depositors and creditors as they fall due, hence, bank distress was inevitable. Bank distress is not a new phenomenon in Nigeria. The first bank distress was recorded in 1930 when the first indigenous bank, Commercial and Industrial Bank established in 1929 went into liquidation with total deposit liabilities of 23,000 British pound sterling. Bad management, lack of trained manpower, inadequate working capital, poor record keeping and accounting system are among the factors that led to its liquidation. More than Eighty years after, those factors still remain major issues facing the banking industry in Nigeria today. A study carried out by the World bank in 1989 on Nigerian Banks identified poor lending; mismatching of assets and liabilities; weak and ineffective internal control; inadequate policies; lack of standard practices and strategic planning as the major factor responsible for the persistent crises in the Nigeria banking industry (World bank, 1989). After the first banking crisis of 1930, crises have been a regular feature of the Nigeria banking industry. The banking crisis of the 1950s prompted the colonial government to initiate the first banking ordinance of 1952 which took effect in 1954. Since then, so many reforms had taken place in the sector but the crises never stopped.
The 1995 banking crisis is another major turning point in the industry when 57 commercial and merchant banks went into distress within a spate of three months leaving the whole nation in panic. The same trend of the 1990s was about to repeat itself in 2004 when the regulator quickly step in with bank consolidation reforms. In his address on 6th July, 2004, the former Central Bank Governor said “the Nigerian banking system today is fragile and marginal. Our vision is a banking system that is part of the global change, and which is strong, competitive and reliable. It is a banking system which depositors can trust, and investors can rely upon. Evolving such a banking system is a collective responsibility of all agents in the Nigerian economy.” He highlighted factors such as persistent illiquidity, weak corporate governance, poor assets quality, insider abuses, weak capital base, unprofitable operations, and over-dependency on public sector funds, among others, necessitated the 2004 reform (Soludo, 2004). The banks were expected to inject fresh funds where applicable, but most importantly they were encouraged to enter into merger/acquisition arrangements with other relatively smaller banks thus taking the advantage of economies of scale to reduce cost of doing business and enhance competitiveness locally and internationally. This forced the existing 89 banks into voluntary mergers and acquisitions to meet up with the N25 billion minimum capital bases. At the end of the exercise in 2005, 25 banks emerged, but the merger of Stanbic IBTC a year later brings the total number of banks operating in the nation to 24.
Immediately after the 2005 consolidation exercise there are concerns over the state of the industry and the state of readiness of the regulator to meet the challenges of the outcome of the exercise. Bello (2005) commented that the regulatory authority must re-engineer its supervision department and man it with qualified and experienced personnel to carry out this assignment in a professional manner. The automation of the process for the rendition of returns by banks and other financial institutions through the enhanced Financial Analysis Surveillance System (e-FASS) must be driven and implemented with all sense of purpose. The Code of Corporate Governance for Banks in Nigeria post consolidation must be fully implemented to sanitize and reposition the banking industry. – The consolidation exercise was expected to diversified the shareholding structure of the bank, by removing the overwhelming dominance of some pioneer chairman, MD/CEO and instituted a tight code of corporate governance in the industry, with the goal of stemming the tide of banks distress in the country, unfortunately, on August 14th 2010, the current Governor of CBN sacked five managing directors of Nigerian banks, injected N620 billion (approximately $4.1 billion from the CBN, representing 2.5 per cent of Nigeria’s entire 2010 GDP of $167 billion) into the affected banks to prevent systemic failure in the Industry.
According to Sanusi (2010), eight main interdependent factors led to the creation of an extremely fragile financial system that was tipped into crisis by the global financial crisis and recession. These eight 8 factors were; macro-economic instability caused by large and sudden capital inflows, major failures in corporate governance at banks, lack of investor and consumer sophistication, inadequate disclosure and transparency about financial position of Banks, Critical gaps in regulatory framework and regulations, uneven supervision and enforcement, unstructured governance & management processes at the CBN/Weaknesses within the CBN, weaknesses in the business environment. Each of these factors is serious on its own right. Acted together they brought the entire Nigerian financial system to the brink of collapse.
Bank is a financial institution and a financial intermediary that accepts deposits and channels those deposits into lending activities, either directly or through capital markets. A bank holds people’s fund in trust and connects customers that have capital deficits to customers with capital surpluses. Due to their critical status within the financial system and the economy generally, banks are highly regulated. Most banks operate under a system known as fractional reserve banking where they hold only a small reserve of the funds deposited and lend out the rest for profit. They are generally subject to minimum capital requirements which are based on an international set of capital standards, known as the Basel Accords. Since banks are heavily regulated, is there no way to know the state of the banks before they eventually collapse?
Gepp and Kumar (2008) used the survival analysis technique to provide business failure process through the interpretation of the hazard and survival function over time and use the Cox model to interpret and assess the importance of variables that contribute to business failure. Kauffman and Wang (2006) using a multi-method survival analysis to explore the drivers behind Dotcom success and failure, tested for impact of industry, firm and e-commerce specific factors on a DotCom’s sustainable competitive advantage. Steranova and Thomas (2000), shows how using survival analysis tools can help to predict a time till a customer default on their personal loan. Whalen (1991), examined the usefulness of proportional hazard model (PHM) as an early warning tool to bank failure prediction. The results obtained strongly suggest that a PHM with a relatively small number of explanatory variables constructed only from publicly available data could be an effective early warning tool. The overall classification accuracy of the estimated model is high, while both type I and type II error rates are relatively low.
The above analysis shows increase participation in research on business failure prediction particularly using survival analysis technique. Despite increase activities in the sector, trend in research did not provide sufficient justification for the link between business failure prediction and survival analysis techniques in developing countries. Besides, empirical evidence emerging from various studies on business failure prediction models has so far yielded mixed results. Also, none have tested survival analysis technique on bank failure prediction in developing countries that we know of. In a related study, Okezie (2011) examined the relationship between capital ratios and bank distress in Nigeria, and also compare the efficiency of three capital ratios – risk-weighted, leverage and gross revenue ratios, in the prediction of bank distress. Besides this, the research area has not received adequate research attention in Nigeria. The research also shows that most of the studies on business failure prediction that have been reported were carried out in industrialized countries except some few cases in some African countries. This means that there is a major gap in the relevant literature on developing countries, particularly Nigeria.
The collapse and failure of a bank could have devastating consequences to the entire banking system and a widespread repercussion effect on other banks and financial institutions alike. Some of the negative impacts are the massive bail out cost for a failing bank and the negative sentiments and loss of confidence developed by investors and depositors. Very often, bank failures do not occur over night and are usually due to a prolonged period of financial distress. Hence, it is desirable to have an early warning system that identifies potential failing or high-risk banks through financial distress. Various traditional statistical models have been employed to study bank failures. However, these models have not identified the symptoms of financial distress leading to eventual bank failure. This paper attempts to identify the financial distress (the symptoms) that leads to a bank failure using financial covariates derived from publicly available financial statements using Cox proportional hazards model. This is the overall objective of this paper. The specific objectives are to: (i) ascertain the survival time of banks in Nigeria; (ii) ascertain if the survival time differs by specialty (iii) outline the factors that contribute to bank failure in Nigeria; (iv) create the awareness that early warning tools can be used to predict possibility of bank failure even before they occur. In other to achieve the above stated objectives, the following research questions are advanced: (i) what is the survival time of banking business in Nigeria? (ii) Does the survival time differ by area of specialty? (iii) To what extent can early warning tool aid the prediction of bank failure before they occur in Nigeria? (iv) what are the factors that contribute to bank failure in Nigeria? The following null hypotheses are proposed and tested in the course of this study. (i) Banks survival time cannot be predicted in Nigeria. (ii). There is no significant difference between survival time of different specialty of banks in Nigeria. (iii). Factors responsible for bank failure cannot be predicted in Nigeria. The rest of the paper is divided into four sections. In section II, relevant theoretical frame work and literature are reviewed while the methodology of the study is explained in section III. The findings and discussion of result are presented in section IV while section V contains the concluding remarks.
Theoretical Framework and Literature Review
Survival Analysis (SA)
A survival analysis technique is the term applied to a dynamic statistical tool used to analyse the time till a certain event. Thus, the SA approach to Business Failure Prediction (BFP) is fundamentally different from the other approaches mentioned above. While other techniques model BFP as a classification problem, SA models BFP as a timeline, where businesses are represented by lifetime distributions. Lifetime distributions are distributions with a nonnegative random variable that represents the lifetimes of individuals (or businesses) in some population. Lifetime distributions can be characterized by a number of descriptor functions, the most commonly being the survival or hazard function. The survival function S(t) represents the probability that a business will survive past a certain time t, while the hazard function h(t) represents the instantaneous rate of failure at a certain time t. The interpretations of these two functions is very different, but either one can be derived from the other.
There are many different SA techniques available to estimate the survival and hazard descriptor functions. These techniques use past data to calculate the functions at each specific time, but they do not have the ability to make future predictions. Thus, they can be used to analyse past failure to help further the understanding of the failure process. The most popular of these is a non-parametric technique known as the Product-Limit, or Kaplan-Meier, estimator. There is also a less-popular technique called the Nelson-Aalen Additive Estimator. There are also different SA models that define relationships between one of the descriptor functions (usually the survival or hazard function) and the set of explanatory variables. These models can also be used for prediction and are estimated using regression (Kauffman & Wang, 2006).
Review of Survival Analysis in BFP
The pioneering work on SA applied to BFP is by Lane et al. (1986), who used the Cox model to predict bank failure. Lane et al. created their model based on a selection of 334 successful and 130 failed banks from the period 1979 to 1983. The model was then tested on a hold-out sample with one and two year predictions, in which the cut-off value was set at the proportion of failed banks in the sample. The prediction accuracy of the Cox model was found to be comparable with Discriminant Analysis (DA) on the initial and hold-out data, but the Cox model produced lower Type I Errors. In addition, Crapp and Stevenson (1987) applied a Cox model to some Australian credit unions with similar encouraging results.
Laitinen and Luoma (1991) again applied the Cox model to business failure. The significance of this paper is that it was the first to critically present the advantages and disadvantages of using SA to predict business failure. Laitinen and Luoma also empirically compared the classification accuracy of the Cox model with Discriminant Analysis (DA) and Logit Analysis (LA) using 36 failed Finnish limited companies and 36 successful counterparts. Their predictions were made by dividing the businesses into two groups based on their hazard ratios, according to the ratio of failed and successful businesses in the original sample (equal groups in this case). Businesses in the group with the higher and lower hazard ratios were then predicted to fail or succeed respectively. Although the techniques were comparable, DA and LA were found to be slightly superior predictors to the Cox model in this case. Nevertheless, Laitinen and Luoma argued that the SA approach was more natural, appropriate and flexible, and used more information. It was also stated that the empirical underperformance could have been due to the small sample or sample bias inadvertently caused by the authors. Therefore, it was the author’s belief that further research into SA as a BFP tool would result in SA models becoming superior to traditional models. Earlier support was also given by Keasey et al. (1990) and Ogg (1988) who recommended that SA techniques should be used in BFP.
Kauffman and Wang (2001, 2003) used SA techniques to examine the drivers behind the survival of Internet businesses. The data set comprised quarterly data on 100 Internet businesses from the period of 1996 to 2001. Six explanatory variables were used: one industry specific, two businesses specific, two ecommerce specific, and one macroeconomic variable. Two SA techniques were applied to this data: a Kaplan-Meier model was used to perform a descriptive analysis, and the Cox model was used to explore the relative strengths of explanatory variables. Useful conclusions were drawn from both of the SA techniques applied. Although this work did not develop an SA model for predicting business failure, it demonstrated the usefulness of SA techniques for researching the business failure process.
Shumway (2001) applied the first SA model to a data set of significant size. The model was formed using various financial ratios and market-driven variables for over 2000 companies from the NYSE and AMEX over 31 years. This was the pioneering use of a multi-period logit model to estimate the SA model coefficients. This allowed Shumway to estimate an AFT SA model, which had not been previously applied to BFP. Consistent with previous studies, Shumway noted the theoretical superiority of SA techniques over the more popular techniques (DA and LA). In addition, Shumway’s -SA model was shown to empirically outperform both DA and LA in hold-out predictions. However, less than 10% of the businesses in the data set were failed, which is much lower than the percentage in the real world. In addition, Shumway only considered Type I Error.
Laitinen and Kankaanpää (1999) presented a comparative study, in which the Cox model along
with DA, LA, recursive partitioning algorithm (RPA) (a decision tree approach), Artificial Neural Networks (ANN) and Human Information Processing (HIP) were analysed. The six techniques were empirically compared for their 1, 2 and 3 year prediction accuracy using a data set containing three explanatory variables from 76 Finnish companies (with equal number of success and failures). Their analysis showed that SA had superior predictive power for 2 and 3 year predictions. However, they concluded that there were no statistically significant differences in the predictive powers of any of the six models, except for LA being slightly superior to SA for one year predictions.
Overall, there have been few studies on the application of SA to BFP, and most of the previous research has used Cox’s model. Although Lane et al. (1986), Laitinen and Luoma (1991) and many more have indicated that the Cox model was very appropriate for use in BFP, it has not been consistently shown to be superior to traditional techniques. Lane et al. (1986) found the Cox model to slightly empirically outperform DA, but Laitinen and Kankaanpää (1999) found no overall statistical difference between the empirical performance of DA and LA, while Laitinen and Luoma (1991) found both DA and LA empirically superior to SA. Therefore, this study becomes valuable because Nigerian banks data were ran on SA technique to make inference on Nigeria banks’ survival which has never been done before.
Bank Failure Prediction and Survival Analysis Model
Whalen (1991) examined the usefulness of proportional hazard model (PHM) as an early warning tool to bank failure prediction. The results obtained strongly suggest that a PHM with a relatively small number of explanatory variables constructed from publicly available data could be an effective early warning tool. The overall classification accuracy of the estimated model is high, while both type I and type II error rates are relatively low. Furthermore, the model flags a considerable proportion of failures early. As suggested by the author, many further refinements (in variables or in specification, for example) are possible using SA technique. In a similar study, Henebry (1997) uses both cash flow and non-cash flow proportional hazards models to test for stability of the SA models over time. Several different time horizons and start dates were used to test stability over the 1985-1989 time periods. The results indicate that none of the specific formulations were stable across different starting dates nor across different horizons for the same starting date. Forecast models further tested stability and only three variables were found to be consistently useful in predicting bank failure: Primary Capital to Total Assets (PCTA), Nonperforming Loans to Total Loans (NPLTL) and Total Loans to Total Assets (TLTA).
Curry, Elme and Fissel (2004), examined the informational content of market data when these data are incorporated into traditional models that predict bank failures. To assess whether financial markets can provide timely information about firm distress, they first examine the pre-failure behavior of market variables over long periods before failure. The univariate results show distinct patterns of declining prices, negative returns, declining dividends, and rising return volatility several years before failure. Several other market-related measures, however, such as trading volume and share turnover, show no clear trend. They also test for the contribution of market variables in relation to Call Report variables in the prediction of bank failures over the 1989–1995 period. The findings show that selected market variables like equity prices, returns, and volatility of returns add important information to the identification of failed institutions beyond the information contained in quarterly accounting data. They concluded that the in-sample and out-of-sample tests show that the use of market data does improve the sample forecast of bank failure.
King, Nuxoll and Yeager (2005) provide empirical evidence to show that the characteristics of failing banks have changed considerably in the last ten years. They also argue that the time is right for new research employing new empirical techniques. In particular, dynamic models that utilize forward-looking variables and address various types of bank risk individually are promising lines of inquiry. Supervisory agencies should begin to move in these directions, they also describe several examples of this new generation of early-warning models that are not yet widely known among academic banking economists. In response to this, Whalen (2005) develops a Cox proportional hazard model that is designed to predict the probability that a low-risk community bank will be downgraded to high-risk status over an eight-quarter time horizon. The risk dichotomy is made on the basis of CAMELS composite supervisory ratings with a score of 2 separating the low- and high-risk groups. Models are estimated using independent variables measured at year-end 1997, 1998, and 1999 respectively. The out-of-sample forecasting accuracy of the estimated models is examined using data for year-end 2001. In general, the hazard models are found to produce relatively accurate risk classifications out-of-sample. The accuracy of the 1997 specification suggests that these hazard models are relatively stable over time, implying that frequent, costly re-specification is not required. The hazard models are also found to be considerably more accurate than two simpler supervisory screens. Taken together the out-of-sample tests of classification accuracy suggest that this sort of statistical model is a promising, relatively low cost early warning tool.
Hailing and Hayden (2006) in their approach, develop a two-step survival time analysis; a discrete logit model with survival time dummies that allows for time-varying explanatory variables and interval censored data. The empirical analysis reveals that the two step approach outperforms the benchmark logit model with respect to out-of sample prediction accuracy. They found the survival time does not play an important role. The increase in the out-of-sample predictability is mainly driven by the fact that individual predictive models are estimated for at-risk banks. These models partly contain the same variables (capturing credit risk) as the benchmark logit model and partly different variables (e.g. capturing management quality and bank size). The finding supports the argument that in comparison to the entire population of banks, different variables are required to predict failure for banks that face financial problems.
Gomez-Gonzalez and Kiefer (2006), identifies the main bank specific determinants of bank failure during the financial crisis in Colombia using duration analysis. Using partial likelihood estimation, the result shows that the process of failure of financial institutions during that period can be explained by differences in financial health and prudence across institutions. The capitalization ratio is the most significant indicator explaining bank failure. Increases in this ratio lead to a reduction in the hazard rate of failure at any given moment in time. Of special relevance, this ratio exhibits a non-linear component. The results thus provide empirical support for existing regulatory practice. Other important variables explaining bank failure dynamics are bank’s size and profitability.
Halling and Hayden (2007) developed a novel bank failure prediction approach that distinguishes three bank states – operational, at-risk (i.e., vulnerable to default) and financial distress using standard statistical models to predict state transitions. The empirical analysis reveals that this approach significantly outperforms standard two-state hazard rate models with respect to out-of-sample prediction performance. Furthermore, they identify important differences between the subset of at-risk banks and the entire population of banks regarding the set of significant variables to predict default. Management efficiency and size relative to geographically close competitors, for example, are important predictors of financial distress for at-risk banks but not for the entire banking population.
Huang and Friedman (2007) present evidence drawn from historical data, indicating that empirical hazard ratios exhibit pronounced decay over time, contrary to the assumptions of the Cox Proportional Hazard Model do. They provide a possible explanation for this phenomenon, in terms of the evolution, posited by other authors, of the explanatory variables. They propose a hazard rate model with time varying coefficients, which incorporates the decaying hazard ratio property. The model outperforms the standard Cox regression on an out-of-sample/time experiment.
Demyanyk and Hasan (2009) analyzed financial and economic circumstances associated with the U.S. subprime mortgage crisis and the global financial turmoil that has led to severe crises in many countries. They suggested that the level of cross-border holdings of long-term securities between the United States and the rest of the world may indicate a direct link between the turmoil in the securitized market originated in the United States and that in other countries. They also provide a summary of empirical results obtained in several Economics and Operations Research papers that attempt to explain, predict, or suggest remedies for financial crises or banking defaults outlining the methodologies used in each research.
Tung, Quek and Cheng (2009) identify the financial distress (the symptoms) that leads to a bank failure using financial covariates derived from publicly available financial statements using a novel neural fuzzy system named the Generic Self organizing Fuzzy Neural Network (GenSoFNN). Subsequently, the performance of the Cox proportional hazards model is benchmarked against that of the GenSoFNN in predicting bank failures based on a population of 3635 US banks observed over a 21 years period. They found that deterioration of the financial conditions of distressed banks can be observed over time. Thus, the performance of a bank can be tracked and studied from its annual financial statements over a period of time, which essentially is time-series modeling.
Cole and Wu (2009), used a simple dynamic hazard model with time-varying covariates to develop a bank failure early warning model, and then test the out-of-sample forecasting accuracy of this model relative to a simple one-period probit model, such as is used by U.S. banking regulators. By incorporating time-varying covariates, the model enables the utilization of macroeconomic variables, which cannot be incorporated into in a one-period model. They found that the model significantly outperforms the simple probit model with and without the macroeconomic variables. The improvement in accuracy comes both from the time-series bank specific variables and from the time-series macro-economic variables.
Alves, Kalatzis and Maties (2009) analyze private banks survival in Brazil. The banking failure prediction models are able to identify a bank financial condition through the probability of failure. In the research, 66 private Brazilian banks were analyzed, of which 29 are failure banks and 37 are survival banks, between 1994 and 2007. They used the survival analysis technique to find out the main indicators which can explain the private bank failure in Brazil. A Cox proportional hazard model result shows that it was possible to find the main financial ratios to explain the bank failure in Brazil through a construction of a banking failure prediction model.
This study follows that same approach similar to this, thereby filling the literature gap for Sub-Sahara Africa.
Data Collection and Methodology
In this session we discuss data collection and empirical analysis methodologies that was employ in this paper to obtain results and insights on bank failure prediction using survival analysis in Nigeria.
Data Collection
This research is formulated as an empirical design; the data for the bank ratios are collected from the Bank financial statement and the Security and Exchange Commission fact book. In this research, 57 private Nigerian banks were analyzed, of which 39 are failed or acquired banks. Note that the acquisition of the banks is on the premises that they are distress. Eighteen (18) are survival banks. The data are in panel form, covering a period from 2003 – 2011. The dependent variables are in binary form so that we can represent the survival or the failure of a bank in a categorical form, this includes survival, and different degrees of failure, including merger or acquisition by another bank, filling for reorganize, or the total shutdown of a firm. Along with these dependent variables are financial ratios used to predict bank failure process which are described in details below in this section.
Methods for Empirical Analysis
In this paper multiple methods analyses were employed to predict banks survival and failure. First, Kaplan-Meier non-parametric estimator was used to predict survival time of banks, Second, a semi -parametric survival analysis using a proportional hazards model was perform to provide estimate of the impact of financial ratios variable used on survival rate of banks in Nigeria. The non-parametric techniques were also used to estimate the survival functions for specialty of banks.
Semi parametric Analysis
The Cox (1972, 1975) proportional hazards model was used to analyze the bank survival data obtained for the study. Similar to Alves, Kalatzis and Maties (2009), we estimated the hazard model based on predetermined financial ratios. The survival time being estimated as the calendar time for the banks selected for the study, the selection of banks in this study is based on availability of publicly available data. The primary aspects that calendar time survival analysis can shed light on the general economic backdrop to bank performance. The bank financial ratio will be more revealing of firm-level issues that are either amplified or suppressed by banks in time of operation.
In the analysis of firm survival, we can observe the failure time of a firm, or its continued operation. Since we can only observe what is happening with the banks up to the present, and some will continue to operate, our data set was right-censored. Thus, a firm in our sample will still be at risk at time t if its survival time or the censored time is greater than or equal to t. The Cox model assumes the following functional form for the hazard function:
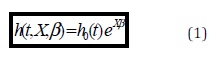
In Equation 1, h0 (t) is the unknown baseline hazard function and β is a vector of parameters to be estimated. This expression enables us to capture the baseline hazard rate as a result of the age of the firm via h0 (t), and the impact of other factors that vary across banks through their vector of time-varying covariates, X, (which are the financial ratios) via the estimated parameters, β.
Based on this hazard function, the corresponding survival function is given by: 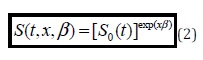
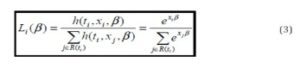
In Equation 2, S0 (t)ε {0,1} is the baseline survival function. This expression represents the likelihood that a bank will continue to be in existence at time t, in view of the baseline rate of survival among observed banks in the Nigerian economy, banks financial ratio related to bank survival were employed as the covariates given the scope of the paper from 2003 to 2011 and given that it has been in operation continuously in prior periods. For a bank i that is still at risk at time ti, its likelihood of failure at time ti compared to other banks that are at risk at time tiis given by
In Equation 3, R (ti) is the set of all firms that are still at risk at time ti. For a data set that contain n banks, the partial likelihood is given by:

In Equation 4, ci is 1 if the observation is not censored and 0 if the observation is censored. Using this partial likelihood function, the parameters can be estimated without specifying the baseline hazard function.
Following Honjo (2000), we further develop a multiplicative hazards model based on calendar time. Instead of comparing firms at the same age, we now compare them at the same calendar time. The function, , now denotes the baseline hazard function based on calendar time. It allows us to incorporate the impact of the macroeconomic variable into the baseline hazard function.
Nonparametric Analysis: As an alternative method, we will report on the results of a nonparametric analysis, for which we will use the Kaplan-Meier estimator to estimate the survival function (Hosmer and Lemeshow, 1999). The Kaplan-Meier estimator is defined as:

Where ni is the number of firms that are still at risk at time ti and di is the number of firms that actually failed at time ti. The Kaplan-Meier estimator provides a reading on the likelihood of survival at time t based on the survival history of all firms. Using results from the semi parametric analysis, we stratify the data set into different subgroups (Commercial & Merchant banks) and calculate the Kaplan-Meier estimator for each group to know the survival time for each group. We then use standard statistical tests to compare the differences among the groups and compare the results with our regression results from the proportional hazards models.
Cox Regression Model Specification
As discussed earlier, Cox regression model is a common technique used for comparing the survival time among treatment levels and taking into account the covariate effects with the presence of censored cases. This is also known as a proportional hazard model. Proportional hazard model assumes that the covariate effect on a hazard function is the same for different factor levels for all time points. That is, the ratio of the hazard functions for two individuals with values of covariate vectors x1 and x2 does not vary with time t. This implies that the hazard function of t given covariates x can be written as h(t|x) = h0(t)g(x). h0(t) is the baseline hazard function where g(x) = 1.
Therefore
Log h0(t) = α+β1xi1(t)+β2xi2 (t) +…+βKxik ……………………………………….. (6)
Where
X takes the form of X1….X12. This model was adopted in this study using financial ratios as the covariate. Hence it was specified as follows:
Log h0(t) = α(t)+β1Xi1+β2Xi2 + β3Xi3 +β4Xi4+β5Xi5+β6Xi6+β7Xi7+…..β10Xi10+u1 ………… (7)
Where
i is a subscript for observation
Xs’ are the covariates
α is a constant that represents the log baseline and
Log h0(t) takes a binary form, 1 if death occurs and 0 if death does not occur
β = is the vector of parameters to be estimated.
The predictor variables are given as X1, X2, X3, X4, X5, X6, X7 ……………………and X10;
Where X1 is a categorical variable used as treatment levels,
X1, = Reform (1) Period before 2004 bank consolidation reform, Reform (2) 2004 bank consolidation reform, Reform (3) 2009 financial crisis reform, these three variables
X2, = (TLTA) – Total loan and advances to total asset of the banks
X3, = (LTLTA) – Long term liability to total asset of the banks
X4, = (TBDTA) – Total bank deposit to total asset
X5, = (ROA) – Consolidated net income to average total asset
X6, = (OEATA) – operating expenses to average total asset
X7, = (SFATA) – Shareholders funds to average total asset
X8, = (NPLTA) – Non performing loan to average total asset
X9, = (NPLTLL) – Non performing loan to total loan and lease
X10, = (TLATD) – Total loan and advances to total deposit
and U1 = Error term
A priori, β1 > 0; β2 > 0; β3 > 0; β4 > 0; β5 > 0; β6> 0; β7 > 0, β8; β9; β10 < 0
Variable Definitions/Measurement
Dependent variable
Firm survival S0(t) – Hazard ratio h0(t) takes a binary form 1 is assigned if the firm is in-active during the course of the study and 0 is assigned if the firm is active and performing.
Independent variables
TLTA – Total loan and advances to total asset of the banks
LTLTA – Long term liability to total asset of the banks
TBDTA – Total bank deposit to total asset
ROA – Consolidated net income to average total asset
OEATA – operating expenses to average total asset
SFATA – Shareholders funds to average total asset
NPLTA – Non performing loan to average total asset
NPLTLL – Non performing loan to total loan and lease
TLATD – Total loan and advances to total deposit
Result and Discussion
Kaplan –Meier Survival Analysis Estimate
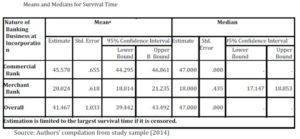
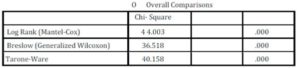
Kaplan-Meier survival probability estimates and plots were used to compare the survival time of different specialty of banks with regards to the banking sector reforms for a period of 2003 to 2011. Table 1 show that commercial banks have higher survival time of 45.57 years while merchant banks have survival time of 20.04 years. By 2007 all the banks in Nigeria have adopted the Universal banking business nature; this was taken into consideration in the study. The result obtained shows the average survival time up to 2007. Survival time for the total sample is 41.67 years with strong association with the wave of reform that was introduce in 2004 but took effect in 2005 reporting year. This simply implies that average survival time for banks in Nigeria is 41years particularly with regards to when the banks seize to exist as specialty bank. The significance of the estimate was tested using three diagnostic tests. Table 2 shows the result of the three tests, Log rank, Breslow (generalized wilcoxon) and Terone Ware were all significant at 1%. The result implies that there is a statistical evidence to show that the survival time for specialty of banks (commercial and merchant) banks differs significantly in Nigeria.
Table 1: Kaplan Meier Survival Estimate by Specialty
Table 2: Diagnostic Test Kaplan Meier Estimate
Test of equality of survival distributions for the different levels of Nature of Banking at Incorporation
Authors’ compilation from study sample (2014)
Table 3: Adjusted Hazard Ratios from Cox Proportional Hazard Model
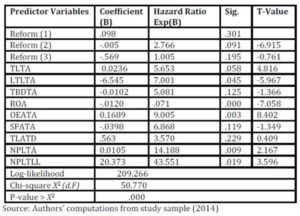
Table 3 shows hazard ratios estimated from Cox regression. The Table shows that the survival of banks in Nigeria is most strongly influenced by 10 predictor variables (one reform levels which is used as treatment for the survival of banks in the equation and nine financial ratios) used for the survival analysis. The reform variable is categorize into three periods, the period before the 2004 reform, the 2004 bank consolidation reform and the 2009 financial reform respectively. The Nine (9) influential financial ratio variables are total loan to total asset of the banks (TLTA), long term liability to total bank asset (LTLTA), total bank deposit to total asset(TBDTA), net income to average total asset (ROA), operating expenses to average total asset (OEATA), shareholders funds to average total asset (SFATA), non-performing loan to average total asset (NPLATA), non-performing loan to total loan and advance plus lease (NPLATLL), total loan and advance to total deposit (TLATD). All the estimated coefficients exhibit the correct sign and are highly significant except for two reform variables 1 and 3 and three financial ratio variables. However it should be noted that, just as in multiple regression analysis, collinearity among explanatory variable can be a problem, therefore this specification is parsimonious. Many ratios have been considered to arrive at this level (see appendix). This study derive the survival function from the underlying hazard function as stated in the model specification, it should be noted that the coefficient from the hazard function appear in the survival function changed. As a result, in a survivor function coefficients can be expected to exhibit counterintuitive signs. Coefficients that are expected to be positively associated with the probability of survival will show as negative and vice versa. For instance return on asset will exhibit negative sign. Similarly, variables that are expected to be negatively associated with the probability of survival, such as the operating expenses ratio or the non-performing ratio will have positive coefficient.
Table 3 above show that the variables that exhibited the strongest statistical relationship to the probability of bank survival is operating expenses to total average asset ratio. The ratio shows the percentage of bank asset being use for operating expense. The ratios show a t-value of 8.4 and a hazard ratio of 9.0.This simply implies that banks with high operating expense ratio is 9 times more likely to fail than banks that are low on operating expenses, this result is also similar to the result obtained in Whalen 1991. That was not the ratio with the highest hazard ratio, non-performing loan to total loan plus lease has the highest hazard ratio of 43.5 which implies that banks that have a high measure of its total loan plus lease as non-performing is 43.5 times more likely to fail than banks that do not. Both ratios are significant at 1% respectively.
The study shows return on asset to have a t-value of 7.0. Return on asset ratio shows the extent the banks are able to use their asset to generate income. The result of the ratio to survival probability show that banks that are able to generate high return on their asset are .17 times more likely to fail than banks that do not. With a result of .17 such banks are more or less not likely to fail. The result is also significant at 1% statistical level. The hazard ratio of the variable total loan to total asset is 5.6. This shows that banks that are high on total loan to total asset are 5.6 times more likely to fail in comparison with banks that are low on total loan to total asset. The variable has a t-value of 4.8 and it is also statistically significant at 5%. The hazard ratio of the variable long term liability to total asset is 7.0. This shows that bank that are high on long term liability than their total asset can accommodate are 7 times more likely to fail in comparison with banks that are moderate on their long term liability. The long term liability ratio show the extent the bank commits their asset to long term obligations. The ratio has to be favourable to impact positively on the survival of the bank. The result is significant at 5%.
The hazard ratio of the variable total bank deposit to total asset (TBDTA) is 5.0. The ratio shows the extent of liability of the bank to his customers. The result shows that banks that are high on total deposit to total asset are 5 times likely to fail to banks that are not. The result is not correctly sign and also not significant hence it cannot be use to make inferences. The hazard ratio of shareholders fund to total asset is 6.86. This shows that banks that that are low on their shareholders fund to total asset are 6.8 times likely to fail than banks that are high on their shareholders fund. The ratio of shareholder’s fund shows the extent of the shareholders commitment to the business. The result obtained though correctly sign but not significant to make inferences. This could imply that the capital base of most Nigerian bank is still not adequate to their survival probability. The hazard ratio of total loan and advance to total deposit shows a ratio of 3.5. The ratio total loan to total deposit show the measure of the banks’ total loan to their deposit liability and the extent the banks is using their deposit to generate loan income. The result obtained implies that banks that are high on total loan to their total deposit are 3.5 times likely to fail than banks that are not. The result obtain is not statistically significant hence, it cannot be use for inferences. The hazard ratio of the variable, non-performing loan to average total asset show a ratio of 14.18. This ratio show the extent the total asset of the bank can accommodate it non performing loan. The 14.18 hazard ratio shows that banks that are high on their non-performing loan to total assets are 14 times more likely to fail than banks that are not. The result obtain is significant at 10%. The result implies that 1% decrease in the ratio will improve the bank chances of survival by 14%. Finally, as mentioned earlier the reform variable was used as treatment level and the result show that treatment level 2 is significant, the reform level 2 is a proxy for 2004 bank consolidation reform. The result show a hazard ratio of 2.76, which implies that the reform activities of 2004 enhance bank survival two times as much as it would have otherwise be. This implies that 1% increase of such reform activities will improve bank survival time at least twice. Recall that the major focus of the 2004 bank consolidation reform is the increase of the bank capital from N2billion to N25 billion naira (approximately $173 million), this action has help to ensure bank survival at least 2 times better. Also the 2009/2010 financial crisis reform also show positive influence on survival but the result is not significant like the 2004 reform which is significant at 1% and a statistical relationship of 6.9.
The adequacy of the fitted Cox model was assessed using log-minus-log plots, the likelihood ratio test and the AIC (Akaike’s Information Criterion) as diagnostic procedures. All log-minus-log plots were parallel, showing that the assumption of proportional hazards was satisfied. The p-value from the likelihood ratio test was small (0.0001 < 0.05), thereby showing that the 10 variables constituting the fitted Cox model were jointly efficient in explaining the long-term survival of banks in Nigeria at the 5% level of significance.
The key objective of this aspect of the study is to test the ability of the financial ratios to predict banks survival and to identify influential variables that affect the survival of banks in Nigeria, particularly in assessing the degree of importance of financial ratios in predicting long-term survival of banks in Nigeria. Six (6) of the 9 financial ratio predictor variables in Table 3 is highly significant to measure the survival of banks in Nigeria.
The overall statistics show the log likelihood of 209.266 which is high and significant at 1% when compared with the critical Chi square at 5% = 31.4, therefore, the final decision is to reject the null hypothesis and accept the alternative hypothesis. This implies that factors responsible for bank failure can be predicted in Nigeria.
Summary Conclusion and Recommendations
In this paper we propose and empirically evaluate survival time models to predict bank failure using financial ratios as predictor variables in Nigeria. The research question has been addressed before by several papers (see Lane et al. (1986), Whalen (1991), Henebry (1997)). We extend this literature in several ways. First, the banking sector reforms were introduced as the treatment variable thereby showing the effect of banking reform on survival time of the banks in Nigeria. Secondly, we took the analysis further by showing the survival time for each specialty of banking business that has been in operation in the country up till 2007 when the banking business nomenclature changes in Nigeria and all the banks adopted universal banking business. The analyses in this study also show the effect of estimated financial ratios on survival probability of banks in Nigeria. The data for the study was sourced from the banks financial statement and the Nigeria security market fact book. The result from this study reveals that we can predict factors at the firm level that contributes to bank failure.
The number of variables used for the study was reduced to 10 using the stepwise backward elimination procedure. The stepwise backward elimination procedure was applied with a probability cut-off point of 0.20. At each stage of elimination, variables that could not meet the minimum criteria for staying in the model or “useless variables” were discarded. The procedure of discarding “useless variables” was continued until no more “useless variables” could be removed from the model. The final model consisted of 10 highly influential predictors of bank survival. The P-values were fixed at the 5% level of Significance. P-value smaller than 0.05 indicates the significance of variables while p-value greater than or equal to 0.05 indicates insignificance. The aim of the study was to identify factors that significantly affect the long-term survival bank. Analysis was done using the Cox proportional hazards model, in view of the fact that some of the 57 banks in the study were right censored. Hazard ratios were obtained for key influential predictors of survival. Kaplan-Meier survival probability curves were used for determining average survival time of specialty of banks. Descriptive and summary statistics were also obtained. The adequacy of the fitted Cox regression model was assessed using the likelihood ratio test and Akaike’s information criterion (AIC) statistic. The fulfillment of the proportional hazards assumption was tested by use of log-minus-log plots.
The highlight of the result shows that banks that are high on non-performing loan to total loan and advances plus lease are 43 times more likely to fail than banks that are not. The result also shows that banks that are high on non-performing loan to total asset are 14 times more likely to fail than banks that are not. This result is consistent to the result obtained by Henbry, 1997. This makes the issue of non-performing loan to be very important to the banks as well as to the bank regulator. The result of the findings tells regulators the ratios to watch for to ensure that the health of the banks is not jeopardize. Other ratios of importance in this analysis are the result obtained on operating expenses to average total asset ratio. The ratio shows that banks that are high on operating expense are 9 times more likely to fail than banks that are not. The findings of this study coincide with other study of this nature and this is an innovation in usage of Nigeria data.
Although the result from this study show the use of financial ratios in predicting long term bank survival is a good development in the Nigerian research circle, but far beyond financial ratios there are other more important variables that contributes to bank failure at the firm level such as management quality, corporate governance practice, and internal efficiency rating that are not eventually captured in this study even though they are considered initially. A good, efficient and innovative management is especially important in situations of financial crisis and in a developing economy like Nigeria. Other macroeconomic variables such as rate of employment, exchange rate and level of inflation in the economy are other important variables in predicting bank failure. The macroeconomic environment determines the business environment the banks operate in and this affects the survival of the bank. Despite the limitations, this paper provides a good starting point in predicting bank failure in Nigeria. The fact that the result from this study shows clearly the predictor variables that affects bank long term survival in Nigeria implies that this paper can be improved upon to capture other variables of interest in subsequent studies.
The study therefore recommend that the reform activities of the government should be well thought out and strategies for implementation should be put in place like we have in the 2004 reforms to enable it have effective positive impact on the banking sector in Nigeria.
The banks should be mindful of the non-performing loan and operational expenses and ensure it is well manage and not in excess of their average total asset. The regulator needs to build capacity and ensure that the banks return are well analyse as they are sent to them to detect signs of distress early before the banks went down.
(adsbygoogle = window.adsbygoogle || []).push({});
References
1. Alves, K. L., Kalatzis, A. E. and Matias, A. B. (2009). Survival Analysis of Private Banks in Brazil available online at http://ecomod.net/sites/default/files/documentconference/ecomod2009/1058.pdf
2. Bello (2005). Banks Consolidation and N25bn Recapitalization -Another Perspective, [Online], [Retrieved on June 18, 2012], http://www.gamji.com/article6000/NEWS6057.htm
3. Bekele, E and W. Zeleke, (2008). ‘Factors that Affect the Long-term Survival of Micro, Small and Medium Enterprises in Ethiopia,’ South African Journal of Economics, 76 (3), 1-33.
Publisher – Google Scholar
4. Cole R. A. and Wu Q. L (2009). Predicting bank failures using a simple dynamic hazard model retrieve [Online], [Retrieved December 3, 2010], http://www.fdic.gov/bank/analytical/cfr/2009/may/CFR_Cole_Wu_EWS_Draft_05_19_09.pdf
5. Crapp, H. R. and Stevenson, M. (1987). Development of a Method to Assess the Relevant Variables and the Probability of Financial Distress, Australian Journal of Management, 12(2), 221-236.
Publisher – Google Scholar
6. Curry, T.J., Peter J.E and Gary S. F (2004) Can the Equity Markets Help Predict Bank Failures? Working Paper 2004-03, [Online], [Retrieved May 10, 2012] http://www.fdic.gov/bank/analytical/working/wp2004_03/wp2004_03.pdf
7. Demyanyk, Y. and Hasan, I. (2009).Financial Crises and Bank Failures: A Review of Prediction Methods, working paper 09-04, Federal Reserve Bank of Cleveland, [Online], [Retrieved July 13, 2012] http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1422708
8. Gepp A. and Kumar, K. (2008), ‘The Role of Survival Analysis in Financial Distress Prediction’, International Research Journal of Finance and Economics, 16, pp 13 – 34.
Google Scholar
9. Gomez-Gonzalez, J.E. (2006), Explaining Time to Bank Failure in Colombia during the Financial Crisis of the Late 1990s, Cornell University and Banco de la República, Nicholas M. Kiefer Cornell University, [Online], [Retrieved June 13, 2011], http:/banrep.gov.co/docum/ftp/borra400.pdf
Google Scholar
10. Gomez-Gonzalez, J.E. and Keifer N.M (2006), Bank Failure: Evidence from Colombia Banking Crisis, CAE working paper N06 – 12,[Online], [Retrieved June 28, 2012] http//.economics.cornell.edu/cae/06-12.pdf
11. Halling, M. and Hayden, E. (2006). Bank Failure Prediction: A Two-Step Survival Time Approach, [Online], [Retrieved June 18th 2010], http://homepage.univie.ac.at/evelyn.hayden/
Google Scholar
12. Halling, M. and Hayden,E. (2007), Bank Failure Prediction: A Three-State Approach, Working Paper, Oesterreichische National bank and University of Utah, [Online], [Retrieved June 18th 2010], http://homepage.univie.ac.at/evelyn.hayden/
Google Scholar
13. Huang, J. and Friedman, C. (2007), Modeling Multi-Period Corporate Default Probability when Hazard Ratios Decay, [Online], [Retrieved April 12, 2010] http://www.bis.org/ifc/publ/ifcb28h.pdf
Google Scholar
14. Henebry, K. L. (1997). ‘A Test of the Temporal Stability of Proportional Hazards Models for Predicting Bank Failure’, Journal Of Financial And Strategic Decisions, Vol. 10(3), pp 1- 11
Google Scholar
15. Kauffman, R.J., and Wang, B. (2001), ‘New Buyers’ Arrival Under Dynamic Pricing Market Microstructure: The Case of Group-Buying Discounts of the Internet’, Journal of Management Information Systems, 18, 2 (Fall 2001).
Google Scholar
16. Keasey, K., McGuinness, P. and Short, H. (1990). ‘Multilogit Approach to Predicting Corporate Failure: Further Analysis and the Issue of Signal Consistency,’ Omega, 18(1), 85-94.
Publisher – Google Scholar
17. Laitinen, E. K. and Luoma, M. (1991). ‘Survival Analysis as a Tool for Company Failure Prediction,’ Omega, 19(6). 673-678.
Publisher – Google Scholar
18. Laitinen, T. and Kankaanpää, M. (1999).’Comparative analysis of failure prediction methods: the Finnish Case’, The European Accounting Review, 8(1), 67-92.
Publisher – Google Scholar
19. Lane, W. R., Looney, S. W., and Wansley, J.W. (1986). ‘An Application of the Cox Proportional Hazards Model to Bank Failure’, Journal of Banking and Finance, 10(4), 511-531.
Publisher
20. Okozie A. C., (2011). ‘Capital Ratios as Predictors of Distress: A Case Study of the Nigerian Banking System’, Global Journal of Human Social Science, Vol. 11( 3), pp 46 – 55.
Google Scholar
21. Ogg, P. J. (1988). ‘Quantitative Aspects of Modelling Financial Distress’. Working Paper. Submitted to The Inaugural Australasian Finance and Banking Conference without acceptance.
22. Thomas B. King, T.B., Nuxoll, D. A., and Yeager, T.J. (2005). Are the Causes of Bank Distress Changing? Can Researchers Keep Up? Federal Reserve Bank of St. Louis Publication. [Online], [Retrieved June 18th] http://research.stlouisfed.org/publications/review/06/01/KingNuxollYeager.pdf
Google Scholar
23. Tung, W.L., C. Quek and P. Y.K., Cheng (Undated), Bank Failure Prediction and Financial Data Reconstruction using Novel Soft-Computing Approaches, [Online], [Retrieved July 10, 2011] http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.19.6509
Google Scholar
24. Whalen, G. (1991). ‘A Proportional Hazards Model of Bank Failure: An Examination of its Usefulness as an Early Warning Tool, Federal Reserve Bank of Cleveland’, unpublished manuscript, [Online], [Retrieved May 8 2012] http://www.clevelandfed.org/research/review/1991/91-q1-whalen.pdf
Google Scholar
25. Whalen, G., (2005), A Hazard Model of Camels Downgrades of Low-risk Community Banks, Economics Working Paper 2005-1, [Online], [Retrieved May 8, 2010] http://www.occ.gov/publications/publications-by-type/economics-working-papers/2008-2000/wp2005-1.pdf
Google Scholar
26. Sanusi, S.L. (2010). ‘The Nigerian Banking Industry: What Went Wrong and the Way Forward’, Convocation Lecture, delivered at Bayero University, Kano, Central bank of Nigeria. [Online], [Retrieved September 2, 2011] http://www.cenbank.org/OUT/SPEECHES/2010
Google Scholar
27. Shumway, T. (2001). ‘Forecasting Bankruptcy More Accurately: A Simple Hazard Model’. The Journal of Business, 74(1), 101-124.
Publisher – Google Scholar
28. Soludo, C.C (2004). ‘Consolidating the Nigerian Banking Industry to Meet the Development Challenges of the 21st Century’, An Address delivered to the Special Meeting of the Bankers’ Committee, July 6, at the CBN Headquarter, Abuja. Central bank of Nigeria. [Online], [Retrieved September 2, 2010] http://www.cenbank.org/OUT/SPEECHES/2010
Google Scholar
29. Stapanova, M. and Thomas, L., (2000). Survival Analysis Methods for Personal Loan Data, [Online], [Retrieved September 20, 2012], http://teaching.ust.hk/~ismt253w/cox.pdf on 7/5