Introduction
Gasification is a thermo-chemical process aimed at converting a solid fuel into a combustible synthesis gas. Gasification was well known and widely used in the past century: many large and small scale reactors were installed, above all for coal gasification. Nowadays, due to the environmental issues strictly connected to greenhouse effect, the scientific community has turned its interest to biomass fuels, characterized by a closed CO2 loop. In fact, being the carbon dioxide produced by combustion equal to that absorbed by plants during their life cycle, the CO2 amount in the atmosphere is not increased when exploiting biomass for energy production.
Biomass and coal present several differences, both from a physical and from a chemical point of view:
- Volatile matter: coals present a lower average percentage of volatiles compared to biomasses; biomass shows values in the range 30-70%, coal values range from 5% (Anthracite) to 40% (bituminous coals);
- Sulfur content: coals are characterized by a higher sulfur percentage (about 1%) compared to biomass fuels, which in most cases do not exceed 0.1%;
- Ash content: biomass fuels often show a lower ash percentage compared to coals, the latter being in the range 6-12% or more for low grade coals;
- Oxygen content: in terms of ultimate analysis, biomasses present oxygen contents higher than 40%, whereas coals do not exceed 10%;
- Lower heating value: coals values are around 30 MJ/kg; biomasses keep around 18-22 MJ/kg.
The many dissimilarities between these two fuel types largely influence the composition and temperature of the products yielded by the conversion process, determining significant variations of the gasification efficiency.
It is worth to remark that a first principle analysis (based on an energy balance) performed on a gasification system would lead to global efficiency values very close to one, being energy losses limited to thermal dispersion phenomena or gas leakages; instead, an exergetic balance-based analysis will emphasize the losses connected to aspects that go beyond first principle effects. A study on exergetic efficiency for a gasification process using pure oxygen and steam as oxidizers was published in 2007 by Prins et al. ( “From Coal to Biomass Gasification: Comparison of Thermodynamic Efficiency”), providing interesting results about the suitability of the different fuel types in the gasification process.
The present paper studies the air gasification process second principle efficiency for different biomass and fossil fuels, through tests carried out by an equilibrium model. In Section 4, a comparison with the results obtained by Prins et al. in 2007 is effected; in order to underline the differences between oxygen-steam and air processes. Prins’ study is taken as reference paper for the oxygen gasification.
The results presented demonstrate that air gasification may be considered as a suitable conversion process for biomass fuels under well defined reaction temperature limits.
In Section 5 is presented the application to biomass fuels of an equilibrium model modified on the ground of experimental data to account for the main non-equilibrium effects of gasification. The modified model is employed to evaluate the exergetic efficiencies under real gasification conditions.
Method of Analysis
In the present work, several simulations are carried out through an equilibrium biomass gasification model published in 2009 and 2010 by Damiani and Trucco. Despite its simplicity and low precision in predicting the actual gas composition, the equilibrium model is a useful tool for the exergetic analysis of different fuels gasification, since it simulates the ideal reaction, cleaned of all the effects connected to the reactor (leakages, heat losses, mixing …) and to the chemical kinetics of the process; it is thus able to express the maximum conversion potential for a certain fuel. The assumption of conversion process ideality is made also when studying the effect of a fuel on the performance of an internal combustion engine: in the mathematical model is implemented the engine “limit cycle”, in order to compare the different fuels tested on a common basis. The same observations were made by Prins et al. in their studies of 2003, 2005 and 2007 concerning gasification efficiency; in fact the results presented in the reference paper [1] “From Coal to Biomass Gasification: Comparison of Thermodynamic Efficiency” were obtained through equilibrium modeling.
Exergy Calculations for Gasification Reactions
As known, exergy is the maximum work obtainable by a reversible transformation that leads a system to be in equilibrium with an “environment” in a reference state; the system exchanges heat only with the aforementioned environment.
It is assumed that the environment is of large size, thus keeps constant its intensive variables, whereas its extensive variables (enthalpy, entropy, volume…) can change during the transformation; temperature, pressure and chemical composition are known. Once the system is in equilibrium with the environment, the possibility of generating work by the interaction between system and environment is exhausted and the system has reached its “dead state”.
The exergy associated to a solid, a liquid or a gas depends on chemical composition (chemical exergy) and on pressure and temperature (physical exergy).
According to the books of Bejan et al. (1996) and of Wark (1995), chemical exergy for a substance can be:
- “Non reacting” chemical exergy: it is related to the substances present in the reference environment, which —as said — has known composition. “Non reacting” chemical exergy can be calculated as the reversible work obtained by diluting the substance in exam down to the reference concentration value assumed for the environment.
- “Reacting” chemical exergy: it is related to the substances not present in the reference environment composition. For a fuel, “reacting” chemical exergy can be calculated as the reversible work obtained by a complete combustion transforming the fuel into reaction products present in the environment, plus the work developed by the dilution of these products down to the reference environment concentration.
For fuels combustion and gasification, the reference environment is at p0 = 101 325 Pa and T0 = 298.15 K, and presents the chemical composition of standard atmospheric air with 70% relative humidity, as advised by Szargut’s paper of 1989.
The total exergy associated to the ith substance is expressed in Equation (1):
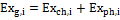 (1)
(1)
Where the subscript g stands for global, and the subscripts ch and ph for respectively chemical and physical. The expressions utilized to quantify the exergy content for the substances considered in a gasification process are introduced in the following.
1) Exergy of the syngas. The expression of exergy content for a gas mixture was utilized. The latter appeared in the book by Sato (2004):

As can be observed, in Equation (2) four terms provide their contribution to the gas mixture exergy content.
- Chemical exergy of gas mixture components; the chemical exergy of each gas species (Ex0i) is indicated in Table 1; the values are derived from the publications of Ptasinski et al. (2007) and of Bejan et al. (2006).

2) Exergy of the charcoal. For a substance in the solid state, the expression to be utilized to calculate physical exergy content is indicated in Equation (3):
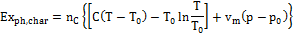 (3)
(3)
Being C the solid thermal capacity and vm the molar volume calculated at temperature T0. Charcoal chemical exergy content, is indicated in Table 1.
3) Exergy of the fuel. To calculate the exergy associated to the moisture – free fuel entering the reactor, the Szargut and Styrylska correlation (1964) was used, according to which fuel exergy is proportional to its lower heating value. Considering 1 kmol of fuel:
 (4)
(4)
In Equation (4), the value of the proportionality constant β, depends on the biomass O/C and H/C ratios. β was calculated through proper expressions published in Baher’s book of 1968. Fuel physical exergy can be neglected, since it is possible to assume fuel thermal equilibrium with the reference environment.
4) Exergy of the oxidizer stream. Air entering the reaction volume is considered dry, composed of 21% O2 and 79% N2 in volume. Air chemical exergy can be neglected, being reference environment composition very close to that of the air model utilized. Also air physical exergy was neglected, since the gasification was carried out with air at ambient conditions.
Exergetic Efficiency for Gasification
The main parameter to be considered when evaluating the performance of a process is its “efficiency”, defined, in general terms, as the ratio between the “useful effect obtained by the process” and the “expense encountered to obtain it”. Efficiency may be evaluated on an energetic or on an exergetic basis.
The definition of the terms “expense” and “useful effect” is not unique: the study by Baher and others (1968), so that the study of Grassman (1950) concludes that, for a system composed by K entering and N exiting streams of matter, the number of possible efficiency definitions is given by the product N·K.
For a gasification process, two entering streams (biomass and oxidizer) and two exiting streams (charcoal and biogas) are present, thus four different definitions of the exergetic efficiency are possible; in the following, just two definitions will be employed to calculate the global exergetic efficiency:
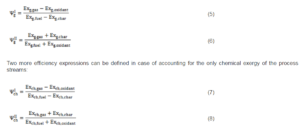
Observing Equations (5), (6), (7) and (8) it is possible to remark that:
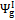 and
and 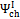 are the ratios between exergy increase of gaseous stream and exergy decrease of solid stream;
are the ratios between exergy increase of gaseous stream and exergy decrease of solid stream;
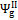 and
and 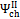 indicate the process inlet-to-outlet efficiency, since they put in relation the exergy of exiting stream (gas and charcoal) with that of the entering stream (biomass and oxidizer);
indicate the process inlet-to-outlet efficiency, since they put in relation the exergy of exiting stream (gas and charcoal) with that of the entering stream (biomass and oxidizer);
An additional consideration should be pointed out: in most cases, the hot producer gas thermal content is not used to generate work; thus, a variable accounting for the thermal exergy lost with the hot gas stream is proposed in Equation (9):
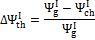 (9)
(9)
This variable indicates the fraction of the global exergetic efficiency that is lost due to physical exergy content of the products leaving the reactor at a significant temperature.
The Biomass Gasification Model
As previously mentioned, the calculations of gas composition and temperature were carried out by an equilibrium model; the latter was integrated with the implementation of the expressions indicated in Equations 1 to 4, in order to compute the exergy of all the streams involved in the process; to calculate the gasification exergetic efficiency values, also Equations (5) to (9) were included in the model.
According to the 2003 study conducted by Prins et al., two different methodologies exist to deal with the construction of an equilibrium model, substantially equivalent in the results: a “stoichiometric approach”, based on the calculation of equilibrium constants for the reactions involved in the process, and a “non stoichiometric approach”, based on the minimization of Gibbs free energy. The first approach is more strictly connected to the physics of the phenomena, since it imposes the equilibrium of well defined reactions occurring in the system; the second approach solves the problem by minimizing the Gibbs free energy function, with the imposition of non-negativity and mass-closure constraints, not considering particular chemical reactions and species involved. The model presented in this paper is of the “stoichiometric” type.
The model operates under the assumptions of steady state, design-point biomass feeding rate (in order to avoid considering the influence of reactor load on gasification performance), perfect gas behavior for all of the gaseous compounds, complete Tar conversion, reactor solid output composed of pure carbon, equilibrium conditions both for solid and for gaseous reactor output.
In the papers by Damiani and Trucco a thorough description of the biomass gasification model is provided, so as the complete set of equations implemented. The model employed for tests was tuned over the experimental facility described in the paper by Chern, Walawender and Fan (1991). Such facility is an air blown atmospheric downdraft unit, with a diameter of 0.6 m and a feed-rate in the range 23-127 kg/h.
The Fuels Investigated
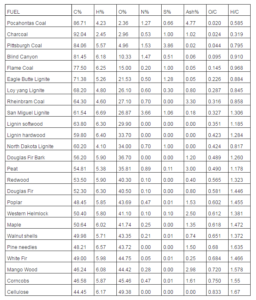
Table 2 lists the fuels considered in the present paper (biomasses and coals) and provides their ultimate analysis, indicating the mass percentages of carbon, hydrogen, oxygen, nitrogen, sulfur and ash, together with the O/C and H/C ratios (respectively, oxygen to carbon and hydrogen to carbon molar ratios). The data were taken from websites dealing with biomass processes (www.woodgas.com), energy (http://www.anl.gov) and chemical engineering (www.et.byu.edu).
Figure 1 shows the van Krevelen diagram for the fuels listed in Table 2. In the diagram, some typical fuels as Average Wood Lignin and Cellulose are indicated with different symbols. It has to be remarked that the heating value of the fuels positioned on the van Krevelen diagram increases with O/C ratio decreasing.
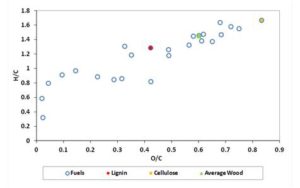
Figure 1: Van Krevelen Diagram for the Solid Fuels Tested
Table 2: Solid Fuels Considered in the Present Study. The Composition Values are Expressed in Mass Percentages
Comparison between Air and Oxygen Gasification
In this section, the results of equilibrium gasification numerical tests, carried out with air at atmospheric conditions (101 325 Pa and 298.15 K) as oxidizer, are presented and discussed.
The results obtained by air gasification are here compared with those of Prins et al. reference study, in which gasification at equilibrium had been operated by oxygen and steam. The reference paper indicates that, for the fuels with O/C < 0.4, gasification was carried out with the injection of steam at atmospheric pressure and 500 K temperature. Steam had the purpose to limit gasification temperature, which would rise to very high values for the low-oxygen content fuels at the carbon deposition boundary conditions.
The diagrams shown in the following have in abscissa the oxygen-to-carbon ratio of the tested fuel. As observed by Prins et al., the influence of O/C ratio on fuels gasification is predominant compared to that of H/C ratio. The tests were carried out for three system conditions:
- Carbon deposition boundary (CDB): it is the condition at which charcoal disappears from gasification products; CDB presents the maximum value of cold gas efficiency (syngas to fuel chemical energy content ratio) for the gasification process;
- 1200 K reaction temperature;
- 1500 K reaction temperature.
Tests at CDB
Figure 2 shows the Carbon Boundary Temperature (i.e. gasification temperature calculated by the model in the CDB conditions) diagram in function of the fuel O/C ratio. The diagram compares the results obtained by Prins et al. for oxygen-steam gasification (the two solid lines in the figure) with those obtained in the present work (the diamonds in the figure) for air gasification. The vertical distance between the two solid lines (oxygen-steam gasification), so as the vertical spread of the dots (air gasification), is due to the marginal influence of the fuels H/C ratio, as stated by Prins et al. publication of 2007.
- Oxygen-steam gasification results show a very high reaction temperature — exceeding 2500 K — for the low O/C fuels (coals), whereas for the fuels with a high O/C value (biomasses) the temperature tends to 1070 K.
- With air as oxidizer, coals gasification temperature is significantly lower as compared to oxygen-steam gasification; in biomass fuels gasification, reaction temperature is about 70-80°C lower than that of oxygen-steam case.
To understand why coals, in air gasification, reach very lower temperatures compared to oxygen-steam gasification, it is necessary to assess the role of nitrogen. Nitrogen contained in air constitutes a mass of inert gas absorbing reaction heat thanks to its thermal capacity. Being coals composition characterized by a low oxygen content, the amount of air required for complete gasification is higher than for biomasses. Therefore, the amount of nitrogen involved in coal gasification with air is considerable, determining a significantly lower reaction temperature than for oxygen-steam reactions. Instead, biomass needs less air to be fully gasified having about 40% oxygen content, thus the lower nitrogen mass involved in the reaction causes air gasification temperature to be closer to that of oxygen-steam gasification.
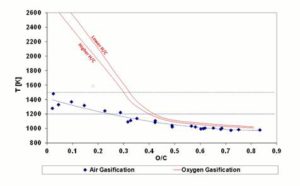
Figure 2: Temperature at CDB. Lines Indicate Oxygen — Steam Gasification; Diamonds Indicate Air Gasification. Air Gasification Results are Joined by a Dashed Polynomial Trendline
Figure 3 shows the diagram of global exergetic efficienciey  and chemical exergetic efficienciey
and chemical exergetic efficienciey 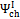 (Equations 5 and 7) versus the O/C ratio at CDB conditions.
(Equations 5 and 7) versus the O/C ratio at CDB conditions.
For oxygen – steam gasification, 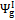 decreases monotonically with the O/C ratio from about 0.86 to about 0.78.
decreases monotonically with the O/C ratio from about 0.86 to about 0.78. 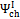 ( shows a maximum around O/C = 0.4; below this value, ΨchI drops because of the reaction products high physical exergy content, caused by the high reaction temperature; above O/C = 0.4, the
( shows a maximum around O/C = 0.4; below this value, ΨchI drops because of the reaction products high physical exergy content, caused by the high reaction temperature; above O/C = 0.4, the 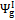 and
and 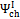 curves are substantially parallel, as reaction products thermal content is constant with increasing O/C ratio (see also the
curves are substantially parallel, as reaction products thermal content is constant with increasing O/C ratio (see also the 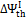 diagram in Figure 4).
diagram in Figure 4).
For air gasification, 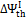 shows a monotonically increasing trend, exceeding the oxygen-steam chemical efficiency for an O/C ratio of about 0.5. This is explained observing that in oxygen — steam gasification, chemical exergy of the oxidizer in Equation (7) represents a net loss, whereas, for atmospheric air, the exergy of oxidizer stream is zero.
shows a monotonically increasing trend, exceeding the oxygen-steam chemical efficiency for an O/C ratio of about 0.5. This is explained observing that in oxygen — steam gasification, chemical exergy of the oxidizer in Equation (7) represents a net loss, whereas, for atmospheric air, the exergy of oxidizer stream is zero. 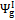 for air gasification slightly increases from coals to biomasses and exceeds that of oxygen – steam gasification for O/C = 0.5.
for air gasification slightly increases from coals to biomasses and exceeds that of oxygen – steam gasification for O/C = 0.5.
The last effect can be explained as a combination of 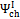 increase and of the
increase and of the 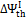 parameter behavior, representative of the physical exergy of the products stream.
parameter behavior, representative of the physical exergy of the products stream.
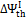 , shown in Figure 4, is higher for oxygen — steam gasification than for air gasification for the fuels with a low O/C ratio; instead, for biomass fuels (high O/C ratio) air and oxygen — steam gasification show equal and rather constant values of
, shown in Figure 4, is higher for oxygen — steam gasification than for air gasification for the fuels with a low O/C ratio; instead, for biomass fuels (high O/C ratio) air and oxygen — steam gasification show equal and rather constant values of 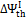 .
.
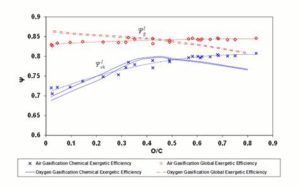
Figure 3: Exergetic Efficiencies at the CDB. Lines Refer to Oxygen – Steam Gasification; Diamonds and Crosses Indicate Air Gasification. Dashed (Polynomial) Trendlines Join Air Gasification Results

Figure 4: Δψthi, Parameter in Function of Fuel O/C Ratio. Gasifier Operating at CDB Condition
An analysis of the influence of the H/C ratio on exergetic efficiency leads to the observation that both global and chemical exergetic efficiencies increase with H/C ratio in gasification at CDB conditions.
Tests at 1200 K (927°C)
Figure 5 shows the exergetic efficiency diagram for 1200 K reaction temperature.
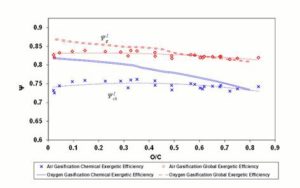
Figure 5: Exergetic Efficiencies at 1200 K. Lines Refer to Steam – Oxygen Gasification; Diamonds and Crosses Indicate Air Gasification. Dashed (Polynomial) Trendlines Join Air Gasification Results
Oxygen — steam gasification results show a decreasing trend of 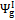 with the O/C ratio, and a similar trend is visible for
with the O/C ratio, and a similar trend is visible for 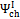 .
.
For air gasification, lower values of 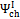 can be noticed compared to the oxygen — steam case. Air reaction chemical efficiency approaches oxygen — steam values for the highest O/C ratio fuels. Above O/C = 0.55,
can be noticed compared to the oxygen — steam case. Air reaction chemical efficiency approaches oxygen — steam values for the highest O/C ratio fuels. Above O/C = 0.55, 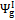 for air approaches the value found for oxygen — steam; consequently fuels with high oxygen content seem to be suitable for air gasification at 1200 K with an acceptable global efficiency.
for air approaches the value found for oxygen — steam; consequently fuels with high oxygen content seem to be suitable for air gasification at 1200 K with an acceptable global efficiency.
According to Equations 5 and 6, exergetic efficiencies 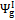 ,
, 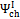 and , may assume different values if reaction products contain solid output, as happens at 1200 K conditions for the low O/C ratio fuels. In Figure 6 is reported the diagram of exergetic efficiencies, which show a peak near O/C = 0.1. This comes from the different definition of the global and chemical exergetic efficiencies
and , may assume different values if reaction products contain solid output, as happens at 1200 K conditions for the low O/C ratio fuels. In Figure 6 is reported the diagram of exergetic efficiencies, which show a peak near O/C = 0.1. This comes from the different definition of the global and chemical exergetic efficiencies 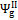 and
and 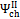 , presenting the charcoal exergetic content as a useful effect instead of a loss.
, presenting the charcoal exergetic content as a useful effect instead of a loss.
In Figure 7, the parameter , for 1200 K gasification temperature is diagrammed. As visible, 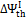 values for oxygen and air gasification result similar in the gasification of high O/C fuels; instead, for the low O/C fuels a difference of 4 — 5% of can be remarked between oxygen — steam and air gasification.
values for oxygen and air gasification result similar in the gasification of high O/C fuels; instead, for the low O/C fuels a difference of 4 — 5% of can be remarked between oxygen — steam and air gasification.
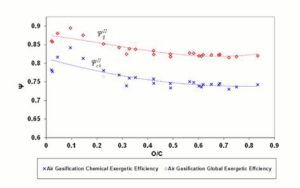
Figure 6: Exergetic Efficiencies Ψgii and Ψchii At 1200 K. Dashed (Polynomial) Trendlines Join Gasification Results
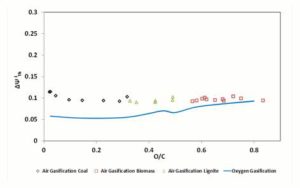
Figure 7: Δψthi Parameter in Function of Fuel O/C Ratio. Gasifier Operating at 1200 K Condition
The analysis of numerical results for 1200 K reaction temperature also shows that for the fuels showing H/C ratio lower than 1, exergetic efficiencies increase with H/C ratio; instead, for the fuels showing H/C ratio higher than 1, exergetic efficiencies decrease with H/C ratio.
Tests at 1500 K (1227°C)
Figure 8 shows 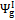 and
and 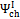 for 1500 K reaction temperature. For biomass fuels, gasification occurs closer to the stoichiometric combustion conditions, implying a lower chemical exergetic efficiency both for oxygen and for air reactions. In particular, air gasification presents low
for 1500 K reaction temperature. For biomass fuels, gasification occurs closer to the stoichiometric combustion conditions, implying a lower chemical exergetic efficiency both for oxygen and for air reactions. In particular, air gasification presents low  values for all the fuels, being operated at temperatures above the CDB.
values for all the fuels, being operated at temperatures above the CDB.
Finally, Figure 9 provides the trend of 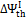 , for 1500 K reaction temperature. As visible in the diagram, the exergetic efficiency loss for air gasification keeps fairly constant to a value of 0.2, whereas for oxygen gasification it assumes resolutely lower values.
, for 1500 K reaction temperature. As visible in the diagram, the exergetic efficiency loss for air gasification keeps fairly constant to a value of 0.2, whereas for oxygen gasification it assumes resolutely lower values.

Figure 8: Exergetic Efficiencies at 1500 K. Lines Refer to Oxygen – Steam Gasification; Diamonds and Crosses Indicate Air Gasification. Dashed (Polynomial) Trendlines Join Air Gasification Results
At 1500 K gasification temperature, the H/C ratio increase has a negative influence on gasification exergetic efficiencies, which tend to decrease increasing H/C.
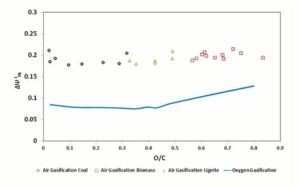
Figure 9: Δψthi Parameter in Function of Fuel O/C Ratio. Gasifier Operating at 1500 K Condition
Evaluation of Non — Equilibrium Exergetic Efficiency for Biomass Fuels
The results obtained through equilibrium modeling in the previous sections show that air gasification is advantageous over oxygen — steam gasification for biomass fuels at CDB and 1200 K reaction conditions. In the present section, the evaluation of exergetic efficiency for a real air gasification reaction is provided for the biomass fuels of Table 2, i.e. from Lignin Softwood on.
Description of the Modified Equilibrium Model
The complete description of the modified equilibrium model is given in the papers by Damiani and Trucco. In Figure 10 is represented the logical scheme of the modified model, including the correction factors which account for the main non-equilibrium effects. The feed — stream is divided into four streams: carbon, hydrogen, oxygen and nitrogen. As indicated in Figure 10, the carbon stream is first subtracted of the quantity 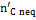 , representing the moles of solid carbon which appear in the products and which have not reached equilibrium.
, representing the moles of solid carbon which appear in the products and which have not reached equilibrium. 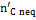 is found through Equation (10), once the coefficient δC1 is known.
is found through Equation (10), once the coefficient δC1 is known.
 (10)
(10)
Being 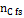 the number of moles of carbon present in the feed-stream.
the number of moles of carbon present in the feed-stream.
The quantity 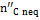 in Figure 10 is the carbon portion appearing in the products in the form of methane which has not reached equilibrium; this quantity is determined by Equation (11) through the coefficient δC2:
in Figure 10 is the carbon portion appearing in the products in the form of methane which has not reached equilibrium; this quantity is determined by Equation (11) through the coefficient δC2:
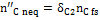 (11)
(11)
Since one mole of methane is composed by one mole of carbon and four moles of hydrogen, the H stream must be subtracted of a quantity of hydrogen  that is 4 times
that is 4 times  .
.
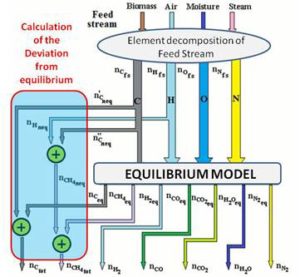
Figure 10: Scheme of the Modified Model Complete of Non-Equilibrium Correction
The value of correction coefficients δC1 and δC2 was derived from a model tuning, by means of an optimization process based on the comparison with the experimental data of Chern et al. (1991). Through this procedure, the δC1and δC2 coefficients were provided as functions of the Equivalence Ratio (ER = (A/F)/ (A/F) stochiometric).
To evaluate the effect of reactions non – equilibrium on the gasification of different biomass fuels, correction functions calculated by means of the modified model were applied to the equilibrium exergetic efficiencies ΨgI and ΨchI.
The correction functions are defined as the ratio between:
- The exergetic efficiency calculated through the modified equilibrium model for an average biomass fuel, having chemical formula CH1.503O0.681.
- The exergetic efficiency calculated for the same biomass fuel by means of the basic equilibrium model.
The ratios were calculated for ER ranging from 0.23 to 0.34, obtaining two correction functions for respectively the global and the chemical exergetic efficiencies:

Multiplying the values of ΨgI and ΨchI — previously found for the biomass fuels — by the values of Σg and Σch obtained through Equations (12) and (13), the gasification exergetic efficiencies for non — equilibrium reactions were calculated. The resulting efficiency curves are presented in Figures 11 and 12, where equilibrium and non – equilibrium exergetic efficiency values are compared. For each fuel, the non — equilibrium global and chemical exergetic efficiencies are the efficiencies obtained through a real gasification reaction carried out with the same ER of the ideal reaction. Of course the term CDB, having the definition provided at the beginning, loses of sense when real reaction occurs, since the products always contain solid charcoal. Also, for 1200 K tests, the reaction temperature out of equilibrium will not assume the constant value of 1200 K. However, for clarity, the acronym “CDB” and the label “1200 K” were here maintained.
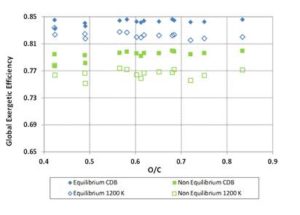
Figure 11: Global Exergetic Efficiency for Biomass Fuels. Comparison between Equilibrium and Non-Equilibrium Results for CDB and 1200 K Reaction Conditions
For the tests at CDB, the calculated values of the correction function Σg increase with O/C ratio from 0.935 to about 0.945; therefore the global exergetic efficiencies for real gasification get closer to the values calculated by the equilibrium model for the high oxygen content fuels; Σch, instead, keeps around 0.945 for all the fuels.
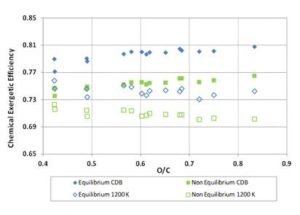
Figure 12: Chemical Exergetic Efficiency for Biomass Fuels. Comparison between Equilibrium and Non-Equilibrium Results for CDB and 1200 K Reaction Conditions
For the tests at 1200 K temperature, the values of Σg decrease from 0.955 to 0.945 with fuels O/C ratio increasing; the values of Σch increase from 0.93 to 0.94 with the fuels O/C ratio; therefore, the chemical exergetic efficiency of real gasification approaches that of ideal reaction for fuels with higher O/C ratio.
Conclusions
The present paper provided an exergetic analysis of the gasification reaction, focusing on the second principle conversion efficiency of different fuels. In particular, several fossil coals and biomasses were investigated, through a set of numerical tests carried out with an equilibrium model. The results with air as oxidizer were compared with the results of a reference work by Prins et al. focused on oxygen — steam gasification. The calculations were performed in three operating conditions: Carbon Deposition Boundary, 1200 K and 1500 K gasification temperature.
The results obtained show that, at CDB conditions, air gasification is advantageous from the point of view of global and chemical exergetic efficiency for biomass fuels. At 1200 K reaction temperature, global efficiencies for air and oxygen gasification are comparable for biomasses with O/C > 0.55. Chemical efficiency values are slightly lower for air than for oxygen-steam. Finally, at 1500 K reaction temperature, oxygen — steam gasification is more efficient than air gasification.
According to the results, air gasification may be considered as a suitable conversion process of solid fuel into combustible gas for the high O/C ratio fuels (biomasses); in order to maximize conversion efficiency, the reaction has to be controlled, maintaining an operating condition as close as possible to CDB, so that gasification may occur at the lowest temperature compatible with complete solid to gas conversion; in any case, air gasification reaction temperature should be kept lower than 1200 K, otherwise the efficiency advantages compared to oxygen — steam reaction will be lost.
Finally, a modified equilibrium model able to account for the main non — equilibrium effects of gasification thanks to the tuning on experimental data, was employed to give an idea of the exergetic efficiencies occurring in a real gasification reaction with air as oxidizer. The analysis carried out through the modified model was applied to biomass fuels.
It is dutiful to mention that, in case of air gasification, the syngas quality is lower than that obtained through oxygen gasification, for the massive presence of nitrogen in the producer gas composition. An evaluation is therefore required as a further step of the research, assessing for which real applications it is convenient not to produce oxygen (expensive process) while accepting a lower calorific value of the produced gas
The comparison between air and oxygen non — equilibrium exergetic efficiencies is an open issue and will be faced in future works.
Nomenclature
Abbreviations
CDB Carbon Deposition Boundary
ER Equivalence Ratio
F Fuel
fs Feed stream
Ox Oxidizer
Symbols
C Specific Heat Capacity for a Solid [kJ kmol-1 K-1]
cp Specific Heat Capacity for a Gas [kJ kmol-1 K-1]
Ex Exergy [kJ kmol-1]
ER Equivalence Ratio [-]
H/C Hydrogen to Carbon rati [-]
HHV Higher Heating Value [kJ kg-1]
LHV Lower Heating Value [kJ kg-1]
ni Number of Moles of ith species [kmol/kmol fuel]
O/C Oxygen to Carbon ratio [-]
p Pressure [Pa]
R Gas constant [kJ kmol-1 K-1]
T Temperature [K]
vm Solid Molar Volume [m3 kmol-1]
Greek Symbols
β LHV — to — Exergy proportionality term [-]
δ Non-equilibrium correction coefficient [-]
Ψ Exergetic Efficiency [-]
ΔΨTh Thermal Efficiency Loss [-]
Σ Efficiency correction function [-]
Subscripts
0 Related to the Reference State
ch Chemical
g Global
i ith gaseous compound
ph Physical
References
Baher, H. D. (1968). ‘On The Definition of Exergetic Efficiency, A Systematic Study,’ Brennstoff-Wärme-Kraft, 20 (5) 197-200.
Bejan, A., Tsatsaronis, G. & Moran, M. (1996). ‘Thermal Design & Optimization,’ Wiley Inter Science.
Google Scholar
Chern, S. M., Walawender, W. P. & Fan, L. T. (1991). “Equilibrium Modeling of a Downdraft Gasifier I — Overall Gasifier,”Chemical Engineering Communications, 108, 243-265.
Publisher – Google Scholar
Damiani, L. & Trucco, A. (2009). “Biomass Gasification Modelling: An Equilibrium Model, Modified to Reproduce the Operation of Actual Reactors,” Conference Proceedings of ASME Turbo Expo.
Publisher – Google Scholar
Damiani, L. & Trucco, A. (2010). “An Experimental Data Based Correction Method of Biomass Gasification Equilibrium Modeling,” Journal of Solar Energy Engineering, 132 (3).
Publisher – Google Scholar
Grassman, P. (1950). ‘On the Common Definition of Efficiency,’ Chemie Ingenieur-Technik, 22 (4) 77-80.
Google Scholar
Prins, M. J. & Ptasinski, K. J. (2005). “Energy and Exergy Analyses of the Oxidation and Gasification of Carbon,”Energy; 30, 982-1002.
Publisher – Google Scholar
Prins, M. J., Ptasinski, K. J. & Janassen, F. J. J. G. (2003). “Thermodynamics of Gas-Char Reactions: First and Second Law Analysis,” Chemical Engineering Science, 58 (13-16), 1003-1011.
Publisher – Google Scholar
Prins, M. J., Ptasinski, K. J. & Janassen, F. J. J. G. (2007). “From Coal to Biomass Gasification: Comparison of Thermodynamic Efficiency,” Energy, 32, 1248-1259.
Publisher – Google Scholar
Ptasinski, K. J., Prins, M. J. & Pierik, A. (2007). “Exergetic Evaluation of Biomass Gasification,” Energy 32 (4), 568-574.
Publisher – Google Scholar
Sato, N. (2004). Chemical Energy and Exergy: An Introduction to Chemical Thermodynamics for Engineers, Elsevier Science & Technology Books.
Publisher – Google Scholar
Szargut, J. (1989). “Chemical Exergies of the Elements,” Applied Energy, 32, 269-286.
Publisher – Google Scholar
Szargut, J. & Styrylska, T. (1964). ‘Approximate Evaluation of the Exergy of Fuels,’ Brennstoff Warme Kraft, 16 (12) 589-596.
Google Scholar
Wark, K. (1995). Advanced Thermodynamics for Engineers, McGraw-Hill.
Publisher – Google Scholar
www.anl.gov.
www.et.byu.edu
www.woodgas.com.






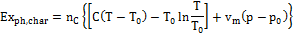

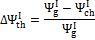 (9)
(9)














