Introduction
Forest and agro-industrial residues are materials of potential value as solid fuels. They must be easy to handle and have the least possible amount of moisture content.
Drying is an energy-demanding operation and therefore it is necessary to understand the supramolecular idiosyncrasies related to the migration of water in porous materials (dynamic porosity, that is the combined effect of porosity and of constrictivity and tortuosity of pores) [1].
Optimal combustion of biomasses also depends on their dynamic porosity [1]. Combustion occurs as the initial pyrolysis of the main bio-organic constituents. The resulting decomposition products react with each other and with oxygen in the air feed. Flames are due to combustion of the thermally produced gases and not by combustion of the solid fuel itself. Incomplete combustion gives rise to significant amounts of CO, hydrocarbons and tar that result in lower combustion heats and highly pollutant emissions. The entire combustion process, similar to other kinds of biomass thermochemical conversions (e.g. gasification and pyrolysis), is dependent on internal fluid diffusivity, which is closely related to the dynamic porosity of each material.
A straightforward method we recently published for the quantitative comparison of fluid diffusivity in porous solids [1] is now applied to the determination of the dynamic porosity of sawdust of different species to be considered as energy asset.
Qualitative discussion of the model
The method is based on the kinetic features of drying curves. Loosely-bound water located at particle surfaces evaporates according to zeroth-order kinetics because its vapour pressure remains constant during the time of total coverage of the surface. This constant kinetic regime holds for as long as water molecules arrive at the particle surface as fast as evaporation takes place. This constant rate is independent of the chemical nature of the substrate, and similar to the rate of evaporation of free liquid surfaces.
“Dry islands” on the surface eventually appear once a critical degree of drying is achieved (xc), and the rate now depends on the residual moisture content and the air-particle interfacial fluxional area. This second stage is due to H2O-substrate molecular interactions and internal transport limitations. A third stage is often observed at high degrees of drying, when the surface is dry and the evaporation plane slowly gets its way through the matrix up to the surface.
It is tenable that materials with higher xc values (longer constant-rate periods) correspond to high dynamic porosity. This issue has also been dealt with by Yiotis et al. [2] through 3-D-pore network model simulations and by Songok et al. [3] on the influence of coating on the drying of paper.
Thus, we present results on xc and specific effective fluxional area values for 14 types of finely ground saw dust studied at 50 °C. Kinetic results are also discussed as a criterion for energy-cost of drying.
Materials and methods
Materials
The samples were obtained from different sawmills in Costa Rica. Pinus caribea sample from La Chonta Sawmill, Cartago. The rest of materials were provided by Inmobiliaria MxM, Maderas Garabito, Maderas Fallas, and Corporación Agrícola Del Monte, all sawmills located in the province of Limón. They were air dried, reduced in size down to finely divided saw dust, and kept in sealed plastic bags.
Drying kinetics and data treatment
All experiments were carried out in laboratory environment kept at 60  5 % relative humidity and 87 kPa barometric pressure.
The solid samples were soaked overnight with tap water. Shortly before the gravimetric measurements, the materials were filtered out (Büchner funnel) and pressed between paper towels to obtain free-flowing solids.
10-g samples were spread loosely on the balance dishes, and mass loss monitored at 50 °C by using Ohaus MB35 Halogen Moisture Analysers. Crude mass — time data pairs were subjected to
linear least-square fitting for the set of numbers for which a linear correlation is significant with a r = 0.9990. The -dm/dt value corresponds to the initial rate of surface evaporation and the range of validity allows the calculation of xc. All experiments were carried out in triplicate. Additional runs were carried out when necessary.
The effective surface fluxional area of the samples was calculated from the initial constant rate and the previously determined rate of water evaporation at 50 °C and 87 kPa (11.37 mmol s-1 m-2).
All numerical results are given with the magnitude of a standard error from the mean.
Energy-cost of drying
It is possible to obtain energy-cost information from drying kinetics and the operation conditions of the moisture analysers. These instruments run at 110 V and consume 4 A [4].
Thus for a given experiment, the total electrical energy used equals to the amount 110 V ï‚´ 4 A ï‚´ time. The fraction of electrical energy actually used for the evaporation of water was obtained as the ratio of the evaporation thermal energy of M grams of water (M ï‚´ 2259 J g-1) to the total electrical input. M is the difference between the initial mass of the sample and the final mass of the dried sample. An empirical regression equation was obtained as a function of M:
Energy fraction = 1.091 ï‚´ 10-3 + 3.520 ï‚´ 10-4 M — 1.466 ï‚´ 10-5 M2
Since the heating power is constant and evaporation takes place against a stagnant gaseous surrounding (no significant haulage air currents), the thermal energy needed to achieve the various degrees of drying is solely dependent on the process kinetics.
Results and Discussion
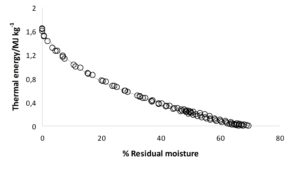
Drying kinetics. Figure 1 shows the kinetic profile for the drying process for the sawdust of Enterolobium cyclocarpum at 50 °C, 60 % relative humidity and 87 kPa. The data points correspond to three experiments combined. Note that the constant-rate (dx/dt) extends along the first quarter of the drying process.
Fig. 1. Drying curve of E. cyclocarpum sawdust at 50 °C, 60 % relative humidity and 87 kPa
Table 1 gives the xc and specific fluxional areas of the 14 samples studied. Except for the case of Lecythis ampla, no statistically significant difference was found amongst the 13 remaining biomasses. The mean xc value resulted equal to 0.26  0.03 (vs. 0.41  0.02, p < 0.01).
Table 1. xc Parameter and specific effective fluxional areas for the lignocellulosic biomasses at 50 °C, 60 % relative humidity and 87 kPa
This salient feature of L. ampla need not be considered surprising based on details of its anatomy that have been described in the literature [5, 7]. This species’ sapwood has a high number of vascular fibres and high density of wide vessels (mean diameter = 150 ïm). Its fresh wood is heavy (1.2 g cm-3 — 1.3 g cm-3) and contains a moisture content of 93 % – 96 %. Many of these anatomical features must still be present in the water-saturated sawdust.
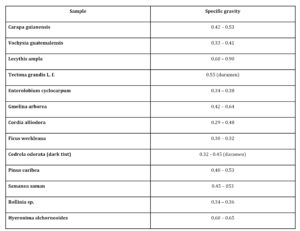
The specific effective fluxional areas were similar for all biomaterials (1.4  0.2 m2 kg-1), a feature we have found common for most lignocellulosic materials. Table 2 shows the specific gravity of the materials studied in this work.
Table 2: Specific gravity of different dry wood samples [5 — 8]
The specific gravity of dry L. ampla wood is greater than the mean value for the rest of the materials: 0.75 vs. a mean value of 0.44  0.09 (p < 0.01). High values of specific gravity are correlated with thicker xylem walls.
Drying energy cost. Data such as those in figure 1 can be transformed into energy-cost curves, according to the numerical procedure explained in section Energy-cost of drying. Thus, thermal energy is given to achieve different degrees of moisture reduction. The case of E. cyclocarpum is shown in figure 2.
Fig. 2. Energy cost for drying E. cyclocarpum sawdust at 50 °C, 60 % relative humidity and 87 kPa
All samples give similar values of slope during the first constant-rate stage, as expected from the molecular interpretation of the drying process discussed in the introduction.
Table 3 gives the drying-energy cost for the samples at x = xc and x = 1. The ratio Ec/E1 is the fraction of thermal energy needed to achieve xc (superficial evaporation). The amount 1 — (Ec/E1) is more useful because it gives the fraction of drying energy needed to promote water evaporation during the decreasing-rate stage, when effects other than water volatility control the process: matrix porosity and pore constrictivity and tortuosity.
Table 3: Drying energy for the different sawdust samples at 50 °C, 60 % relative humidity and 87 kPa
Water evaporation from L. ampla sawdust (xc = 0.41) shows lower energy requirement to cope with the biomass internal transport features than the other 13 cases: 0.76  0.03 vs. a mean of 0.87  0.03 (p < 0.01). For the decreasing-rate period, an empirical regression equation can be obtained as suggested by the plotting of the data in figure 3:
(1 — Ec/E1) = (1.07  0.01) — (0.79  0.05) xc
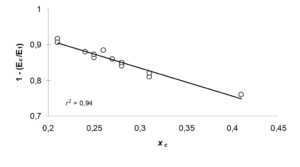
Fig.3: Effect of dynamic porosity on the fraction of energy needed for the drying of sawdust samples at 50 °C, 60% relative humidity and 87 kPa
The physical meaning of this empirical correlation is immediate. The easier water diffusivity is in a given matrix, the lower energy requirement is needed to dry the material.
The results obtained could be considered to improve the management required for the use of forest biomasses. In this regard, a key issue is the supply chain optimisation which allows their transportation at lower cost, from the production place to the processing facility. Properties of lignocellulosic materials such as density and water content are fundamental elements to consider. In addition, a good understanding of the concept of dynamic porosity can lead to a better management of biomass in terms of economic efficiency and energy efficiency.
Moreover, measurements related with drying kinetics of forest biomasses represent a useful tool to decide about their pretreatment for a latter use. On this matter, information about dynamic porosity and specific fluxional area obtained from this simple methodology is valuable by itself, but can be also a great complement to more traditional information including chemical composition, cellulose crystallinity and degree of polymerization, particle size, pore size density and calorific power, amongst others.
Conclusions
The results justify the use of the dynamic porosity methodology as a tool to compare the drying energy requirements of porous materials, e. g. forest biomassses.
The methodology is simple to perform and allows understanding of macroscopic processing features, in terms of supramolecular idiosyncrasies of materials.
Acknowledgements
The authors thank the interest and advice of Prof. Eugenia M. Flores-Vindas. Mr. Ed Duran, Ohaus Corporation service manager provided useful information on the operational details of the moisture analyser used in this work. The work was done under the scientific cooperation agreement between the Korean Forest Research Institute (KFRI) and the Tropical Agricultural Research and Higher Education Centre (Catie). JFM-S thanks for his involvement in this project.
References
1. Ulate-Segura, D. G.; Mata-Segreda, J. F. (2014). “Drying kinetics as a method for the evaluation of relative diffusivity of water in porous biomass materials”, International Journal of Renewable Energy & Biofuels Vol. 2014 (2014), Article ID 970016, DOI: 10.5171/2014.970016.
2. Yiotis, A. G.; Tsimpanogiannis, I. N.; Stubos, A. K.; Yortsos, Y. C. (2006). “Pore-network study of the characteristic periods in the drying of porous materials”, Journal of Colloid and Interface Science 297, 738-748.
Publisher – Google Scholar
3. Songok, J.; Bousfield, D.; Ridgway, C.; Gane, P.; Toivakka, M. (2012). “Drying of Porous Coating: Influence of Coating Composition”, Ind. Eng. Chem. Res. 51, 13680−13685.
Publisher – Google Scholar
4. Instruction manual MB35 moisture analyzer. Ohaus Corporation, 19A Chapin Road, Pine Brook, NJ 07058-2033, USA.
5. Lens, F.; Bass, P.; Jensen, S.; Smets, E. (2007). “A search for phylogenetically informative wood characters within the Lecythidae S. L.”, American Journal of Botany 94 (4), 483-502.
Publisher – Google Scholar
6. Flores, E.M. (2002). “Lecythis ampla Miers” In: Vozzo, J. A. (ed.). Tropical Tree Seed Manual. Agricultural Handbook 721. Washington: Forest Service, United States Department of Agriculture. p. 540-543.
7. Flores-Vindas, E.; Obando-Vargas, G. (2015). Lecythis ampla Miers. In: Arboles del trópico Húmedo. Valor socioeconómico. 2nd Ed., Editorial Tecnológica de Costa Rica, Cartago, Costa Rica, pp. 497-503.
8. Flores, E. M. 2002 Samanea saman (Jacq.) Merrill. In: Vozzo, J. A. (ed.). Tropical Tree Seed Manual. Agricultural Handbook 721. Washington: Forest Service, United States Department of Agriculture. pp. 701-704.