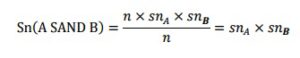Introduction
In health technology the final goal is divided into diagnosis, treatment and prevention. One of the most important objectives is the early diagnosis of the disease in the society which is collect screening. Screening is, in fact, the active way of looking for patients who do not seem to have major medical problems. It is performed via rapid laboratory tests, physical examinations or other methods (1).
Screening was defined in 1988 by the international committee of screening in England (2). Cost- benefit assessment is of a great importance in screening, and since it is usually implanted in large scale, it can have both benefits and also considerable costs to the society. This is true especially for the important diseases in the health care system.
Screening is performed for all or for those at high risk. Screening is done for diseases which are serious, curable and have a preclinical period during which early diagnosis is possible. Also, the window’s period before the triggering agent can lead to the illness should be long enough, early treatment has to give the way to better prognosis, and the prevalence of the disease must be high.
On the other hand, a good screening test should have good sensitivity and specificity, it must be rather safe, tolerable for the patient, and also impose low cost on the individual and the society. (3)
If a patient has the characteristics mentioned above, and a screening test has the required sensitivity and specificity, we still face a question:
Whether to perform the screening or not to implant, it needs quite a lot of investigations and researches to prove the effectiveness of the screening in the populations. These researches should be in the form of a large clinical trials; however, the studies done are very limited and with a lots of ambiguities in the forms of cohort or case- control studies.
There are many problems in screening; one of which is the false positive. False positive can lead to significant economic and psychological damage to the individual and society even if its rate is very low; because screening is usually done in large scale. (4)
Screening tests can include only one test, where a test with high sensitivity and specificity is performed, but they usually include several phases where one test is run to find the presumed patient, and then another test is done to prove the illness in that patient. In double- phase screening, it is very important how to combine the diagnostic tests.
In most text books and articles in epidemiology, it has been recommended to use the easier test for the first phase in the beginning, and then move on to a more accurate one with higher sensitivity, and specificity for those diagnosed positive in the first test (5). In this article, we aim for comparing the mixed tests by mathematical analysis based on final sensitivity and specificity, and to verify the order of the tests with different sensitivities and specificities, and their impact on the final specificity and sensitivity of the mixed test.
Mixed tests are performed either “in series” where the result of the first test determines whether to run the second test or not; or “in parallel” where, despite in series where the sequence of the tests is important, the second test is independent of the first one, and independently performed regardless of what the first test result is, and both tests are done at the same time.
The second aspect of mixed tests is “AND “or “OR”. In “AND” form, we consider the screening result positive if the result of both of the tests is positive. In “OR” form, only the positive result of one test is enough to consider the screening test positive.
Taking into account the mentioned items, we face at least seven mixed forms:
Series mixture of A “AND” B (A SAND B)
Series mixture of B “AND” A (B SAND A)
Series mixture of A “OR” B (A SOR B)
Series mixture of B “OR” A (B SOR A)
Parallel mixture of A “OR” B (A por B)
Parallel mixture of B “OR” A (B por A)
Parallel mixture of A “AND” B (A PAND B)
Now we verify each of the methods individually to find out how different methods can affect the find sensitivity and specificity.
A SAND B
In this test, test A is performed first and test B in only run if test A is positive, and the final positive patients are those who have both test A and test B are positive.
Now we calculate sensitivity and specificity of A SAND B in an accumulative way:
If we have a population of N people where the prevalence of the disease for screening is P, n= N×P, N is the number of patients in this society. For screening, we use the combination of test A “AND” B in series. In this way, snA is test A sensitivity, and spA is test A specificity, and test B has also snB (sensitivity), and spB (specificity).
In this test, running test B relies on test A result, and we consider an individual with both test A & test B positive results as a patient.
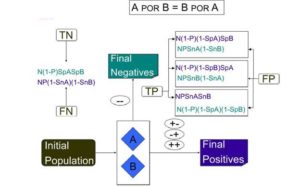
If test A is performed first, the number of people diagnosed as patients by this test is n×snA. On the other hand, healthy individuals diagnosed mistakenly as patients by this test is: (N-n) ×(1- spA). These people enter the second phase of screening having been positive for test A, on the other hand (N-n) × spA are the healthy people correctly diagnosed as healthy, and n-(n × snA) are the patients having the illness but incorrectly diagnosed as healthy. These patients are the ones with final negative screening results.
Those positive A test patients enter the second phase for test B. (n×snA)×snB are the real positive ones, and [(N-n)(1- spA)] × (1- spB) are the false positive ones of test A who will be diagnosed as patients by test B.
Also, in test B, (n × snA) — [(n × snA) × snB] are those real first test positive ones who will be incorrectly diagnosed as healthy; and [(N-n) × (1- spA)] × snB] are those false positive ones of test A who will be correctly diagnosed as healthy, and will be categorized as negative in the final screening result .
Finally, (n× snA) × snB are the real positive ones, and [(N-n) × (1-spA)] ×(1-spB) are the final false positive ones in the screening.
Also, [(N-n) ×spA] + [(N-n) × (1- spA)] × spB are the real negative ones and [n-(n× snA)] + [(n× snA) (1-snB)] are those with false negative results.
Sensitivity is the proportion of real patients who have been correctly diagnosed as patients:
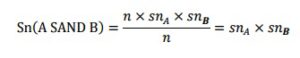
Specificity is the proportion of healthy individuals who have been correctly considered healthy.

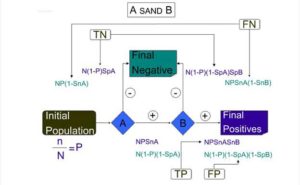
Figure 1: Shows Expressions in this Test, Test A is Performed First and Test B in Only Run if Test A is Positive, and the Final Positive Patients are Those Who Have Both the Test A and Test B are Positive.
B SANB A
In this method, test B is performed first, and test A is only performed if test B result is positive, and the final positive patients are those who have both test B and test A are positive.
Now we calculate sensitivity and specificity of B SAND A in an accumulative way:
If we have a population of N people where the prevalence of the disease for screening in P, n=N× Pn is the number of patients in this society. For screening, we use the combination of tests B “AND” A in series. In this way, snA is test A sensitivity, and spA is test A specificity; and the test B has also snB (sensitivity) and spB. (specificity).
In this test, the running test A relies on test B result, and we consider an individual with both tests A & B positive results as a patient.
If test B is performed first, the number of people diagnosed as patients by this test is n × snB. On the other hand, healthy individuals diagnosed incorrectly as patients by this test are: (N-n) × (1- spB). These people entered the second phase of screening having been positive for test B. On the other hand, (N-n) × spB are the healthy people correctly diagnosed as healthy, and n-(n× snB) are the patients with the illness but incorrectly diagnosed as healthy. These patients are the ones with final negative screening results.
Those positive B test people enter the second phase for test A. (n× snB) × snA are the real positive ones, and [(N-n)(1 – spB)] × (1 — spA) are the false positive ones of test B, who will be diagnosed as patients by test A.
Also in test A, (n × snB)-[(n× snB) × snA] are those real first test positive ones who will be incorrectly diagnosed as healthy; and [(N-n) × (1 – spB)] × spA are those false positive ones of test B who will be correctly diagnosed as healthy, and will be categorized as negative in the final screening result.
Finally, (n × snB) × snA are the real positive ones and [(N-n) (1 — spB)] × (1 – spA) are the final false positive ones in the screening.
Also, [(N-n) × spB] + [(N-n) × (1- spB)] × spA are the real negative ones, and [n-(n× snB)] + [(n× snB) (1-snA)] are those with false negative results.
Sensitivity is the proportion of the real patients who have been correctly diagnosed as patients:
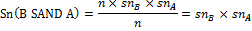
Specificity is the proportion of healthy individuals who have been correctly considered healthy.
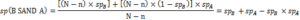
So far, we conclude that if only sensitivity and specificity are to be considered, when there are two tests with different sensitivities and specificities, it does not make any difference if we do any of the two tests first if the two tests are “in series” and “AND” form.
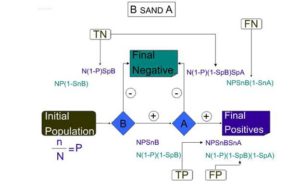
Figure 2: Shows Expressions in this Test, Test B is Performed First, and Test A is Only Performed if Test B Result is Positive, and Final Positive Patients are Those Who Have Both, Test B and Test A are Positive.
A SOR B
This method is a series mixture of two tests A “OR” B, and we only need one of the tests positive to consider the whole screening test as positive.
If test A is performed, the people diagnosed as patients by this test are n × snA. On the other hand, the healthy individuals diagnosed incorrectly as patients by the test is (N-n) × (1- spA), and because of “OR” of A and B tests in this method, they will be categorized as final positives in the screening. On the other hand, (N-n) × spA are of the healthy people correctly diagnosed and n (1- snA) of the patients will be incorrectly diagnosed as healthy, and enter the second phase of screening.
Of those false negative ones in test A, n(1- spA) ×snB will be correctly diagnosed as positive in test B, and of those real negative ones [(N-n) spA] × (1- spB) will be incorrectly diagnosed as false positive, and these will be considered on the final positives in the screening. Thus, n(1- snB) × snA of those false negatives have been identified; and of those real negative ones [(N-n) spB] × spA will have a test B negative result and will be in the final negatives in the screening.
Hence, [n × snA + n (1- snA)] × snB is the real positive number, and [(N-n) × (1- snA)] + [(N-n) ×spA (1- spB) is the false positives of this screening.
The real negative ones are (N-n) ×spA× spB, and the false negative ones is n× (1- snA) × (1- spB).
Finally, sensitivity is the real patients which are the proportion of real positives to all patients:
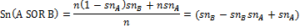
Specificity is the proportion of healthy individuals correctly diagnosed as healthy:
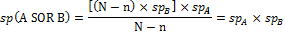
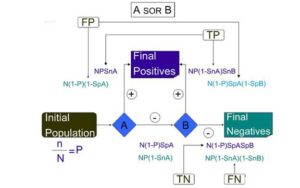
Figure 3: Shows the Expressions in this Method as a Series Mixture of Two Tests A “OR” B, and We Only Need One of the Tests Positive to Consider the Whole Screening Test as Positive
B SOR A
This method is a mixture of two tests B “OR” A. and if only one test is positive or both tests are positive, we consider the individual as patient.
If test B is performed first, true positives are n × snB. On the other hand, the healthy individuals diagnosed incorrectly as patients by the test are (N-n) ×(1- spB), and because of “OR” of A and B tests in this method, they will be categorized as the final positives in the screening. On the other hand, (N-n) × spB of healthy individuals correctly and n× (1- snB) of patients will be incorrectly diagnosed as healthy, and enter the second phase of screening which is test A.
Of those false negative ones in test B, n× (1- spB) × snA will be correctly diagnosed as positive in test A, and of those true negative ones [(N-n) ×spB] × (1- spA) will be incorrectly diagnosed as false positive, and these will be considered as final positives in the screening.
Therefore, n (1- snA) × snB of those false negatives have been identified; and of those true negative ones [ (N-n) spA ] × spB will have a test B negative result, and will be in the final negatives in the screening. Therefore, true positive of the screening is [n× snB + n (1- snB)] × snA, and the false positives of this screening is [(N-n) (1- spB)] + [(N-n) spB (1- spA)].
The real negative ones are (N-n) × spB ×spA and false negative ones is n× (1- snB) (1-snA).Finally, sensitivity is the real patient which is the proportion of real positives to all patients:

Specificity is the proportion of healthy; individuals correctly diagnosed as healthy:
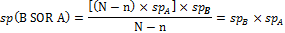
The results are similar to the previous method. It means in the “OR” method there is no difference in the final sensitivity and specificity of the screening test if we do either test first.
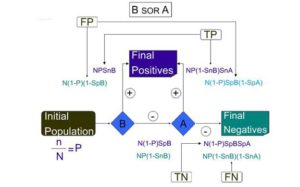
Figure 4: Shows that the Expressions in this Method are Mixture of Two Tests B “OR” A. and if Only One Test Is Positive or Both Tests are Positive, We Consider the Individual as a Patient
A PAND B = B PAND
A parallel mixture of two tests:
In the series screening, performing the second test depends on the result of the first test, while in the parallel mixture the two tests are performed at the same time. So, the sequence of the tests is not of an issue in tests; we need both of the tests positive, to declare the screening result as positive.
If the results of both tests are positive, the individual is regarded as the final positive of the screening. Of these positive cases, n × snB × snA are real positives, and (N-n) × (1- spA) ×(1- spB) are false positives. And the sum of these two makes the final positive in this screening.
On the other hand, if test A is negative and test B is also negative, (N-n) ×spA ×spB is the number of real negatives, and n× (1- snA ×(1- snB) is the number of false negatives in this screening.
If test A is positive and test B is negative, n× snA × (1- snB) is the number of false negatives and (N-n) × (1- spA) × spBis the number of real negatives.
If test A is negative and test B is positive, n× snB × (1- snA) is the number of false negatives and (N-n) × (1- spB) ×spA is the number of real negatives. Therefore, the number of all the real negatives in this screening is:
[(N-n) spA spB +(N-n)(1- spA) spB + (N-n)(1- spB) spA ] and the sensitivity of this mixed screening is the proportion of real positives diagnosed by this screening to all patients in society:
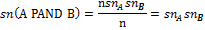
Specificity is the proportion of real negatives of the screening to the healthy individuals of the population:
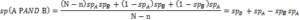

Figure 5: Shows that the Expressions in the Series Screening, Performing the Second Test Depend on the Result of the First Test, while in Parallel Mixture the Two Tests are Performed at the Same Time
A POR B = B POR A
The Parallel mixture of two tests, if the two tests are performed at the same time, and one or both of the tests are positive, the individual is regarded as a patient. And because of its parallel nature, the sequence is not important in this screening and both mixtures are equal. In this mixed (combined) screening, if both tests are negative, the individual is considered as a healthy. But if one or both of the tests are positive, the person is considered as the final positive.
If both tests are negative (N-n) spA spB of the real healthy individuals are correctly diagnosed as healthy. And n (1- snA) (1- snB) are false negatives.
On the other hand, if test A is positive and test B is negative, (N-n) (1- spA) spB will be the false positive and n snA (1- snB) will be the real positive cases.
If test A is negative and test B is positive, (N-n) (1- spB) spA will be false positive and n snB (1- snA) will be real positives and if both tests are positive, n snA snB will be real positive and (N-n) (1- spA) (1- spB) will be false positive. Thus, the number of total real positive cases in this combined screening is:
[N snA snB + n snA (1- snB) + n snB (1- snA)]
and a total real negative of this screening is: (N-n) spA spB. Finally sensitivity of A POR B is:
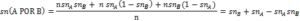
Specificity is:
Figure 6: Shows the Expressions in Parallel Mixture of Two Tests, if the Two Tests are Performed at the Same Time and One or Both of the Tests are Positive, the Individual is Regarded as a Patient
Result
We could proved by mathematical calculations that in none of the combining tests, the final sensitivity and specificity is affected by the sequence of the tests, and it does not make any difference, whether the more sensitive test is run first or the more specific one. But the amount of the intermediate false positive is affected by the sequence of the tests, and if the first test is more sensitive, we will have more false positives after the first test. Therefore, the type of the screening we choose relies on what our aim is for doing that screening.
Conclusion
Combined tests are either “in series”, where performing or not performing the second test depends on the first test result; or “in parallel” where, despite series form, the second test is independent of the first one and both tests are run concomitantly.
In the screenings, it is recommended to use “AND” methods if the aim is to enhance the final sensitivity of the test. However, “OR” methods are usually used if the target is to enhance the final specificity of the test. In none of the “series” or “parallel” mixtures, the sequence of the tests does not affect its final sensitivity and specificity. So, it does not make any difference whether to do the more sensitive test first or the more specific one.
But the rate of intermediate false positive results of these combinations is affected by the sequence of the tests, and if the first test is more sensitive, the false positive rate after the first test will be higher.
Therefore, choosing the type of screening test depends on the aim of that screening, and a combination of the tests should be selected, so that the test proves acceptable in terms of false positive rates; the harm to the patient coursed by the test, and also the cost imposed on the society. However, whether to do the more sensitive or specific test first, does not impact the final sensitivity and specificity of the screening.
References
1- Park, K. (2005). ‘Park’s Textbook of Preventive and Social Medicine,’ 18th edition, M/s Banarsidas Bhanot Publishers, India, 2005.
Google Scholar
2- (1998). “First Report of the National Screening Committee. Chapter Two: Definitions and Classification of Population Screening Programs,” London: Department of Health; 1998.
Publisher
3- Fletcher, R. H. & Fletcher, S. W. (2005). Clinical Epidemiology, The Essentials, Lippincott Williams & Wilkins, 4th edition, 2005.
Publisher – Google Scholar
4- Marteau, T. M., Cook, R., Kidd, J. et al. (1992). “The Psychological Effects of false-positive results in Prenatal Screening for Fetal Abnormality: A Prospective Study,” Prenatal Diagnosis 1992;12:205-214.
Publisher – Google Scholar
5- Gordis, L. (2004). Epidemiology, Third Edition, c2004
Publisher