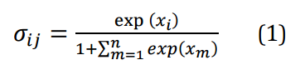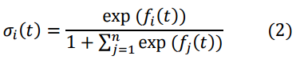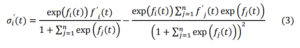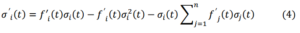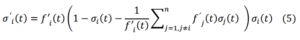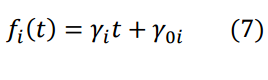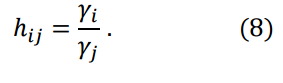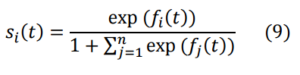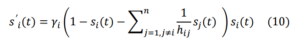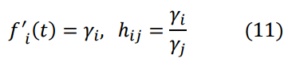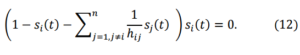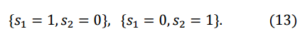Introduction
Mergers take place in a highly variable environment and the individual’s opportunity to learn the regularities of such environment are limited, due to the mid/long-term time horizon of the predictions. In such low validity situations, experts’ judgments tend to be greatly influenced by biases, if not properly aided by quantitative tools (Kahneman and Klein 2009). However, static models used in the recent years (See e.g. Werden and Froeb 1994; Epstein and Rubinfeld 2002; Werden and Froeb 2002) do not address the relevant question of the mid/long term effects of a merger, leaving authorities with limited support. The aim of this work is to develop a new mathematical model based on differential equations that might ameliorate some of the typical problems characterizing the quantitative analysis of mergers. The balance of this article is organized as follows: Section 2 offers a brief overview of the literature. Section 3 shortly presents the very well-known Antitrust Logit Model (ALM). Section 4 describes how the model proposed was generated and its strong link with the ALM. Section 5 offers a description of the model with market shares as the main variable and how it could be based on the PCAIDS model. Section 6 describes the model with prices as the main variables. In Section 7 there are some conclusive remarks.
A Brief Overview of the Literature
Merger control is possibly the most complicated challenge that antitrust authorities have to face. Unlike abuse of dominant position and cartel investigations, merger evaluation is exclusively forward looking; therefore, in addition to the typical intricacies of antitrust cases, the unavoidable uncertainty of medium/long term predictions has to be considered. In order to support antitrust authorities in this challenging task a plethora of mathematical models has been developed in the past two decades. There are multiple reasons behind the diffusion of merger simulation models (MSM) (Baker and Rubinfeld 1999). In the first place, there have been significant theoretical advancements and the computation potential became much greater. Secondly, unilateral effects from horizontal mergers have gained the spotlight, while at the same time the importance of potential efficiency gains is now widely recognized. To perform a comparison between unilateral effects and efficiency gains quantitative tools are fundamental. Lastly, there is much more data available to develop simulation models.
In spite of some attempts (Bergeijk and Kloosterhuis 2005), there is no universally accepted taxonomy of quantitative models; following Budzinski and Ruhmer it will be adopted a two-stage classification (Budzinski and Ruhmer 2010). According to Crooke et al., (Crooke et al., 1999) a merger simulation model lies on three crucial assumptions: the form of market interaction, the shape of marginal cost curves and the characteristics of demand. Consequently, at the first level Budzinski and Ruhmer identify three different kinds of models: Betrand models, Cournot models, and auction and supply function models. It is important to underline how the choice among them usually depends on the characteristics of the market and on the data available. Betrand models tend to be preferred in case of heterogeneous products, while Cournot models are usually adopted in homogeneous oligopolies (Kaplow and Shapiro 2007; Froeb and Werden 2008). Auction models instead are employed when the process leading to products sale is similar to that of an auction. At a second stage Bertand models are divided depending on the chosen demand form (Linear and log-linear, discrete choice demand, AIDS and PCAIDS, and multi-level demand estimation). What is crucial however is that these models do not consider the variable time and in fact “in the past empirical analysis of horizontal mergers has relied exclusively on static models” (Benkard et al., 2010).
Antitrust Logit Model
Among the models proposed to study the effect of mergers, one of the most popular is surely the Antitrust Logit Model (ALM), developed by Werden and Froeb (Werden and Froeb 1994). The ALM follows the classic scheme: analysis of supply, analysis of demand and identification of the equilibrium by crossing supply and demand. The analysis of the demand is based on the following ratio:

Where n is the number of firms and the variable xi used as exponent denotes that the proof offered in the following section is valid for any given exponent. There is therefore no need to introduce a specific demand function as the proof is valid for the most general case.At the numerator there is the “score” of the ith firm and at the denominator there is the sum of the scores of all the n firms operating in the market. It is important to underline how this ratio, and only this ratio, captures competitive interaction among firms. In fact, if the numerator of σij increases, the denominator of all the ratios will increase as well. Conversely, the supply side analysis, being based mainly on factors related to marginal costs, does not directly express the competitive interaction among firms. Crossing supply and demand is possible to identify the new equilibrium price, and consequently the price increase caused by the merger. As stated above, like most models developed to predict the effect of mergers, the ALM is a static model; therefore it attempts to predict the possible price increase by comparing the pre-merger static equilibrium with the post-merger static equilibrium.
Merger assessment, however, revolves around the potential medium term effects, while static models offer an answer of a different nature. To assume that firms set their prices according to Static Nash equilibria, instead of determining them taking into account complex dynamic behaviors, overlooks the role of competition to promote allocative efficiency, innovative efficiency, adaptive efficiency, consumer sovereignty, and economic freedom (Boudzinski 2004). Furthermore, to study a variable that is not dependent on the time makes it very hard to test the models ex-post. In fact it has been argued that the ex-post evaluation of MSM by a comparison of predicted and actual outcomes is still in its infancy (Ashenfelter and Hosken 2008).
To develop a model based on differential equations might improve the overall picture. In the first place, to study the stability and the structural stability of the model offers a measure of the reliability of the predictions, therefore helping to identify when it is possible to lessen the gap between the standard of proof required by the courts and the unavoidable uncertainty of mathematical predictions. More importantly, the solution of such dynamic model would describe the evolution of the main variable over time, offering an answer that is more in line with the interrogatives raised by merger evaluation. The question is then which model should be developed. Prominent scholars like Werden and Froeb, decided to describe the competitive interaction among firms through the abovementioned function, and it is easy to notice that the function is very similar to the function-solution of the traditional logistic model based on differential equations; therefore it appears to be a reasonable starting point.
Generation of a Competition Model Starting from the Antitrust Logit Model
As announced in the previous section, the analysis moves from the function used to describe the demand in the ALM. The idea is to propose a dynamic model whose solutions are as close as possible to the function used in the ALM to describe the competitive interaction among firms. Specifically, in the ALM the competitive interaction among n firms is taken into account analyzing the demand through the use of the following function:
It is easy to see why this ratio captures the competitive interaction among firms: if the numerator of σij increases, the denominator of all ratios relative to the remaining firms will automatically increase.
From now on, we assume that the value of all the quantities (1) could change over time. Furthermore, instead of the specific function (1), we consider the following more general function:
This reduces to (1) when the quantities are supposed to be independent on time. The derivative of this function is:
and taking into account (2), we finally obtain:
In conclusion, the functions (2) satisfy the following system of ordinary differential equations:
for j=1,…,n. This system assumes the form of a standard competition model:
provided that we choose functions f_i (t), linearly depending on time:
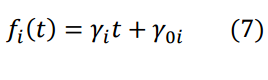
and introduce the notation:
In formulae (7) and (8) the quantities γi,γ0i,hij are constant.
We remark that for any choice of the functions fi (t) we still obtain a solution of the equation (4) which describes a more general competition model. In other words, we have proven that there is a competition model whose solutions belong to the family of functions used in the ALM. Consequently, the competition model based on differential equations presented in this section is coherent with the approach of the economists that have developed the ALM. In other words, the ALM is the other side of the coin of competition models based on differential equations. In concluding this section, we note that our approach exhibits the remarkable advantage to supply the solution of the complex non-linear system of differential equations underlying the competition model, thus, simplifying the analysis of its behavior.
Since the explicit solution of the competition model is now known, assigning and calibrating the parameters for this dynamic model is no longer more complex than for a static model. In fact, any model based on differential equations admits infinite evolutions compatible with equations. In order to choose one of the possible evolutions, we have to assign the initial data. This is exactly the same task economists have to perform when calibrating a static model.
A Model with Market Shares
We present two possible applications of the model described above. In this section we will discuss homogeneous oligopolies, and we will thus assume the existence of competition à la Cournot. Let F1,…, Fn be n firms competing in the same market and denote by s1, …, sn their relative market shares. In the view of their meaning, it is 0≤ si ≤ 1 and . All these conditions are verified by the functions (2). Changing our notation we obtain:
that we have shown to satisfy the following system of ordinary differential equations
where
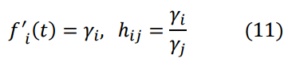
Since the above equations describe a competition model, it is natural to assume that γi represents Fi inner strength, whereas hij represents the competition coefficient relative to the pair Fi, Fj. To give these terms an economic meaning they can be translated in the familiar concepts of market power and competitive pressure. To assign a value to the parameters, it might be necessary to run an accurate investigation of the merger, yet this is conflicting with the need for screening devices for “quick looks” by enforcement agencies and by merging firms. However, Epstein and Rubinfeld show how PCAIDS allows to quickly obtaining a reasonable approximation of firms price elasticities (Epstein and Rubinfeld 2002). It is in line with mainstream theories to use price elasticity as a proxy for the inner strength (market power) of a firm. The last point to address is how to convert the information on market shares and demand elasticity in terms of price. The most straightforward approach is to determine the mark ups by dividing market share at any given time by the relative demand elasticity (Tschantz et al., 2000: 204).
It must be underlined that to remain coherent with the function used to describe the competitive interaction in the ALM firms’ competition coefficients will be dependent only on their inner strength. More specifically the competition coefficient of firm Fi with regards to firm Fj will be equal to the ratio of firms’ inner strengths. The consequences of these limitations will be highlighted shortly. In order to understand the characteristics of the model proposed, it is important to analyze the equilibrium positions that are the solutions of the algebraic system obtained by equating to zero the right hand side of the equations (10) that is,
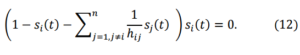
For the sake of simplicity we refer to the case n = 21. In such a case we obtain the following acceptable equilibrium solutions
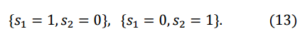
| 1 Considering more firms would not affect the outcome. |
These solutions show that the only possible equilibrium states are when one firm conquers the whole market in the long run2. This is caused by the strong link between the competition coefficient and the inner strength of the firms. We note that we introduced this link to propose a dynamic model that admitted function (1) as a solution. The above result shows that to describe a market in which more firms coexist, we have to generalize the model and abandon the restriction imposed by the artificial connection with ALM. It is easy to modify the model lessening this link, even if the price to pay is to resort to a numerical analysis of the differential system.
| 2 There is another equilibrium if both companies disappear from the market. |
In any case, the outcomes of these screening devices are not to be taken literally as they do not aim at predicting with precision the future state of the world. Their purpose is to help separating mergers necessitating a closer look from the ones that do not raise anticompetitive concerns. The crucial information that the proposed model can offer, is the comparison between the speed at which the solution reaches its equilibrium post merger and absent the merger, since it can be interpreted as the competitive advantage gained by the firm over its competitors, after the removal of the competitive constraint constituted by the merged firm. Whenever the merger might raise some concerns the results of this model should not be read alone, but combined with the results of the model proposed in the following section. There are at least four reasons to not overlook this model:
1.The computational burden is not larger than the one of static models, as the tasks to be performed and the data required are basically identical. At the same time it offers answers that are more in line with the interrogative raised by merger assessment.
2.What happens when t tends to infinity holds very little relevance. As stated above, the outcomes of quick screening devices are not to be taken literally. In any case, if firms are forced to compete forever without external shocks, the prediction that sooner or later only one will survive does not appear so absurd. More importantly, this model underlines that if we consider the function used in the ALM as dependent on the time it inevitably predicts the creation of a monopoly.
3.It is still possible to interpret the outcome of the model as a measure of the increase in market power, regardless of what happens when the time t tends to infinity.
4.Being the only non-linear competition model for which the explicit solution is known, it can be used as a useful tool to identify reasonable value of parameters that can be used in more sophisticated models like the one proposed in the following section.
The Model with Prices
In heterogeneous oligopolies market shares are not considered to be the relevant variable and thus the approach presented in the previous section has to be accordingly adjusted. To study directly the behavior prices it is sufficient to abandon the limitation imposed by the artificially imposed connection between Ï’i and hij. It is important to notice that this link has no reason to exist, unless we want to strictly rely on the model based on differential equations that has as a solution exactly the function used to describe the competitive interaction in the ALM. Abandoning this limitation it will be possible to adopt the prices as the main variables. Before describing the model it is necessary to understand the difference between the model proposed here and a classic model of competition. In a classic competition model an increase in the value of the main variable of firm Fi would cause a reduction in the value of other firms main variables; this is not necessarily true with prices. To overcome this problem it is sufficient to require that hi j can be either positive or negative. In case the relation between firms prices is positive, hij will be negative, and vice versa (if the relation is negative, hij will be positive). It is also possible to describe the situation where firms fix their prices independently from each other by equating hij to 0. For this reason the model is still described by the equations (10) in which the parametershij are arbitrary.
Again the equilibrium positions are the solutions of the algebraic system (10), obtained equating to zero the right-hand side of (9). In particular, if n=3, three of these solutions correspond to a monopoly of one firm; three solutions correspond to the presence of two firms and the last three lead to an equilibrium in which the three firms exist. All these solutions are possible provided that the constants hij verify suitable conditions.
We observe that it is possible to find equilibrium positions different from monopoly in which firms coexist on the market without one of them completely prevailing over the others. This kind of prediction seems to be more reasonable and introduces the possibility of running some very important tests. Such an analysis is grounded on a completely different logic form the previous one and is suited only for mergers who raise serious anticompetitive concerns, hence calling for an in depth analysis.
Concluding remarks
Predicting the competitive effect of mergers implies the study of powers competing against each other; this is far from being a problem specific to industrial economics. In this paper I have tried to reconcile the economic approach to the evaluation of mergers with the one employed in biology and other sciences (i.e. Volterra 1927; Rescigno and Richardson 1965; Allen 2007), by showing that the two groups of scholars have unwittingly been studying the two faces of the same coin. On the one hand competition models were being studied without knowing their closed form solution; on the other hand, economists have been studying a function that is exactly the unknown solution of one of the most general competition models. To discover that both groups of scholars have identified, independently from each other, the same path to describe the competitive interaction among different powers is surely very encouraging. It may even be interpreted as a hint that such a path is the correct one. Furthermore, both sides could improve their understanding of the phenomena they are studying once the link is identified, by observing the progresses made on the other side. It might be wiser to turn the coin instead of flipping it.
Acknowledgments
I am grateful for the helpful comments I received from Giovanni Figà Talamanca, Peter Camesasca, and Roberto Pardolesi.
References
Allen, L. (2007), An introduction to mathematical biology, Pearson/Prentice Hall, New Jersey.
Ashenfelter, O. and Hosken, D. (2008), ‘The effect of mergers on consumer prices: evidence from five selected case studies‘ (No. w13859), National Bureau of Economic Research.
Publisher
Baker, J. and Rubinfeld D. (1999), ‘Empirical methods in antitrust litigation: review and critique‘ American Law and Economics Review, 1(1), 386-435.
Publisher – Google scholar
Benkard, C. L., Bodoh-Creed A. and Lazarev J. (2008): ‘Simulating the Dynamic Effects of Horizontal Mergers: U.S. Airlines’, Discussion paper, Stanford University
Budzinski, O. (2004), An Evolutionary Theory of Competition, Discussion Paper, available at
http://ssrn.com/abstract=534862.
Budzinski, O. and Ruhmer, I. (2010), ‘ Merger Simulation in Competition Policy: A Survey‘, Journal of Competition Law and Economics, 6(2), 277-320.
Publisher – Google Scholar
Crooke, P., Froeb, L., Tschantz, S. and Werden, G. J. (1999), ‘Effects of assumed demand form on simulated postmerger equilibria‘, Review of Industrial Organization, 15(3), 205-217.
Publisher – Google Scholar
Epstein, R. J. and Rubinfeld, D. L. (2002), ‘Merger simulation: A simplified approach with new applications ‘, Antitrust Law Journal, 69(3), 883-919.
Farrell, Joseph and Shapiro C. (2010), ‘Antitrust evaluation of horizontal mergers: An economic alternative to market definition’, the BE Journal of Theoretical Economics, 10(1), 1-39
Froeb, L.M. and Werden, G. J. (2008), ‘Unilateral Competitive Effects of Horizontal Mergers’, P. Buccirossi (ed.), Handbook of Antitrust Economics, Cambridge, Mass: MIT Press, 43-104.
Kahneman, D. and Klein, G. (2009), ‘Conditions for intuitive expertise: a failure to disagree‘, American Psychologist, 64(6), 515.
Publisher – Google Scholar
Rescigno, A. and Richardson, I. W. (1967), ‘The struggle for life: I. Two species’, Bulletin of Mathematical Biology, 29(2), 377-388.
Tschantz, S., Crooke, P. and Froeb, L. (2000), ‘Mergers in sealed versus oral auctions‘, International Journal of the Economics of Business, 7(2), 201-212.
Publisher – Google Scholar
Van Bergeijk, P. and Kloosterhuis E. (2005), Modeling European Mergers: Theory, Competition Policy and Case Studies, Edward Elgar Pub.
Volterra, Vito. (1927), ‘Variazioni e fluttuazioni del numero d’individui in specie animali conviventi’, Memorie del R. Comitato Talassografico Italiano, 131, 1-142.
Werden, G. J. and Froeb L.M. (2002), ‘The Antitrust Logit Model for Predicting Unilateral Competitive Effects’, Antitrust Law Journal, 70(1), 257—60.
Werden, G. J. and Froeb, L. M. (1994), ‘The Effects of Mergers in Differentiated Products Industries: Logit Demand and Merger Policy’, Journal of Law, Economics, & Organization, 10(2), 407-426.