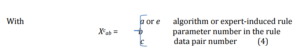Introduction

The financial services sector which includes banking, investment funds, real estate and insurance companies have seen rising demands globally. However, most studies are dedicated on the development and performance of banking sector and almost overlooked another key sector, which is insurance. In Malaysia, the insurance industry which includes two main forms of insurance — conventional and Islamic insurance (Takaful) contributed about 20.1% of the sector’s output in 2011 Nor Zahidi, Nurhisham & Afiq, 2012). Furthermore, Malaysia is also one of the key markets for Islamic insurance which have again achieved double digit growth rates of over 24% last year. 

According to Takaful Act 1984 (Malaysia), Islamic insurance refers to a scheme based on brotherhood, solidarity and mutual assistance which provides for mutual financial aid and assistance to the participants in case of need whereby the participants mutually agree to contribute for that purpose (Bank Negara Malaysia, 2010). Compared to conventional insurance, Islamic insurance applies cooperative principle and the principle of separation between the funds and operations of shareholders. The ownership of the fund and operations are passed to the policyholders whom will act as joint shareholders with the insurance operator. The operator serves as a manager or an entrepreneurial agent for the policyholders.

The policyholders share among them the investment pool’s profits as well as its losses. In Islamic insurance industry, there are two main products offered which are general and family insurance whereas in conventional insurance industry, the products offered are general and life insurance (Muhamad, Mohd Azmi & Raudhah, 2012).

Problem Statement

Despite the continuous positive growth, the Islamic insurance industry continues to suffer from a shortage of human resources with essential expertise. This risk was considered important in both the GCC and South East Asia. The 2012 Takaful Annual Report (Ernst & Young, 2012) highlighted that most senior management at many Takaful operators are from the conventional insurance industry. This poses a human resource risk to the Islamic insurance industry since many are not familiar with the Islamic insurance model. Hence, there is a significant competition for experts in the field. The operators are trying to mitigate the risk by institutionalizing the required knowledge and expertise, and implementing aggressive recruitment strategies as well as offering attractive rewards to support employee retention. 

Additionally, most of us have limited or surface knowledge of what insurance is no matter whether it is conventional or Islamic insurance. Common knowledge is that when a person signs up and pays a certain amount of money to an insurance operator, usually monthly; he or she will have a safety net when certain mishap occurs. The insurance operator will return his or her money plus more depending on the policy(s) he or she signed up for. We have no clue of the actual processes or if the policies we have are adequate for our needs.  Most of the time policyholders rely on the insurance agents to recommend the type of policies suitable for them. They are also influenced by the agents’ sales pitch or good words.

Since insurance agent is the first contact operators have with potential policyholders or prospects.  He or she is responsible to help prospects assess their needs and complete the formalities required to purchase a policy. The operators rely on these agents to obtain less easily quantifiable information about the prospects especially in risk assessment.  Furthermore, in Islamic insurance most of the operators employ the Wakala model. According to the model, the operators earn a service fee which is annually fixed by the operator by deducting from the policyholders’ contribution and/or profit generated from investment funds while the policyholder is the only one being liable for losses. These operators employ agents based on commissions. Agents have to work hard to secure more clients in order to gain higher commissions. Hence, agents need to make fast decisions for potential clients and they will not be able to do this without sound knowledge of the policies and experience.

Agents often employ subjective criteria in evaluating prospects and suggesting suitable policies as well as the coverage distributions. Decision to purchase an insurance policy is not trivial matters as there are many risk factors which may influence the decision. Since the background of prospects varies from one to another, the motivation or likelihood to subscribe to a certain policy also varies. Thus, it is an important aspect for agents to consider prior to proposing a suitable policy for their prospects. Additionally, once a prospect decides to subscribe a policy, he or she needs to carefully decide the distribution of each component within the policy. Consumers usually lack the knowledge to make this decision and most probably will hand over the task to their respective agents. Again, agents will employ subjective criteria, i.e. experience in making the decision. This approach is difficult should the agent is still new to the industry. 

The Proposed Framework

In this study, a decision support tool which applies fuzzy inference system is developed according to the framework illustrated in Figure 1. The framework is adapted from expert system development approach (Kostas, 2004).  There are six main steps involved — identify and analysis the problem, specify functional and operational system requirements, construct the knowledge base, develop system prototype, verify and fine tune the system and implement the system.

Like any system development approach or decision making process, the first step is to identify and analysis the problem in hand specifically the problem faced by the insurance industry stakeholders,  i.e. operators, consumers and investors  in determining or proposing suitable policy which meet the needs and requirements of prospects and existing consumers. The feasibility of FIS to address the problems is also assessed. In the second step, an outline of the general functional and operational system specifications is proposed. Next, the knowledge base is constructed based on the input(s) and output(s) of the FIS components. This knowledge base which is intended for a decision support FIS is the heart of the system. It should have high interpretability, high consistency, high continuity and high completeness (Mamdani & Assilian, 1975). The fuzzy rules contained in the knowledge base are induced from historical dataset. Once the knowledge base is ready, the system prototype is developed. The system is verified and fine tune until it has fulfilled the system requirements specified in the second step. The final step is to implement the system to new cases or proposals.

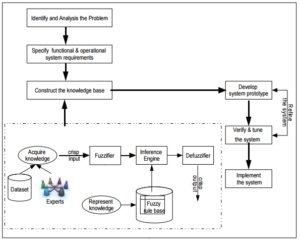
Fig. 1: The Framework

Literature Review

The reasoning process of agents usually takes place in an uncertain and imprecise environment. Therefore, a Fuzzy Inference System (FIS) or also known as Fuzzy Rule-based System is appropriate to alleviate this process. Fuzzy Inference System (FIS) has  been applied to artificial intelligence for representing the knowledge of experts or acquired through learning process (Zadeh, 1965) in various disciplines and industries including insurance. 

De Wit (1982) was the first who worked on applying fuzzy logic to insurance area. His work was to quantify the fuzziness in insurance underwriting. Since then, the fuzzy logic technologies which include fuzzy set theory, fuzzy numbers, fuzzy arithmetic, fuzzy inference systems, fuzzy clustering, fuzzy programming, fuzzy regression, and soft computing have been applied in insurance-related areas. Shapiro (2004) has discussed the major application areas of insurance within 20 years’ time frame (1984-2002). It includes classification, underwriting, projected liabilities, ratemaking and pricing, and asset allocations and investments. 

Past researchers have worked on insurance dataset using different approaches. Lemaire (1990) presents the basic concepts of fuzzy theory in an insurance framework. Fuzzy decision-making procedures are illustrated by a reinsurance application, and the theory of fuzzy numbers is extended to define fuzzy insurance premiums. Stefano (2001) proposed a fuzzy expert system to detect insurance fraud cases.  The system applies a Fuzzy Logic Control (FLC) model which can efficiently evaluate an Index of suspect on each claim, in order to stress fraudulent situation to be investigated by the experts. A system was developed by Aggour et al., (2006) to automise the underwriting of insurance applications using a fuzzy logic rule engine and an evolutionary algorithm to optimize the engine’s performance. A natural language parser was also  used to improve the coverage of the underwriting system. Huang, Lin and Lin (2007) proposed an evaluation model for purchasing life insurance and annuity insurance using analytical hierarchy process (AHP) and fuzzy logic. Four factors are considered as the inputs of the proposed model including age, annual income, educational level and risk preference. They later extended the model for purchasing five types of insurances including life, annuity, health, accident, and investment-oriented insurances. The hybrid model incorporated the Delphi technique into their proposed evaluation model in 2008 (Huang, Lin & Lin, 2008). 

Huang, Lin and Sun (2011) proposed an actuarial model of life insurance for fuzzy markets based on Liu process.  Lien, Ho and Tsai (2011) applied a fuzzy decision tree algorithm to classify the categories of operators’ behavior and conduct the report of abnormal accessing of insurance customer data. The algorithm was found more efficient compared to the C4.5 algorithm. Kumar and Jain (2011) also proposed a fuzzy logic based model for underwriting. However, it is limited to insurers who are diabetic. Ganguly, Basu and Sarkar (2011) addressed the problem of investing money in insurance sector, in order to achieve high return with the help of fuzzy classification.

Even though there are many work reported on applying fuzzy approach to insurance dataset,  there are not many work proposed in the literature to develop decision support tools for selecting insurance policies. Lazim, and Mohd. Nordin (2012) recently proposed the fuzzy rules-based method to classify the likelihoods of purchasing health insurance based on three risk factors which are age, salary and risk of illness. The study has shown that FIS has managed to successfully classify the purchasing likelihoods of employees into three linguistic variables, i.e. high, medium and low. Furthermore, Mohammad Fazle Azeem (2012) highlighted that FIS is very useful to handle expert tasks as well as provide robust method of building systems that may include multiple conflicting, cooperating, and collaborating knowledge.  

Additionally, to the best of our knowledge, none of the past researchers have specifically addressed the need of Islamic insurance industry using fuzzy approaches. Therefore, this study presents a decision support tool using Fuzzy Inference System (FIS) for Islamic insurance agents, prospects, policyholders and operators to support the reasoning or decision making process. The tool will employ human-computer cooperation based on historical dataset. 

Fuzzy Inference System

A fuzzy inference system is able to model human knowledge and reasoning processes without commissioning specific quantitative analyses. It employs fuzzy conditional statement in the form fuzzy IF A THEN B rules, where A and B represent fuzzy sets which are characterized by suitable membership functions (Zadeh, 1965). The basic structure is composed of five main components — a database, the fuzzifier, the inference engine, the defuzzifier, and a fuzzy rule base (as illustrated in Figure 1). 

The database defines the membership functions of the fuzzy sets used in the fuzzy rules. Usually, the database and the fuzzy rule base are defined as the knowledge base. Since FIS refers to a system which uses fuzzy logic and fuzzy set theory to map inputs to output(s) (Zadeh, 1965), the fuzzifier is responsible to transform crisp inputs from the database into degrees of match with linguistic values. After the fuzzification process, the inference engine which is the decision making unit will perform the inference operations on the fuzzy rule base to derive the linguistic values for the intermediate and output linguistic variables. The two main steps in the inference process are aggregation and composition. Aggregation is the process of computing for the values of the IF (antecedent) part of the rules while composition is the process of computing for the values of the THEN (consequent) part of the rules. During aggregation, each condition in the IF part of a rule is assigned a degree of truth based on the degree of membership of the corresponding linguistic term. From here, either the minimum (MIN) or product (PROD) of the degrees of truth of the conditions is usually computed to clip the degree of truth of the IF part. This is assigned as the degree of truth of the THEN part. Once the output linguistic values are available, the defuzzifier produces the final crisp values from the output linguistic values.

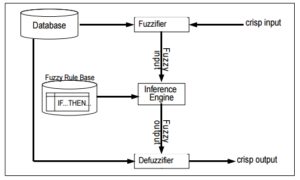
Fig. 2: Fuzzy Inference System (FIS) Components

According to Guillaume (2001), there are two types of FIS — fuzzy expert systems and self-learning FIS. Fuzzy expert system contains fuzzy rule base built from expert knowledge. It focuses on the ability of fuzzy logic to model natural language (Mamdani & Assilian, 1975). This type of FIS allows gradual rules, able to provide a high semantic level and a good generalization capability compared to traditional expert system which is based on classical Boolean logic. However, complex large systems may lead to an insufficient accuracy in the results.  Self-learning FIS is designed from data and include two main processes which are rule generation and rule base optimization (Kostas, 2004). The number of rules induced is highly dependent on the number of variables in the database. The rules will be easier to understand if they are defined by the most prominent variables.  Nevertheless, both types of FIS are able to handle linguistic concepts via universal approximator and able to perform non-linear mappings between input(s) and output(s).

Experiments and Results: Case Study

The knowledge base is constructed based on fuzzy rules induced from a historical database. The historical database consist records of policy holders for three main plan — general and family and group with specific list of policies respectively. According to the operator, the Family Plan is considered as more appealing to clients. Therefore, this study will only focus on the policies under the Family Plan as described in Table 1 which includes 536 records. 

Table 1: Policy Types

A set of linguistic rules are constructed to construct the fuzzy rule base. In a fuzzy inference system, a rule base should be defined based on the characteristics for each variable or feature. A single fuzzy If-Then rule assumes the form of:

IF x is A₁ THEN y is B₂                                                   (2)

Where A₁ and B₂ are linguistic variables defined by fuzzy sets on the ranges (i.e. universe of discourse) X and Yrespectively. The IF-part of the rule ‘x is A₁’ is called the antecedent or premise and the THEN-part of the rule ‘y is B₂’ is called the consequent. The rules are used to describe the importance of the factors on prospects or consumers over the possibility of purchasing insurance policies. The input variables are processed by these rules to generate an appropriate output.

There are three types of rule induction methods, i.e. partitioning, clustering and hybrid. Partitioning method defines a number of fuzzy sets for each variable, which are interpreted as linguistic labels and shared by all rules. The fuzzy sets are tailored for a specific rule. This method allows rules to be generated from data or pre-determined by experts is applied. Clustering method is used to categorize and organize data. It gathers training pairs into homogenous groups and associates a rule to each group. However, the disadvantage of this method is that it generates fuzzy sets which are usually difficult to interpret. Hybrid method integrates many different tools such as neural networks and genetic algorithm. This method is useful for applications which do not require high interpretability and no expert knowledge is available (Ernst & Young, 2012). In this study, the knowledge base is constructed from rules induced from dataset as well as from expert knowledge. Therefore, the partitioning method is most suitable.

The historical database used in this study includes 536 records with 33 variables which includes two categories of information— the demographic data and the policy details. Therefore, it is essential to identify the most influential variables as the input variables. An expert with more than ten years of experience in the industry was involved to identify the rules used as a basis to target their market or approach a prospect. Out of 33 variables, the expert highlighted five demographic variables which are considered most important in the task. The variables are age, gender, marital status,monthly salary and job class. These are the first variables an insurance agent usually looks into before recommending any policy type to a prospect or policyholder.

However, since only one expert was involved and the number of variables may affect the number of rules induced, this study also applies machine learning approach to support the claims of the expert in terms of variables selection. The more variables included, the more rules are induced (Kostas, 2004). Furthermore, the variable selection process is expected to facilitate induction of more compact sets of rules, improve rules interpretability and stability, remove noise and not useful information and ease rule base and parameter optimization processes (Mamdani & Asililian, 1975).

Table 2: Sample Expert-Induced Rules

In this study, the proposed variables i.e. age, gender, marital status, monthly salary and job class are evaluated using a learning scheme available in Weka where the correlation coefficients value is 0.9728.  This indicates a strong positive relationship between the proposed variables. The learning scheme accuracy is evaluated using J48 decision tree algorithm. The accuracy is 0.9091. This supports the expert claim as well. Therefore, the proposed variables are chosen as input and output variables for the proposed fuzzy inference system where Age, JobClass, Gender, Marital Status andSalary data are required inputs for the FIS to propose a suitable policy type.

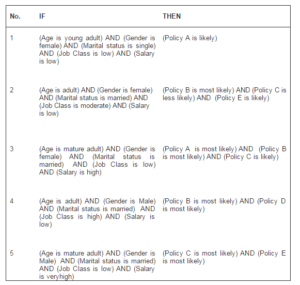
The expert has also listed 21 fuzzy rules based on the five demographic variables. Examples of the induced rules are shown in Table2.
 
The Algorithm 

Wang and Mendel (1992) proposed a partitioning method which limits the number of rules based on the number of training pairs. They proposed a five step procedure which allows new rules to compete with existing rules, thus creating an adaptive rule base. Generally, this method generates complete rules while simultaneously considering all the available variables. The Wang and Mendel algorithm (WMA) identified five input variables- age, gender, marital status, monthly salary and job class. Based on these variables, the Fuzzy Inference System will recommend the single output variable which is policy type. The output variable is policy type. These variables are divided into a number of user defined triangular membership functions. The algorithm induced 54 fuzzy rules based on the dataset.  Examples of the induced rules are as in Table 3.

Table 3: Sample WMA-Induced Rules

Rule Base Completeness and Accuracy

The rules induced from Wang and Mendel algorithm and expert compliments each other. The rule base is considered adequate and complete once rules induced by both parties are combined as one whole fuzzy rule base for our fuzzy inference system. The final rule base consists of 42 rules. In this study, we applied the method proposed by Ketata etal., (2007).  There are two main steps:

• Step 1 : create a combined fuzzy rule base based on both the generated rules and linguistic rules of human experts

• Step 2: determines a mapping from input space to output space based on the combined fuzzy rule base using a deffuzification procedure.
•  

The similarity relations, S(A_ik, A_ij) is defined by Equation (2). The similarity measure between expert-induced rule and WMA-induced rule is defined by Equation (3).S(A_ik, A_ij) = 0 when the fuzzy sets differ in two compared rules differ from one another. 

In this study, we set the minimal threshold for similarity at 60%. Rules with similarity measures above the threshold are merged. This is further shown in Equation (4) below where X refers to input parameters while Y refers to output parameters.

D_e = {(X¹_e1, X¹_e2, X¹_e3, X¹_e4, X¹_en, Y¹_e1),(X²_e1, X²_e2, X²_e3, X²_e4, Y²_e1), (X³_e1, X³_e2, X³_e3, X²_e4,Y³_e1)}

D_a = {(X¹_a1, X¹_a2, X¹_a3, X¹_a4, Y¹_a1),  (X²_a1, X²_a2, X²_a3, X²_a4, Y²_a1) }

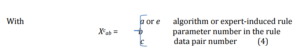
For example, consider rule number 4 from Table 5 and Table 6 as follows. For simplicity, we rename the rules as R_e(expert rule) and R_a (algorithm rule).

R_e:

IF (Age is adult) and (Gender is Male) and (Marital Status is married) and (Job Class is high) and (Salary is high) THEN (policy B is most likely)

R_a:

IF (Age is adult) AND (Gender is Male) AND (Marital status is married) AND (Job Class is high) AND (Salary is low) THEN (Policy B is most likely) AND (Policy D is most likely)

There are six parameters in R_e and seven parameters in R_a. Among these, five of the parameters are induced in both rules. Therefore, using Equation (3), the degree of similarity, d_s between these two rules is 5/7 = 71.43% which is greater than the predefined threshold of 60%.  Hence, these two rules are merged. Based on Ketata et al.,’s (2007) approach, the merger results with this rule.

IF (Age is adult) AND (Gender is Male) AND (Marital status is married) AND (Job Class is high) AND (Salary is low) THEN (Policy B OR Policy D is most likely)

The fuzzy rule base is evaluated base on the accuracy of the rules. This is done by comparing the output of the system with existing records (Mendel, 2001). In this study, error cases which refer to the number of cases where the system output is different from existing record are observed. In this study, the accuracy is calculated at 74.5%. The rule base is considered accurate and acceptable since the number of error cases is less than 30%. 

Conclusions and Future Work

The final rule base is the heart if the fuzzy inference system (FIS). Since there are no current decision support tool which specifically applies FIS and specifically built for Islamic insurance need, this study is hoped to serve as a starting point for future researcher to explore. The fuzzy rules may assist insurance agents in terms of providing effective direct marketing. In other words, recommending the right policy to the right client and eventually securing new policyholders for the insurance operators. The fuzzy rules support new agents’ decision making process by making it possible for agents to approach more prospects in a day. However, the completeness of the rule base is still under study to increase the accuracy and determine the interpretability of the rules. Further study is needed since we also need to consider other cases such as unclassified cases and ambiguity cases. Future work is also needed to enable the rule base to be adaptive to new rules and further give recommendations on the distribution of basic coverage of each policy.

References

Abduh, M., Omar, M. A. & Tarmizi, R. M. (2012). “Measuring the Performance of Insurance Industry in Malaysia: Islamic vis-à-vis Conventional Insurance,” 16th International Congress on Insurance: Mathematics and Economics, 28-30 June 2012, Hong Kong.               
Publisher – Google Scholar  

Abdullah, L. & Abd Rahman, M. N. (2012). “Employee Likelihood of Purchasing Health Insurance Using Fuzzy Inference System,” International Journal of Computer Science Issues, vol. 9(1), no. 2, 112-116, ISSN: 1694-0814.           
Publisher – Google Scholar    

Aggour, K. S., Bonissone, P. P., Cheetham, W. E. & Messmer, R. P. (2006). “Automating the Underwriting of Insurance Applications,” AI Magazine, vol. 27(3), 36-50.
Publisher – Google Scholar

Bank Negara Malaysia. (2010). ‘Laws of Malaysia Act 312, Takaful Act 1984,’ [Online], [Retrieved December 22, 2012], http://www.mifc.com/index.php?ch=134&pg=247&ac=95&bb=428                       
 
DeWit, G. W. (1982). “Underwriting and Uncertainty,” Insurance: Mathematics and Economics, vol. 1, 277-285.
Publisher – Google Scholar
 
Ernst & Young (2012). “The World Takaful Report,” 7th Annual World Takaful Conference (WTC2012), 16-17 April 2012, Dusit Thani Dubai, UAE. [Online], [Retrieved December 22, 2012],http://www.ey.com/Publication/vwLUAssets/The_World_Takaful_Report_2012/$FILE/Ernst%20&%20Young’s%20The%20
World%20Takaful%20Report%202012.pdf   
Publisher                         
 
Ganguly, R., Basu, K. & Sarkar, A. (2011). “Applications of Fuzzy Classification in Insurance Industry: A Fuzzy Logic Based Approaches,” Recent Advances in Intelligent Computational Systems (RAICS), 22-24 September 2011.               
Publisher – Google Scholar               
 
Guillaume, S. (2001). “‘Designing Fuzzy Inference Systems from Data: An Interpretability-Oriented Review,” IEEE Transactions on Fuzzy Systems, Vol. 9, No. 3, 426-433.
Publisher – Google Scholar

Huang, C.- S., Lin, Y.- J. & Lin, C.- C. (2007). “An Evaluation Model for Determining Insurance Policy Using AHP and Fuzzy Logic: Case Studies of Life and Annuity Insurances,” Proceedings of 8th WSEAS International Conference on Fuzzy Systems, vol. 8, 126-131, 19-21 June 2007, Vancouver, Canada.
Publisher – Google Scholar
 
Huang, C.- S., Lin, Y.- J. & Lin, C.- C. (2008). “Determination of Insurance Policy Using a Hybrid Model of AHP, Fuzzy Logic and Delphi Technique: A Case Study,” WSEAS TRANSACTIONS on COMPUTERS, vol. 7(6), 660-669, ISSN: 1109-2750.               
Publisher – Google Scholar             

Huang, Q., Lin, L. & Sun, T. (2011). “Some Actuarial Formula of Life Insurance for Fuzzy Markets,” Applied Mathematics, vol. 2, 1046-1050.
Publisher – Google Scholar
 
Islamic Banking and Takaful Department of Bank Negara Malaysia. (2010). ’20 Years Experience of Malaysian Takaful Industry,’ [Online], [Retrieved December 22, 2012], http://www.mifc.com/publication/p.9.10.pdf
                 
Kaur, A. & Kaur, A. (2012). “Comparison of Mamdani-Type and Sugeno-Type Fuzzy Inference Systems for Air Conditioning System,” International Journal of Soft Computing and Engineering (IJSCE), vol. 2(2), 323-325, ISSN: 2231-2307.               
Publisher
 
Ketata, R., Bellaaj, H., Chtourou, M. & Amer, M. B. (2007). “Adjustment of Membership Functions, Generation and Reduction of Fuzzy Rule Base from Numerical Data,” Malaysian Journal of Computer Science, vol. 20(2), 147-169.   
Publisher – Google Scholar 

Kumar, S. & Jain, H. (2012). “A Fuzzy Logic Based Model for Life Insurance Underwriting When Insurer is Diabetic,”International Journal of Fuzzy Systems and Rough Systems, vol. 5(1), 51-58.   
Publisher – Google Scholar

Lemaire, J. (1990). Fuzzy Insurance. Astin Bulletin, Vol 20, No 1. pg. 33-55, Center for Research on Risk and Insurance, Wharton School of the University of Pennsylvania.               
Publisher – Google Scholar     

Lien, C.- C., Ho, C.- C. & Tsai, Y.- M. (2011). “Applying Fuzzy Decision Tree to Infer Abnormal Accessing of Insurance Customer Data,” Eighth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD). 26-28 July 2011, Shanghai, China.   
Publisher – Google Scholar
               
Mamdani, E. H. & Assilian, S. (1975). “An Experiment in Linguistic Synthesis with a Fuzzy Logic Controller,”International Journal of Man-Machine Studies, vol. 7, 1—13.
Publisher – Google Scholar
 
Mendel, J. (2001). Uncertain Rule-Based Fuzzy Logic System: Introduction and New Directions, Prentice-Hall, Upper Saddle River, New Jersey, ISBN: 0-13-040969-3.   
Publisher – Google Scholar
 
Mohammad Fazle Azeem (2012). Fuzzy Inference System — Theory and Applications, ISBN: 978-953-51-0525-1. In Tech Publications.             
Publisher                           
 
Nor Zahidi Alias, Nurhisham Hussein & Afiq Akmal Mohamad, (2012). “Malaysian Insurance Industry- A Macro Perspective,” Malaysian Rating Corporation Berhad (MARC) Economic Research, vol. ER/008/2012. [Online], [Retrieved December 22, 2012], http://www.marc.com.my/home/userfiles/file/110612_MalaysianInsuranceIndustry_FINAL_WEB.pdf               
Publisher            
 
Shapiro, A. F. (2004). “Fuzzy Logic in Insurance: The First 20 Years,” Journal of Insurance: Mathematics and Economics, vol. 35, 399—424.
Publisher – Google Scholar
 
Stefano, B. & Gisella, F. (2001). “Insurance Fraud Evaluation: A Fuzzy Expert System,” 2001 IEEE International Fuzzy Systems Conference, 2-5December 2001, Melbourne, Australia.               
Publisher – Google Scholar               
 
Syed Moheeb Kamarulzaman. (2007). ‘Lessons from Malaysia Takaful Industry,’ 20th FAIR (Federation of the Afro-Asian Insurers and Reinsurers Conference), 17-20 October 2007, Marrakech, Morocco.             
 
Takagi, T. & Sugeno, M. (1985). “Fuzzy Identification of Systems and its Applications to Modeling and Control,” IEEE Tran. Syst., Man, Cybern., vol. 15, 116—132.   
Publisher – Google Scholar

Wang, L.- X. & Mendel, J. M. (1992). “Generating Fuzzy Rules by Learning from Examples,” IEEE Trans. on Systems, Man and Cybernetics, 22(6):1414—1427.
Publisher – Google Scholar

Zadeh, L. A. (1965). “Fuzzy Sets,” Information and Control Elsevier Science, vol. 8, 338-353, ISSN: 0019-9958.
Publisher – Google Scholar